大学物理实验：等厚干涉的实验结果

【实验概述与思政要素】

由光波的叠加原理可知，当两列振动方向相同、频率相同而相位差保持恒定的单色光叠加后，光的强度在叠加区的分布是不均匀的，而是在有些地方呈现极大，另一些地方呈现极小，这种在叠加区出现的稳定强度分布现象称为光的干涉。

17世纪初，物理学家牛顿在考察肥皂泡及其他薄膜干涉现象时，把一个玻璃三棱镜压在一个曲率已知的透镜上，偶然发现干涉圆环，并对此进行了实验观测和研究。他发现，用一个曲率半径大的凸透镜和一个平面玻璃相接触，用白光照射时，其接触点出现明暗相间的同心彩色圆圈，用单色光照射，则出现明暗相间的单色圆圈。这是由于光的干涉造成的，这种光学现象被称为“牛顿环”。但由于牛顿信奉光的微粒说而未能对其作出正确的解释。

托马斯·杨发现利用透明物质薄片同样可以观察到干涉现象，进而引导他对牛顿环进行研究，他用自己创建的干涉原理解释牛顿环的成因和薄膜的彩色，并第一个近似地测定了7种色的光的波长，从而完全确认了光的周期性，为光的波动理论找到了又一个强有力的证据。

薄膜干涉分为两种，一种称等倾干涉，另一种称为等厚干涉。等厚干涉是由平行光入射到厚度变化均匀、折射率均匀的薄膜上、下表面而形成的干涉条纹。薄膜厚度相同的地方形成同条干涉条纹，故称等厚干涉。牛顿环和楔形平板干涉都属等厚干涉。

干涉现象在科学研究和工业技术上有着广泛的应用。例如在光学检测中，包括对光学元件和光学系统的检查和测试可以利用等厚干涉条纹来测量玻璃板各处的厚度，以及测量照相机镜头的调制传递函数（MTF）等。利用等厚干涉来检测样品表面是否平整的最常见方法是斐索干涉仪，它利用准直平行光在样品表面反射后与入射光发生干涉，从而得到等厚条纹。此外，还可以采用从迈克耳孙干涉仪改进而来的特怀曼-格林干涉仪。特怀曼-格林干涉仪也使用准直平行光源，并由于从迈克耳孙干涉仪改进而来，它可以使两束相干光的光程非常接近，从而相比于斐索干涉仪它对光源的相干长度要求有所降低。如测量光波波长，精确测量微小长度，厚度和角度，检测试件表面的光洁度，研究机械零件内应力的分布以及在半导体技术中测量硅片上氧化层的厚度等。

【实验目的】

①观察光的等厚干涉现象，加深对干涉现象的认识。

②掌握读数显微镜的使用方法，并用牛顿环测量平凸透镜的曲率半径。

③学习用列表法，逐差法和作图法处理实验数据，计算不确定度，并比较实验结果。

【实验原理】

牛顿环装置是由一块曲率半径较大的平凸玻璃透镜，以其凸面放在一块光学玻璃平板（平晶）上构成的，如图4.14.1所示。平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加，若以平行单色光垂直照射到牛顿环装置上，则经空气层上、下表面反射的两光束存在光程差，它们在平凸透镜的凸面相遇后，将发生干涉。从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环（图4.14.2），称为牛顿环。由于同一干涉环上各处的空气层厚度是相同的，因此它属于等厚干涉。

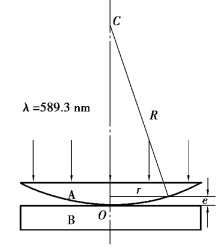
图4.14.1　牛顿环装置

图4.14.2　等厚干涉条纹——牛顿环

由图4.14.1可见，设透镜的曲率半径为R，与接触点O相距为r处空气层的厚度为e，其几何关系式为

R2=(R﹣e)2+r2=R2﹣2Re+e2+r2

由于R≫e，可以略去e2得

设光线是垂直入射的，计算光程差时还要考虑光线从光疏介质向光密介质发生反射时有一相位π的突变，光波从空气射向平玻璃板上反射时会有半波损失，从而带来λ/2的附加程差，所以总程差为

产生暗环的条件是

式中，k=0，1，2，3，…为干涉暗条纹的级数。综合式（4.14.1）、式（4.14.2）和式（4.14.3）可得第k级暗环的半径为

由式（4.14.4）可知，如果单色光源的波长λ已知，测出第m级的暗环半径rm，即可得出平凸透镜的曲率半径R；反之，如果R已知，测出rm后，就可计算出入射单色光波的波长λ。但是用此测量关系式往往误差很大，原因在于凸面和平面不可能是理想的点接触；接触压力会引起局部形变，使接触处成为一个圆形平面，干涉环中心为一暗斑。或者空气间隙层中有了尘埃，附加了光程差，干涉环中心为一亮（或暗）斑，均无法确定环的几何中心。实际测量时，可以通过测量距中心较远的两个暗环的半径rm和rn的平方差来计算曲率半径R。因为

两式相减可得

所以

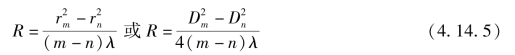
由上式可知，只要测出Dm与Dn（分别为第m与第n条暗环的直径）的值，就能算出R。这样就可避免实验中条纹级数难于确定的困难，利用后一计算式还可克服确定条纹中心位置的困难。

【实验仪器】

牛顿环、钠光灯（λ=589.3nm）、读数显微镜。

读数显微镜及其光路如图4.14.3所示。(https://www.xing528.com)

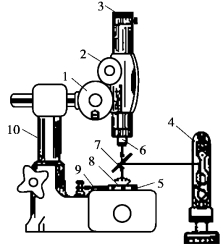
图4.14.3　读数显微镜及光路

1—读数手轮；2—调焦手轮；3—目镜；4—钠光灯；5—平板玻璃；6—物镜；7—透反镜；8—平凸透镜；9—载物台；10—支架

【实验内容】

钠光灯发出波长λ=589.3nm的光由与水平方向成45°角的透反镜（半反射半透射）反射后，垂直入射到平凸透镜上，干涉条纹通过显微镜观察和测量。

（1）用显微镜观察牛顿环

利用显微镜观察物体必须同时满足两个条件：“对准”和“调焦”在被观察的物体上。实验调整、操作应按以下顺序进行：

①照明。调整读数显微镜的位置，使光线射向显微镜物镜下方45°透反镜，并使单色平行光垂直入射到牛顿环装置上。调节透反镜的取向，应使显微镜视野中亮度最大。

②调焦。首先调节目镜直至十字叉丝成像清晰。等厚干涉条纹定域在空气间隙上表面附近，故在观察时，读数显微镜必须对准此面调焦，在调焦过程中，旋转调焦手轮的方向时，必须先使显微镜筒接近平凸透镜，然后缓慢地自下而上进行调焦（自上而下调焦容易损坏物镜和被测标本，为操作规程所不允许），直到能看到清晰的干涉图样，即看到了放大了的牛顿环。

③对准。略微移动牛顿环，对准环中心部位，使显微镜中的十字叉丝将牛顿环大致四等分。如不够清晰可稍加调焦，直至条纹最清晰为止。

（2）测量牛顿环直径

转动显微镜测微鼓轮，使显微镜中十字叉丝由环中心向环左方移动，首先使叉丝的交点先超过第16条暗环，然后退回到第16条暗环，再转动测微鼓轮，使叉丝交点依次对准第15，14，13，…，8，7，6等暗环，记下每次显微镜的位置读数。继续转动测微鼓轮，使镜筒经过暗环中心再读出另一方第6环至第15环的读数。

在整个测量过程中，读数显微镜只可沿同一个方向旋转鼓轮，不能进进退退，以避免测微螺距间隙引起的回程误差。在测量某一条纹的直径时，如果在左侧测的是条纹的外侧位置，而在右侧则应测量的是条纹的内侧位置，此条暗环的直径可认为就等于这两个位置之间的距离。因为实验时主要测量间隔为k个干涉环的两个暗环的直径平方差。为了减少读数误差，应将k值取得大一些，则干涉条纹的相对误差就可减小近10倍。本实验要求测量k=6～15级每一暗环的直径，利用逐差法和作图法分别求取条纹的直径平方差，则可获得较精确的R的实验值。

（3）数据记录

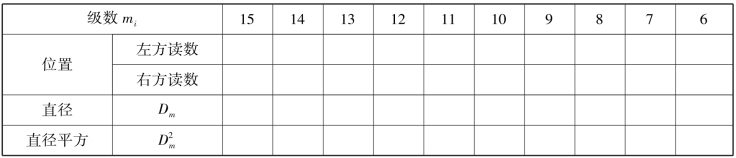
记录实验数据于表4.14.1。

表4.14.1　实验数据记录表

【数据处理】

①利用式（4.14.5）逐差法计算出牛顿环的曲率半径R。

②作图，由斜率4λR计算R。

③分析误差的主要来源。

【注意事项】

①牛顿环仪、透镜和显微镜的光学表面不清洁，要用专门的擦镜纸轻轻揩拭。

②测量显微镜的测微鼓轮在每一次测量过程中只能向一个方向旋转，中途不能反转。

③当用镜筒对待测物聚焦时，为防止损坏显微镜物镜，正确的调节方法是使镜筒移离待测物（即提升镜筒）。

【思考题】

1.牛顿环干涉条纹形成在哪一个面上？产生的条件是什么？

2.牛顿环干涉条纹的中心在什么情况下是暗的？什么情况下是亮的？

3.分析牛顿环相邻暗（或亮）环之间的距离（靠近中心的与靠近边缘的大小）。

4.为什么说读数显微镜测量的是牛顿环的直径，而不是显微镜内被放大了的直径？若改变显微镜的放大倍率，是否影响测量的结果？

5.如何用等厚干涉原理检验光学平面的表面质量？

6.利用读数显微镜测量一微小圆环的内环半径R1、外环半径R2和厚度d，如图4.14.4所示。试说明测量方法和测量步骤。

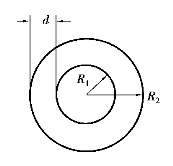
图4.14.4　题6图