直接测量结果的不确定度估算大学物理实验

不确定度的评定方法是一个比较复杂的问题，在多数普通物理实验教学中，为了简便，在进行直接测量的不确定度的合成时，对A类不确定度主要讨论在多次等精度测量条件下，读数分散对应的不确定度，并且用“贝塞尔公式”式（2.2.5）计算A类不确定度，即UA=Sx；对B类不确定度，主要讨论仪器不准确对应的不确定度，即UB=Δ仪，最后将测量（包括后面介绍的间接测量）结果写成标准形式

则总不确定度的合成

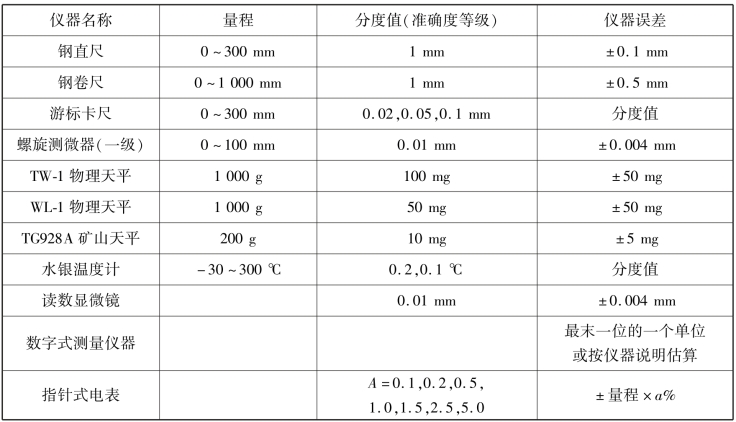
式（2.3.4）是物理实验中常用的不确定度估算公式。常用仪器的仪器误差如表2.3.1所示。

表2.3.1　常用仪器的仪器误差表

为了比较测量结果精确度的高低，常常使用相对不确定度这一概念，其定义为

式中，X为测量值，它可以是单次测量值，也可以是多次测量的算术平均值。这是因为在实际测量过程中，有的被测量无法对其进行重复测量，只能进行单次测量，或测量精度要求不高，只需进行单次测量就可以满足实验要求了。在单次测量中，用单次测量值x测作为被测量的最佳估计值。

在一般情况下，对随机误差很小的测量，可以只估计不确定度的B类分量，用仪器误差Δ仪作为x测的总不确定度，测量结果表示为

如果是多次测量，则总不确定度是合成不确定度式（2.3.4）。因此，实验结果的获得，应包括待测量近似真实值的确定，A、B两类不确定度以及合成不确定度的计算。

应该指出，单次测量的不确定度估算是一个近似或粗略的估算方法。因为测量的随机分布特征是客观存在的，不随测量次数的不同而变化。也不能由此得出结论“单次测量的不确定度小于多次测量的不确定度”的结论。

下面举例说明直接测量不确定度的估算方法。

【例2.1】　用螺旋测微器测量小钢球的直径，8次的测量值d分别为

2.125,2.131,2.121,2.127,2.124,2.126,2.123,2.129mm

螺旋测微器的零点读数d0为0.008mm、最小分度数值为0.01mm，试写出测量结果的标准式。(www.xing528.com)

解：（1）求直径d的算术平均值

（2）修正螺旋测微器的零点误差

（3）计算B类不确定度

螺旋测径器的仪器误差为Δ仪=±0.004（mm）

UB=Δ仪=±0.004（mm）

（4）计算A类不确定度

（5）合成不确定度为

（6）测量结果为

（7）相对不确定度为

当有些不确定度分量的数值很小时，相对而言可以略去不计。在计算合成不确定度中求“方和根”时，若某一平方值小于另一平方值的1/9，则这一项就可以略去不计。这一结论叫作微小误差准则。在进行数据处理时，利用微小误差准则可减少不必要的计算。

不确定度的计算结果，通常约定最多用两位数字表示，且仅当首位为1或2时保留两位。尾数采用“只进不舍”的原则，在运算过程中只需取两位数字计算即可。