生命科学基础研究入门：非参数检验的重要组成部分

前面讨论的方法都是以总体分布为正态分布为前提，对参数进行的检验，属于参数检验方法（parametric test），但是实际上，有些资料并不符合上述条件，甚至分布常常是未知的。本部分所讨论的非参数检验方法（nonparametric test），可以不考虑总体的参数和总体的分布类型，而是对总体的分布或分布位置进行检验。非参数检验是统计分析方法的重要组成部分，它与参数检验共同构成统计推断的基本内容。非参数检验是在总体方差未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数，因而得名为 “非参数”检验。

非参数检验通常适用于以下几种情况：

（1）总体分布为偏态或分布未知的计量资料；

（2）等级资料；

（3）个别数据偏大或数据的某一端无确定的数值，如 “<0.01mg”“>150mg”等，只有一个下限或上限，而没有具体数值；

（4）各组离散程度相差悬殊，即各总体方差不齐。

非参数检验方法的优点是适应性强，但由于损失了部分信息，检验效率有所降低。在资料服从正态分布的前提下，当H0不真时，非参数检验方法不如参数检验方法能灵敏地拒绝H0，换句话说，其犯第二类错误的可能性大于参数检验法。因此，对于适合参数检验的资料，最好还是用参数检验。

（一）配对资料的符号秩和检验

配对资料的符号秩和检验（Wilcoxon signed rank test）是配对设计的非参数检验。

1.检验步骤和基本思想

（1）检验步骤

求出各对数据的差值后依次进行下面的步骤：

①建立假设检验，确定检验水准。

H0：差值的总体中位数为零。

H1：差值的总体中位数不为零。

②确定检验统计量T值（包括编秩次并求秩和）。

编秩：依差值绝对值，从小到大编秩，并按差值的正负，标上正负号。编秩时，在正负号不同的差数中，若有绝对值相等的观测值，则取其平均秩次。对差值为0的对子，舍去不计，相应地总的对子数也要减去其对子数，记为n。分别求正负秩次之和T+与T-，并以绝对值较小者作为统计量T值，如公式（3.20）所示：

秩和：正、负秩和相加应等于总秩和，即T++T-=n（n+1）/2，通过对其计算可以判断T+和T-的计算是否有误。

③确定P值，做出统计推断（查表确定P值范围）。

当n≤25时，可查T界值表，T愈小则P愈小。当T恰为表中的界值时，P值一般都小于表中对应的概率值。

应该注意，当n>25时，无法查T界值表，可按近似正态分布用u检验，其公式为：

相同秩次较多时，采用校正公式：

其中ti为相同秩次的个数。得出u值后，按u界值确定P的范围。

式中0.5是连续校正数。因为T值是不连续的，而u分布是连续的，这种校正影响甚微，可以忽略。

（2）基本思想

如果H0成立，即差值的总体中位数为0，则理论上样本的正负秩和应相等，即T值应为总秩和的一半，即T=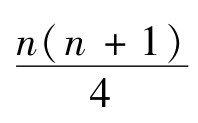。由于存在抽样误差，T应接近T愈小，T与的差距越大，相应的P值就愈小。当P≤α时，拒绝H0。

（二）两样本比较的秩和检验

在t检验一章中，曾介绍了两独立样本均数的比较，但是样本资料要求总体服从正态分布。当此条件不满足时，可采用本节介绍的Wilcoxon Mann-Whitney test方法，其目的是比较两独立样本分别代表的总体分布有无差异。

1.检验步骤与基本思想

（1）检验步骤

①建立假设检验，确定检验水准。

H0：两总体分布相同；(www.xing528.com)

H1：两总体分布不同；

a=0.05。

②确定检验统计量T值（包括编秩次并求秩和）。

编秩：两样本观察值从小到大混合编秩，属不同组的相同观察值取原秩次的平均秩次。

秩和：设n1与n2分别为两样本的含量，规定n1<n2其中为相同秩次的个数。两组合例数N=n1+n2。分别计算两样本含量为n1与n2组对应的秩和T1和T2（两组的秩和合计等于总秩和，即T1+T2=N（N+l）/2，可用于核对），取样本含量小的n1的秩和T1为统计量T值。

③确定P值，做出统计推断。

当n1<10时，查T界值表。T值在表中范围外（包括端点时），P值小于表中对应的概率值，T值在表中范围内，P值大于表中对应的概率值。

当n1与n2超出T界值表的范围时，可按近似正态用u检验：

当相同秩次较多时（如等级资料），采用校正公式：

其中ti为相同轶次的个数。

（2）基本思想

如果H0成立，则两样本来自分布相同的总体，两样本的平均秩次T1/n1与T2/n2应相等或很接近，且都和总体的平均秩次（N+1）/2相差很小。含量为n1样本的秩和T1应在n1（N+l）/2（T值表范围中心为n1（N+1）/2）的左右变化，当T值偏离此值太远，发生的可能性就很小；若偏离出给定a值所确定的范围，即P<a时，拒绝H0。

注：R中Wilcoxon signed rank test及Wilcoxon Mann-Whitney test可用wilcox.test进行分析，wilcox.test的具体运用方法见http：//127.0.0.1：25170/library/stats/html/wilcox.test.html或help（“”）命令调用的帮助文档。

x指数据值的数字向量，y指数据值的可选数字向量需要注意的是，公式界面仅适用于两个样本的测试。如果只x给定，或如果两个x和y中给出并且paired是TRUE，一个Wilcoxon符号空的秩测试的分布x（在一个样本的情况下）或x-y（在成对的两个示例的情况下）是对称 mu的处理。否则，如果两者x并y给出了和paired是FALSE，一个Wilcoxon秩和检验（相当于Mann-Whitney检验：见注）进行。在这种情况下，原假设是的分布，x并且y通过的位置偏移而不同，mu而备选方案是通过其他的位置偏移来使分布不同（并且一侧的备选"greater"是x在的右侧移位y）。默认情况下（如果exact未指定），如果样本包含的有限值少于50个且没有关系，则计算精确的p值。否则，使用正态近似。

（三）多个样本比较的秩和检验

检验的基本步骤：

如果比较的样本多于两个，则可以用本小节的Kruskal-Wallis H检验方法。

设有k个样本，每个样本含量为，总例数。检验的具体步骤如下：

1.建立假设检验，确定检验水准

H0：各抽样总体分布相同；

H1：各抽样总体的分布不同或不全相同；

a=0.05。

2.计算检验统计量

（1）编秩次，将各组数据统一从小到大编秩次，对相等的数值，如果分属不同组时应取平均秩次。

（2）求秩和，分别计算各组的秩和Ti，可用关系式∑Ti=N（N+1）/2检验Ti的计算是否正确。

（3）计算H值：

当相同秩次较多时（如等级资料），采用校正的值，即：

公式中ti为相同秩次的个数。H或Hc近似服从自由度v=k-1的X2分布。按X2的界值表确定P的范围。

注：R中Kruskal-Wallis H检验通过kruskal.test（）实现，其具体运用方法见https：//stat.ethz.ch/R-manual/R-devel/library/stats/html/kruskal.test.html或 help（“”）命令调用的帮助文档。

x指数据值的数字矢量，或数字数据矢量的列表。列表中的非数字元素将被强制并带有警告。g指一个矢量或因子对象，给出对应元素的组x。需要注意的是，kruskal.testx对每个组（样本）中分布的位置参数相同的null进行Kruskal-Wallis秩和检验。另一种选择是它们至少有一个不同。如果x是列表，则将其元素作为要比较的样本，因此必须是数字数据向量。在这种情况下，将 g被忽略，并且可以简单地使用它kruskal.test（x）来执行测试。如果样品尚未包含在列表中，请使用kruskal.test［list（x，...）］。否则，x必须是数字数据向量，并且g必须是与x为的相应元素指定组的长度相同的向量或因子对象x。