方差分析(Analysis of Variance,简称ANOVA),又称 “变异数分析”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验,故又称F检验。对于独立地来自于正态分布总体且总体方差相等的k(k≥3)个样本均数的比较,t检验不再适用,方差分析则是解决上述问题的重要分析方法。方差分析还可用于多因素水平组间效应分析、回归分析等。当然,我们也要注意当方差分析结果有统计学差异时,若要比较均数的大小,需要对多个样本均数进行两两比较,以确定每两两均数之间是否有差异。本节将主要介绍单因素多水平以及两因素多水平组间效应分析的方差分析。
例如,为研究三种新型降血糖药对II型糖尿病的治疗作用,某研究者以统一的纳入标准和排除标准选择了24名未治疗的II型糖尿病患者,按完全随机设计方案将他们分为三组进行双盲临床试验,其中A组8人,B组8人,C组8人,治疗一个月以后分别测量他们的血糖水平,需要比较三种药物的疗效是否有差异,这时就需要使用方差分析。
(一)完全随机设计的方差分析
完全随机设计(completely random design)又称单因素方差分析(one-way analysis of variance,one-way ANOVA),是一种将实验对象随机分配到不同处理组的单因素设计方法。此类设计只考察一个处理因素,通过对该因素不同水平组均值的比较,推断该处理因素不同水平组的均值之间的差异有无统计意义。完全随机设计的数据结构一般形式如表8-4所示,其中k为处理因索的水平数,Xij为处理因素第i水平的第j个观测值,ni(i=l,2,…k)为处理因素第i水平组的观测例数,n为总例数,![]() 为处理因素第i水平组的均数,
为处理因素第i水平组的均数,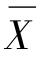 为总均数,
为总均数,![]() 为处理因素第i水平组的方差,S2为全部观测值的方差。
为处理因素第i水平组的方差,S2为全部观测值的方差。
表8-4 完全随机设计方差分析的数据结构
表中,n个观测值彼此不同,可以用方差来反映该变异程度。方差的分子部分为n个观测值的离均差平方和,被称为总变异,记为SST。对此可以作如下分解:
其中,![]() 称为组间变异,是组内均值
称为组间变异,是组内均值![]() 与总均值
与总均值![]() 之差的平方和,记为SSTR,它反映了处理因素各个水平组间的差异,同时也包含了随机误差;
之差的平方和,记为SSTR,它反映了处理因素各个水平组间的差异,同时也包含了随机误差;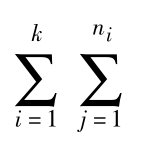
![]() 称为组内变异,是组内各个观测值Xij与本组内均值
称为组内变异,是组内各个观测值Xij与本组内均值![]() 之差的平方和,记为SSE,它反映了各组内样本的随机波动。由上可见,总变异SST、组间变异SSTR和组内变异SSE间满足下式:
之差的平方和,记为SSE,它反映了各组内样本的随机波动。由上可见,总变异SST、组间变异SSTR和组内变异SSE间满足下式:
其中,总变异自由度v=n-1,组间变异自由度vTR=k-1,组内变异自由度vE=(n1-1)+(n2-1)+…+(nk-1)=n-k。对于自由度,同样有:
各变异除以相应自由度得到相应平均变异,即方差,又叫均方。组间均方:
组内(误差)均方:
检验各处理平均值之间有无差异这一假设,可以通过比较MSTR和MSE来实现。MSTR与MSE之比即构成了方差分析的统计量:
由此可以证明,当无效假设H0成立时,这样定义的统计量F服从自由度为(k-1,n-k)的F分布。F值接近1,可认为均值的差异只源于随机波动,而非处理因素作用;F值大于1并且F>Fα(k-1,n-k),P<α,则按a水准拒绝H0,表明有随机波动之外的因素造成了均值的差异。
以上计算过程可用完全随机设计方差分析表进行概括(如表8-5所示)。
表8-5 完全随机设计方差分析表
续 表
(二)随机区组设计的方差分析(https://www.xing528.com)
随机区组设计(randomized block design)又称为配伍组设计,其做法是先将受试对象按条件相同或相近的组成m个区组(或称配伍组),每个区组中有1个受试对象,再将其随机地分到k个处理组中。随机区组设计在m个区组和k个处理水平组构成的mk个格子,每个格子仅一个数据:Xij(i=1,2,3…,k;j=1,2,3,…,m),其方差分析属无重复数据的两因素方差分析(two-way ANOVA),数据结构如表8-6所示。
表8-6 随机区组设计方差分析的数据结构
与完全随机设计方差分析情况类似,总变异SST可分解为:处理A因素的变异SSA、区组B因素的变异SSB以及随机误差SSE。即:
相应的自由度
有关计算式归纳于表8-7的方差分析表中。
表8-7 随机区组设计的方差分析表
续 表
其中,![]() 为A因素第i水平组的均数,
为A因素第i水平组的均数,![]() 为B因素第j区组的均数;n为总观察例数,
为B因素第j区组的均数;n为总观察例数,![]() 为全部观测值总均数,S2为全部观测值的方差。
为全部观测值总均数,S2为全部观测值的方差。
可以看出,与完全随机设计相比,随机区组设计方差分析将总变异分解为三部分,即除了处理组间变异之外,随机区组设计还将区组因素导致的变异也分离出来,从而减少了随机误差,提高了实验准确率。
注:R方差分析aov()的运用可使用help(“aov”)调用该参数的帮助文档,此处不做详述。该命令在单因素、多因素方差分析中均可运用。对双因素方差分析:只需将公式中的x~A改为x~A+B(无交互)或x~A*B(有交互)。
(三)多个样本均数的两两比较
完成方差分析后,我们要么不拒绝H0,推断μ1=μ2=…=μk,要么拒绝H0而接受H1,推断k个均数不全相同。若不拒绝H0,则整个分析便可结束。然而,若接受H1,说明某些组间总体均数不同,就需要进一步作多重比较(multiple comparison),以明确哪些组间有差异。两两比较能否采用t检验呢?如果采用t检验对k个均数进行两两比较,共需比较![]() 次,如k=5,需进行10次比较,假设每次比较所确定的检验水准a=0.05,则每次检验拒绝H0,不犯I类错误的概率为1-0.05=0.95,那么10次检验均不犯I类错误的概率为0.9510=0.5987,而累积犯I类错误的概率为1-0.5987=0.4013。显然,采用前述的t检验进行两两比较是不合理的,这增大了I类错误的概率。
次,如k=5,需进行10次比较,假设每次比较所确定的检验水准a=0.05,则每次检验拒绝H0,不犯I类错误的概率为1-0.05=0.95,那么10次检验均不犯I类错误的概率为0.9510=0.5987,而累积犯I类错误的概率为1-0.5987=0.4013。显然,采用前述的t检验进行两两比较是不合理的,这增大了I类错误的概率。
两两比较的方法很多,SNK(Student-Newman-Keuls)法是较常用的方法之一,其检验统计量为q,故又称为q-检验(Newman-Keuls test)。其计算公式为:
公式中![]() 分别为任意两个对比组的样本均数;分母为两组均值差值的样本标准误差,其中nA、nB为相应的两个对比组的样本例数,MSE为误差均分。
分别为任意两个对比组的样本均数;分母为两组均值差值的样本标准误差,其中nA、nB为相应的两个对比组的样本例数,MSE为误差均分。
注:R多重比较SNK.test的运用,参见http://127.0.0.1:25170/library/agricolae/html/SNK.test.html或键入help(“SNK.test”)后调用的帮助文档。此外,R还提供了LSD.test,Dunnett test(glht,适用于多个试验组与一个对照组的比较),TukeyHSD,等多重比较方法,其中TukeyHSD使用较为广泛。具体使用方法见help("")调用的帮助文档。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




