T检验，亦称student t检验（Student′s t test），主要用于样本含量较小（如n<30），总体标准差σ未知的正态分布。t检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。它与f检验、卡方检验并列。t检验是戈斯特为了观测酿酒质量而发明的，并于1908年在Biometrika上公布。通常需要注意对T检验和秩和检验进行区分，秩和检验一般用于两个非正态总体中所得到的两样本之间的比较，而单样本计量资料多采用T检验，对于不符合正态分布的资料可以采用矫正公式。
一般T检验需要满足样本来自的总体符合正态分布，且其来自的总体符合方差齐性，在进行检验之前总是要确定总体方差是否相等。但也存在有某些特殊情况，当资料服从正态分布，但不服从方差齐性时，通过调整自由度，也能使用T检验。因此，T检验可根据研究设计和资料的性质分为单样本的t检验和两个独立样本t检验，以及存在方差不齐时的t′检验。T检验共同步骤即建立检验假设，确定检验水准，计算检验统计量，确定P值，做出推断结论。
（一）单样本的t检验
单样本的t检验又称单样本均数t检验（one sample t test），适用于样本均数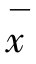
与已知总体均数μ0的比较，其比较目的是检验样本均数
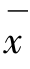所代表的总体均数μ是否与已知总体均数μ0有差别。已知总体均数μ0，一般为正常值、标准值、理论值或经大量观察得到的较稳定的指标值。
单样本t检验用于总体标准差σ未知的资料，其统计量t值按公式（3.1）计算：
其中S为样本标准差，n为样本含量。
例1：以往通过大规模调查，已知某地新生儿出生体重为3.30kg。从该地难产儿中随机抽取35名新生儿作为研究样本，平均出生体重为3.42kg，标准差为0.40kg，问该地难产儿出生体重是否与一般新生儿体重不同？
本例已知总体均数μ0=3.30kg，但总体标准差σ未知，n=35，为小样本，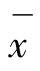
=3.42kg，S=0.40kg，故选用单样本t检验。
1.建立检验假设，确定检验水准
H0：μ=μ0，该地难产儿与一般新生儿平均出生体重相同
H0：μ≠μ0，该地难产儿与一般新生儿平均出生体重不同
a=0.05
2.计算检验统计量
在成立的前提条件下，计算统计量为：
3.确定P值，作出推断结论
本例自由度 v=n-1=35-1=34，查t界值表得t0.05/2.34=2.032。因为t<t0.05/2.34，故P>0.05，表明差异无统计学意义，按a=0.05水准不拒绝H0，即根据现有样本信息，尚不能认为该地难产儿与一般新生儿平均出生体重不同。
（二）配对样本均数t检验
配对样本均数t检验简称配对t检验（paired t test），又称非独立两样本均数t检验，适用于配对设计计量资料均数的比较，其比较目的是检验两相关样本均数所代表的未知总体均数是否有差别。配对设计（paired design）是将受试对象按某些重要特征相近的原则配成对子，每对中的两个个体随机地给予两种处理。应用配对设计可以减少实验的误差和控制非处理因素，提高统计处理的效率。配对设计处理分配方式主要有三种情况：①两个同质受试对象分别接受两种处理，如把同窝、同性别和体重相近的动物配成一对，或把同性別、年龄相近及病情相同的病人配成一对；②同一受试对象或同一标本的两个部分，随机分配接受两种不同处理；③自身对比（self-contrast），即将同一受试对象处理（实验或治疗）前后的结果进行比较，如对高血压患者治疗前后某一生理指标进行比较。前两种情况属于随机对照的配对设计，应采用配对t检验判断两种处理的效果有无差别；后一种自身对比不能随机分配处理，其前后的差别可能是处理因素的作用，也可能是其他因素的影响，因此在实验性研究中应设平行对照。
配对设计的资料具有对子内数据一一对应的特征，研究者应关心对子的效应差值而不是各自的效应值。因此进行配对t检验时，首先应计算各对数据间的差值d，将d作为变量计算均数。配对样本均数t检验的基本原理是假设两种处理的效应相同，理论上差值的总体均数为μd为0，现有样本差值均数不等于0的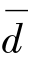
可以来自μd=0的总体，也可以来自μd≠0的总体。因此可将该检验理解为差值样本均数
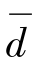与已知总体均数μd（μd=0）比较的单样本t 检验，其检验统计量为：
式中d为每对数据的差值，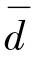
为差值样本的均数，Sd为差值样本的标准差，
为差值样本均数的标准差，即差值样本的标准误，n为配对样本的对子数。
例2：有12名接种卡介苗的儿童，8周后用两批不同的结核菌素，一批是标准结核菌素，一批是新制结核菌素，分別注射在儿童的前臂，两种结核菌素的皮肤浸润反应平均直径（mm）如表8-2所示，问两种结核菌素的反应性是否有差别？
表8-2 12名儿童分别用两种结核菌素的皮肤浸箱反应结果（mm）
续 表
1.建立检验假设，确定检验水准
H0：μ=μ0，两种结核菌素的皮肤浸润反应总体平均直径差异为零
H0：μ≠μ0，两种结核菌素的皮肤浸润反应总体平均直径差异不为零
a=0.05
2.计算检验统计量
先计算差值d及d2，如表6-2第四、五列所示：
本例∑d=39，∑ d2=195
计算差值均数：
计算差值的标准差：
计算差值的标准误：
按公式（3.2）计算，得：
3.确定P值，做出推断结论(www.xing528.com)
自由度v=n-1=12-1=11，查t界值表，得：
t0.05/2.11=2.201，t0.01/2.11=3.106
本例t>t0.01/2.11，P<0.01，差别有统计学意义，拒绝H0，接受H1，可认为两种方法的皮肤浸润反应结果的差别有统计学意义。
（三）两独立样本均数t检验
两独立样本t检验（two independent samples t-test），又称成组t检验，它适用于完全随机设计的两样本均数的比较，其目的是检验两样本所来自总体的均数是否相等。完全随机设计是将受试对象随机地分配到两组中，每组对象分别接受不同的处理，分析比较两组的处理效应。
两独立样本t检验要求两样本所代表的总体服从正态分布，且两样本的总体方差σ12=σ22，即方差齐性（homogeneity of variance）。若两总体方差不齐，可采用t'检验，或进行变量变换及用秩和检验方法处理。两独立样本t检验的检验假设是两总体均数相等，即H0：μ1=μ2，也可表述为μ1-μ2=0，这里可将两样本均数的差值
看成一个统计量，
就是该值的标准误，则在H0条件下两独立样本均数t检验可视为样本
与已知总体均数μ1-μ2=0的单样本t检验，统计量计算公式为：
其中：
称为合并方差（pooled variance），公式（3.5）可用于已知两样本观察值原始资料时的计算，当两样本标准差S1和S2已知时，合并方差Sc 2为：
例3：25例糖尿病患者随机分成两组，甲组单纯用药物治疗，乙组采用药物治疗合并饮食疗法，二个月后测空腹血糖（mmol/L）如表8-3所示，问两种疗法治疗后患者血糖值是否相同？
表8-3 25名糖尿病患者两种疗法治疗后二个月血糖值（mmol/L）
续 表
1.建立检验假设，确定检验水准
H0：μ=μ0，两种疗法治疗后患者血糖值的总体均数相同
H0：μ≠μ0，两种疗法治疗后患者血糖值的总体均数不同
a=0.05
2.计算检验统计量
由原始数据计算得：
代入公式（3.5）和（3.4），得：
按公式（3.3），算得：
3.确定P值，作出推断结论
两独立样本t检验自由度v=n1+n2-2=12+13-2=23；查t界值表，t0.05/2.23=2.069，t0.01/2.23=2.807。由于t0.01/2.23>t>t0.05/2.23，按a=0.05的水准拒绝H0，接受H1，差异有统计学意义，故可认为用两种疗法治疗糖尿病患者，两个月后测得的空腹血糖值均数不同。
有些资料（如抗体滴度的资料）宜用几何均数表示其平均水平。由于这些资料不服从正态分布（常服从对数正态分布），两样本所代表的总体方差也可能不等。当进行几何均数的假设检验时，应先进行变量变换，即将这些观察值X用lgX来代替（即作对数变换），lgX往往近似服从正态分布，相应的两总体方差也可能相等。因为数据变换并未改变两组数据间的相对关系，故可用前述的三种形式的t检验对lgX进行分析。
（四）方差不齐时两样本均数的t′检验
当两总体方差不等（方差不齐）时，两独立样本均数的比较，可采用t′检验，亦称近似之检验（separate variance estimation t-test）。
1.方差齐性检验（详见本章2.2单元）
2.t′检验
t′检验有三种方法，包括Satterthwaite法近似t检验、Welch法近似t检验和Cochran&Cox法近似t检验。Cochran&Cox法是对临界值校正，Satterthwaite法和Welch法是对自由度进行校正。这里主要介绍Satterthwaite法和Cochran&Cox法。t′统计量的计算公式为：
Cochran&Cox法校正临界值
的公式为：
式中v1=n1-1，v2=n2-1，根据校正的临界值，作出推断结论。
Satterthwaite法t'检验的自由度校正公式为：
根据自由度查t界值表，作出推断结论。
目前，Satterthwaite法是统计软件中普遍使用的方法。
此外，应该注意：在 Cochran&Cox 法中，当 n1=n2，v1=v2=v，t′=1，
，v=n-1，此时即使方差不齐，也可用t检验。
注：R语言中t.test的运用可参考https：//stat.ethz.ch/R-manual/library/stats/html/t.test.html或在R中调用help（“t.test”）获取帮助文档。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
