PLC网络系统配置:模拟传输与奈奎斯特定理

1.信号调制解调制

为了克服数字传输的限制，数字数据也可用模拟传输。办法是用数字信号对模拟信号（1000～2000Hz的正弦信号）进行调制。调制后传输。目的站点收到这个调制的模拟信号后，经过解调，可还原为数字信号。有1位、2位、3位等多种二进数调制。

（1）1位二进制数调制

可用0、1分别进行幅度调制、相位调制或频率调制，如图1-24所示。

如图，调幅（Amplitude Modula-tion，AM或Amplitude Shift Keying，ASK），幅度0代表“0”，反之为“1”。调频（Frequency Modulation，FM），也称移频键控（Frequency Shift Keying，FSK），“1”代表频率高，“0”代表频率低。调相（Phase Modulation，PM或Phase Shift Keying，PSK）“0”代表初相位为0°、“1”代表初相位为180°，而信号的频率及幅值不变，这也称绝对调相。此外，还有相对调相，靠相移调制，“1”时初改变，“0”时保持不变。

这3种调制，ASK抗干扰差，PSK最好。而FSK用得较少。

调制的逆过程，即把已调制的信号还原为ON-OFF（0、1）信号，称为解调。调制、解调通常用调制解调器，即Modem实现。

把数字信号做了调制，对通信信道要求就不必太高了。就可以在普通的电话网络中进行长距离传输。这也是常要用到调制解调器的原因。

（2）两位二进制数

即4个信号等级的调制。最方便的是用调相。用同一频率、同一幅值，但初相位不同的4个正弦波，表示两位二进制数的不同值。如用初相位45°表示00，用初相位135°表示01，用初相位225°表示10，用初相位315°表示11。

这样调制一个信号波形也称码元，可传输4个等级的信号，代表2位二进制数据。这样，使用同样的信号传输速率，即波特率，可得到加倍的比特率（二进制信号传输率）。这种技术也称正交相移键控（Quadrature Phase Shift Keying QPSK）。

图1-25a所示的为幅值相同，但相位不同的4个点分别表示两位二进制数的不同值。

图1-24 宽带传输码制

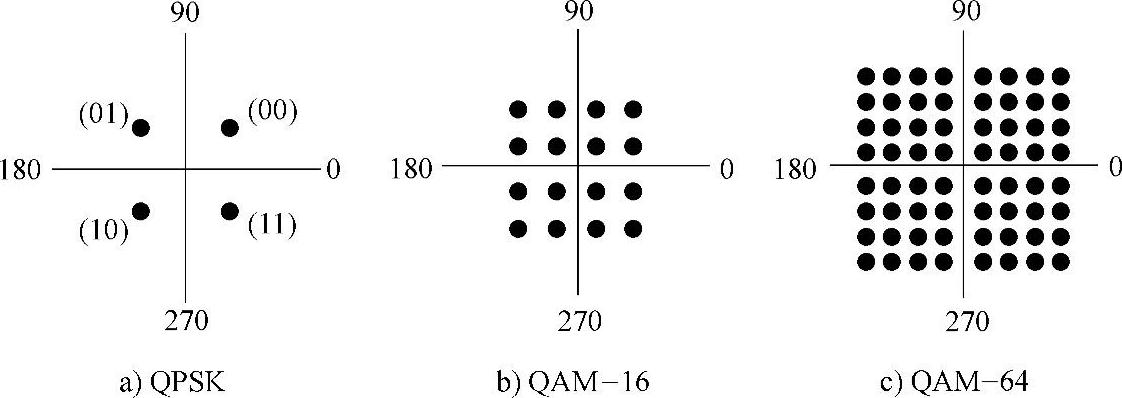
图1-25 16及64等级振幅相位调制组合星座图

（3）n位二进制调制

n位二进制数有2ⁿ值。

如果不仅用多个相位调制，还用多个幅值调制，即正交振幅调制（Quadrature AmplitudeModulation，QAM），可实现更多信号等级。

图1-25b、c所示分别为16（4位二进制数据）及64（6位二进制数据）等级振幅相位调制组合，这个图形也称星座图（Constellation Diagram）。

每个高速调制解调器都有自身的星座图。也只有相同的星座图的Modem才能通信。信号等级太多，可能由于噪声影响而出现信号出错。为此，可增加校验位。如4位二进数，用5位表示。其中一位用作校验。如V.32调制解调器标准，就用了32个星座点，但只传输4个二进制数据。这里多余的一位就是校验位。它的波特率为2400，但比特率为9600。(www.xing528.com)

图1-26b所示为V.32bis的星座图。它用了128个星座点，但只传输6个二进制数据。考虑到校验需要。它的波特率为2400，但比特率为14400。表1-8所示为常用的几种Modem标准，它规定了所采用的调制方式以及所支持的数据传输率。相对图1-25，图1-26旋转了90°，这是为了工程实现的方便。本质上两个图是一样的。

图1-26 V.32 V.32bis Modem星座图

表1-8 常用Modem标准

注：括号中1为校验位。

此外，为了提高Modem的传输速度和有效数据传输率，目前许多Modem都采用数据压缩和差错控制技术。数据压缩指的是发送端的Modem在发送数据以前先将数据进行压缩，而接收端的Modem收到数据后再把数据还原，从而提高了Modem的有效传输速率。

2.最高速率限制

数字传输速率受限制的，模拟传输速率也是受限制的。早在1924年，美国AT＆T公司的工程师奈奎斯特（Henry Nyquist）针对有限带宽、无噪声的信道，提出计算其最大数据传输率的奈奎斯特定理。即

数据传输速率（bit/s）=2Hlog₂V式中，H为信道带宽；V信号的离散等级。例如信道带宽为3kHz，分为两个等级时，传输速率只能为6000bit/s。当然，如果多分等级，则传输速率可相应提高。

然而在实际条件下，信号等级不能无限增加，否则由于干扰而造成相邻等级信号无法区分。所以，实际信号传输速率还要受香农（Shannon）定理限制。即

最大数据传输速率（bit/s）=Hlog₂（1+S/N）式中，H为信道带宽，S/N为信道的信（号与）噪（声之）比。多数情况下，信噪比用分贝（dB）表示。即

信噪比（dB）=10log₁₀S/N

这样如果给出的是dB信道比，那要先换算成S/N后再计算。如普通电话信道，其带宽为3000Hz，信噪比（dB）为30。那么它的最大数据传输速率为

最大数据传输速率（bit/s）=Hlog₂（1+S/N）

=3500log₂（1+1000）

≈35000

这是它的最大传输速率。实际上比它还要低些。

香农公式告诉我们，若要得到无限大的信息传输速率，只有两个办法：要么使用无限大的传输带宽（这显然不可能），要么使信号的信噪比为无限大，即采用没有噪声的传输信道或使用无限大的发送功率（当然这些也都是不可能的）。也就是说，信号的传输速率总是要受限制的。