多元统计分析：实例与SAS实现

我们选取CGSS数据，包括2003年、2005年、2006年、2008年、2010年、2011年、2012年、2013年8次调查数据，在剔除缺失值后保留样本68338个。CGSS2003—2013属于重复横断面调查，关于CGSS的更多介绍详见其官网。我们选择幸福感作为结局变量，选择年龄、年龄平方、教育作为个体层自变量，选择时期和队列作为第二层变量，最后选择时期层面的人均GDP增量作为第二层自变量。当然，具体研究中一般会纳入更多控制变量，我们在此仅选择必要的变量作为操作案例。我们想要探究一下几个问题或假设。第一，居民幸福感的年龄、时期和队列效应具体如何，即居民幸福感随着年龄、时期和队列的推移如何变化。第二，如存在明显的时期效应，根据“伊斯特林悖论（Easterlin Paradox）”^[2]，其是否受经济发展的影响。第三，接受高等教育是否影响居民幸福感的队列变化轨迹。具体变量信息见表14-6。

表14-6　HAPC-CCREM变量基本信息表

注：原始数据来源于《中国统计年鉴2014》和CGSS2003—2013，部分演示思路和数据源于李婷（2018）以及王培刚和姜俊丰（2017）的研究。

首先，我们仅纳入年龄、时期和队列变量以回答第一个问题，设定模型如下。

一层模型：

二层模型：

我们省略数据编码过程，直接演示CCREM的SAS语句。常用的CGSS数据是以SPSS的数据库形式保存的，故首先需要将SPSS格式数据导入SAS，随后运行模型。本节所用数据集名称为exe14＿2。

SAS程序：

proc glimmix data＝exe14＿2 maxopt＝10000；

class period cohort＿group；

model happiness＝age＿c age＿c2/solution cl dist＝normal；

random period cohort＿group/solution；covtest glm/wald；

run；

SAS程序解释：

我们使用广义线性混合模型（glimmix）进行估计，maxopt＝10000定义最大迭代次数不超过10000次，一般情况下迭代几次或几十次就可以使模型达到收敛（下面的案例1中迭代了5次就收敛了）。class语句定义第二层变量，model语句中定义自变量和因变量之间的关系式，这里年龄age＿c是经过中心化处理的（即将原值减去其均值，下文程序语句中的GDP1和edu＿college1也表示经过了中心化处理），因为我们还纳入了年龄的平方项，中心化的处理方式有助于降低一次项和平方项之间的共线性，此外还有助于我们利用图形的方式来呈现APC效应。我们将结局变量happiness视作连续型变量，dist＝normal定义其近似服从正态分布，当然读者也可以将其定义为等级变量（等级变量的分层模型参见第十二章内容）。在random语句后，我们同时纳入时期和队列组变量，二者被视作交叉平行、非嵌套的二层变量。covtest语句表示要求输出协方差检验结果，其方法为glm广义线性模型，并采用wald法进行检验。

SAS结果：

SAS输出结果如下：

图14-13　HAPC模型拟合信息

图14-14　HAPC模型协方差估计结果

图14-15　HAPC模型固定效应估计结果

图14-16　HAPC模型随机效应估计结果

SAS结果解释：

很显然，协方差参数检验结果显示，居民幸福感的时期和队列效应均具有统计学意义，其中具体每个时期点和队列组的幸福感估计值需要看随机效应解的结果。固定效应解的结果显示，居民幸福感的年龄和年龄平方效应也具有统计学意义，即二者之间存在正U形关系（平方项估计值为正值表明抛物线开口向上）。

我们继续回答第二个问题，纳入年龄、时期、队列及人均GDP增量变量，设定模型如下。

一层模型：

二层模型：

SAS程序：

proc glimmix data＝cgss.exe14＿2 maxopt＝10000；

class period cohort＿group；

model happiness＝age＿c age＿c2 GDP1/solution cl dist＝normal；

random period cohort＿group/solution；covtest glm/wald；

run；

SAS结果：

SAS结果输出如下：

图14-17　HAPC模型拟合信息(www.xing528.com)

图14-18　HAPC模型协方差估计结果

图14-19　HAPC模型固定效应估计结果

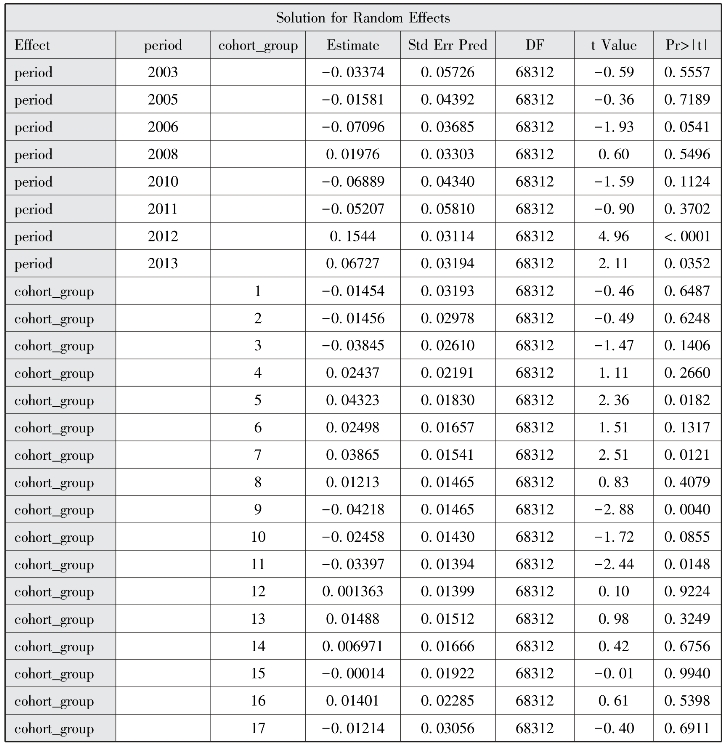
图14-20　HAPC模型随机效应估计结果

SAS结果解释：

以上结果显示，人均GDP增量这一时期特征与居民幸福感之间呈现积极联系，更重要的是，时期项的方差估计值有原来的0.05105下降至现在的0.007194（尽管依然具有统计学意义），表明人均GDP增量在很大程度上解释了居民幸福感的时期变化。

我们继续验证第三个问题，纳入年龄、时期、队列及是否接受过高等教育。设定模型如下：

一层模型：

二层模型：

如公式（14-16）至公式（14-18）所述，在探究队列轨迹的教育差异时，需要设定教育为随机效应β3k，其由不随时间变化的固定效应β3和随队列变化的随机效应c3k组成。

SAS程序：

proc glimmix data＝exe14＿2 maxopt＝10000；

class period cohort＿group；

model happiness＝age＿c age＿c2 edu＿college1/solution cl dist＝normal；

random intercept/subject＝period solution；

random intercept edu＿college1/subject＝cohort＿group solution；

covtest glm/wald；

run；

SAS程序解释：

需要注意的是，在交叉分类的分层设定中，当需要纳入个体随机效应时，研究者需要将两个组水平random语句分开，分别定义时期和队列这两个组水平。

SAS结果：

SAS结果输出如下：

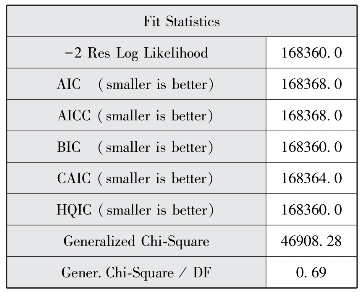
图14-21　HAPC模型拟合信息

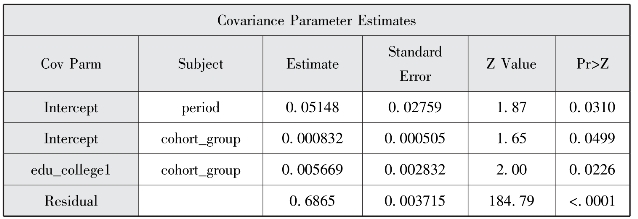
图14-22　HAPC模型协方差估计结果

图14-23　HAPC模型固定效应估计结果

图14-24　HAPC模型随机效应估计结果

SAS结果解释：

随机效应解的结果偏长，我们没有全部展示在这里。从协方差参数估计结果中可知，高等教育变量的随机效应具有统计学意义，也就是说，幸福感得分在接受过和没有接受过高等教育的群体之间的队列变化轨迹是有显著区别的。从固定效应解的结果也可以知道，接受过高等教育的人的幸福感要比没有接受过高等教育的人平均高0.2159分。

至此，我们回答了之前所提出的3个研究问题。进一步的，我们可以用图形的形式来直观展示上述结果，这也是已有相关研究最常用的结果展示方式。我们假设上述三个估计模型分别为模型1、模型2和模型3，由此获得以下年龄、时期和队列效应线。其中，图14-25年龄效应的计算方式为：y＝3.5836－0.00298*agec＋0.00021*age＿c2；图14-26时期效应的计算方式为：yj＝3.5836＋p0j和yj＝3.5792＋p0j；图14-27队列效应的计算方式为：yk＝3.5836＋c0k和

图14-25　中国居民幸福感的年龄效应：基于模型1

图14-26　中国居民幸福感的时期效应：模型1 VS模型2

图14-27　中国居民幸福感的队列效应及其教育差异：模型1 VS模型3

图14-25至图14-27的年龄、时期和队列效应图直观地展示了三个模型的核心结果，并直观解答了一开始提出的三个问题。图14-25显示，幸福感首先随着年龄增长而逐步下降，在50多岁后又会随着年龄增长而上升。图14-26显示，幸福感在2003—2011年期间是逐步上升的，随后略有下降；在控制人均GDP增量后，幸福感时期曲线变得十分平缓，说明幸福感的时期变异在很大程度上可以被这段时期内的高速经济发展所解释。图14-27显示，幸福感随着队列推移不断变化，其中1930年前以及1955—1969年间出生的人拥有较低幸福感，而1930—1954年以及1970年后出生的人拥有较高的幸福感；教育差异分析显示，接受过高等教育的人的幸福感显著较高且具有迥然不同的队列变化轨迹，而未接受过高等教育的人的幸福感队列效应与总体相差不大。