多元统计分析ＳＡＳ实现：年龄-时期-队列模型简介

一般而言，我们经常探究的时间因素可以分解为年龄、时期和队列这三个不同的成分，三者从不同方面影响着人群的各类结局。年龄效应指由生理变化、社会经验积累和/或角色或地位变化所引起的不同年龄组之间的变化。时期效应指随着时期的推移而产生的变化，这种变化同时影响着所有年龄段的人，其通常是由社会、文化或物理环境的变化引起的。队列效应与在相同年代经历出生、结婚等初始事件的人群的变化有关，其反映了在不同时期对不同年龄组有着不同塑造作用的事件或环境的影响（Gleen，2003；Yang＆Land，2013）。也就是说，年龄效应是内力的、个体生理或社会性变化导致的影响，时期效应是外力的、宏观政策或社会事件所带来的瞬时影响，而队列则是内外力的交互作用，是个体在不同年龄阶段经历不同社会事件所带来的累积或延迟效应。

APC模型，顾名思义，旨在同时对上述三种因素进行有效估计。其中，研究者对队列效应尤为关注，以至于有时将APC分析称为队列分析（Yang＆Land，2013）。然而，自Mason等人（1973）于20世纪70年代首次提出APC模型后，该模型的实际应用却一直饱受多重共线问题的困扰，即存在“队列＝时期－年龄”这一线性依赖关系。我们知道，当第三个变量可以表达为前两个变量的线性组合时，研究者就不可能简单地使用常用的回归模型准确估计出三者的效应系数。例如，我国城镇居民1990—2010年的年龄-时期别死亡率数据如表14-1所示。

表14-1　中国城镇居民年龄-时期别死亡率：1990—2010年（单位：每10万人）

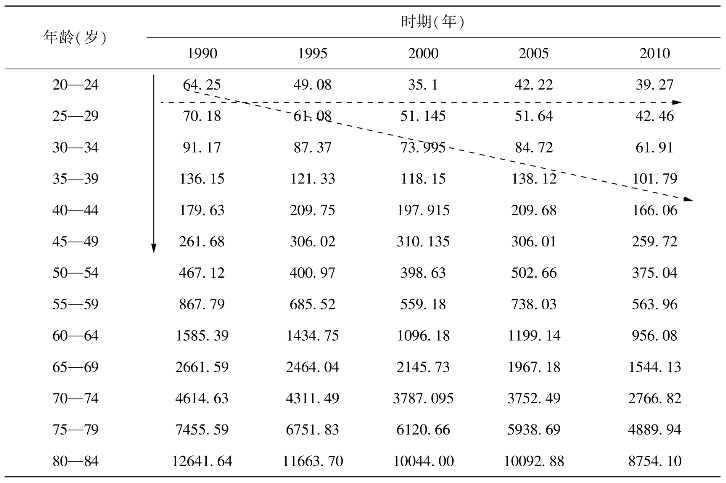
注：原始数据来源于《中国卫生统计年鉴》（1991年、1996年、2001年、2006年、2011年）。数据直接来自陈心广和王培刚（2014）的研究。

在表14-1中，我们以左上角向右下方斜向下画出红虚线箭头，很显然它表示了处于相同出生队列的一群人。例如1990年时处于20—24岁年龄组的人，在1995年就属于25—29岁年龄组，他们均出生于1966—1970年，即属于1966—1970年队列。同样的，在此红虚线箭头上的其他人群均属于该出生队列。从横向视角来看（沿着黑虚线箭头方向，此时年龄组固定不变），时期和队列在统计分析中是完全相同的，即“时期＝队列”；从纵向视角来看（沿着红实线箭头方向，此时时期固定不变），年龄和队列在统计分析中是完全相同的。这类数据结构导致年龄、时期、队列效应之间相互混杂、难以准确识别。无论如何，由于“队列＝时期-年龄”这一线性依赖关系的存在，我们不能轻易得到死亡率的真实年龄、时期、队列效应。

针对上述的年龄-时期别数据，我们可以构建如下代数模型来表示其识别问题：

其中Yij表示结局变量（例如表14-1中的死亡率），μ为截距，agei为第i个年龄组的年龄效应，periodj为第j个时期的时期效应，cohortk为第k个队列组的队列效应，其中k＝Ii＋j（I为年龄组的组数，表14-1中为13），ϵij为与第ij单元格相关的残差。如果以矩阵来表示式14-1，则有：

在公式（14-2）中，X被称为设计矩阵（design matrix），该矩阵对除参照项外的所有项进行编码（包括截距项和三个因素的所有虚拟编码项），其列数为2（I＋J）－3，行数为I×J（J为时期数，表14-1中为5）；出象向量（outcome vector）y的行数也为I×J，b为解向量（solution vector），其行数为2（I＋J）－3，残差向量ϵ有I×J个元素。我们将上述矩阵式两边同时乘以X的转置矩阵X′，可得：(www.xing528.com)

由于一般有E（X′ϵ）＝0，上式可进一步写为：

将等式两边同时乘以X′X的倒数，可以求得解向量b＝（X′X）－1 X′y。然而，由于APC模型中分类编码的三个因素之间存在完全线性依赖关系，使得X矩阵缺少一个秩，即秩亏（rank deficient）为1，因此（X′X）－1实际上是不成立的，因此这种标准方程解法无法得出APC模型的唯一解（O'Brien，2015；Yang＆Land，2013）。在秩亏为1的情况下，APC模型的非唯一解构成一条直线。假设添加约束条件c1，用bc1表示标准方程在该约束条件下的解，那么有：

APC模型之所以会出现线性依赖关系，是因为在零向量（null vector）v生成设计矩阵X的列中存在线性组合，即。由于零向量v由标量（计作s）乘积唯一确定，且APC模型中仅有一个零向量，故有且，故公式（14-5）可以写为：

这表明，bc1＋sv也为标准方程的解，即APC模型的解构成一条直线（O'Brien，2015）^[1]。

APC模型的提出和发展离不开研究者对队列效应的日益关注。队列效应是重要的，不仅仅是因为忽略队列效应会导致年龄和时期效应的有偏估计，还因为队列因素有时对结局确实发挥着根本性的作用。队列效应分析具有坚实的理论依据，即生命历程理论（life course theory）。该理论认为，不同的早年生命经历和体验带来了当前个体结局的分化和差异。该理论尤其强调时间因素的重要性，认为时间既包括生理时间（年龄）和日历时间（时期），也包括历史时间（场景/环境）和社会时间（制度/规范），后两种时间强调了生命早期受生活环境因素的影响（Elder，1974，1998）。例如，在生命历程理论框架下，个体死亡风险既包含了当前即时性的风险暴露，也包含了从出生到当前的累积性风险暴露（累积/滞后效应），且在不同人生阶段/年龄阶段下经历这种早期风险暴露会带来不同的死亡风险（关键期/敏感期效应）。

在APC模型半个世纪的发展史中，围绕如何解决三者间的完全线性依赖问题产生了诸多极具启发意义的估计方法，使APC模型的理论与应用研究充满活力与魅力。APC模型既可以用于分析宏观/聚合数据，也可以用于分析个体微观数据。在接下来的几个小节里，我们尽量不去展开介绍APC模型晦涩难懂的数学原理，而是着重介绍APC模型在聚合数据中的应用方法，包括一般约束估计、内源估计及因素特征估计三种。最后，我们再对一种常用于分析微观数据的APC模型——分层APC-交叉分类随机效应模型进行简单介绍。针对聚合数据分析，我们使用前面提到的中国城镇居民死亡率数据进行案例演示；针对微观数据分析，我们使用中国综合社会调查（Chinese General Social Survey，CGSS）中的居民幸福感数据进行案例演示。