多元统计分析与ＳＡＳ实现：发展模型特点解析

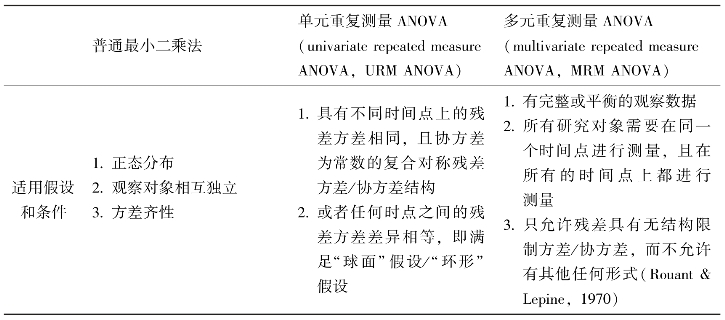
纵向数据具有分级结构，即研究对象的重复测量嵌套于个体中。我们可以将研究对象在各时点的测量看作水平1单位，研究对象则看作水平2单位，这样就可以应用多层模型来分析纵向数据。应用于纵向数据的多层模型也称为发展模型。对纵向数据进行统计分析时，需要能处理个体内同质性（即观察的个体内相关），个体间异质性，非常数方差，以及由失访造成的非平衡数据等问题。传统的分析方法由于自身方法的假设和限定不能很好地处理纵向数据，如表13-3所示。

表13-3　传统分析方法的比较

续表

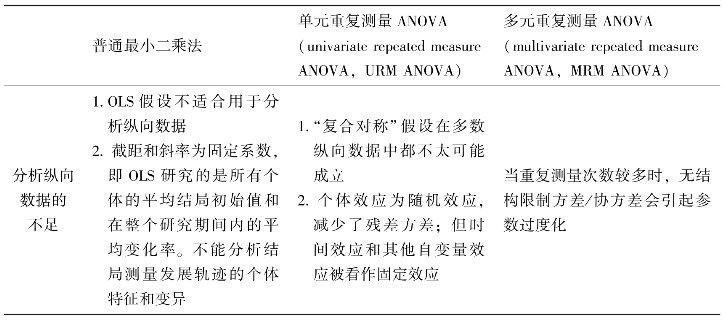
如上表所列，与传统模型相比较，发展模型的优点有以下几点。

第一，在随机缺失（Jos，2002）的前提下，发展模型具有处理非平衡数据和不完整数据的能力，可在最大似然或限制性最大似然的基础上，利用全部可以利用的数据进行模型估计。(www.xing528.com)

第二，发展模型能够处理各研究对象重复测量次数不等，重复测量间隔时间不等的问题。

第三，发展模型既不需要研究对象内的观察值相互独立，也不受某些限制性假设（如“复合对称”假设）的制约。该方法既可以从研究对象个体内变异的角度，也可以从研究个体间变异的角度，或同时从以上两个角度出发来分析纵向数据。

从个体变异的角度出发，模型假设观察对象在不同时间的观察值相关，是由非测量因素产生的对象变异引起的。因此，在模型中设定随机回归系数，如随机截距反映个体结局测量值的不同初始水平，用时间变量的随机斜率反映个体结局测量随时间的变化率，从而引入个体特定效应来处理对象间异质性的问题。

从对象内变异角度出发，可在构建模型时通过设定一个适当的残差方差/协方差结构来处理数据的序列相关。如果用以上两种途经中的任何一种（即分别在模型引入随机回归系数或设定残差方差/协方差结构）仍不足以解释结局测量方差，我们可以构建一个全混合效应线性模型，即在随机回归系数纳入模型的同时，又在模型中设定适当的残差方差/协方差结构。

第四，发展模型能够非常容易地在模型中纳入时间变化协变量，如随访时观察对象婚姻状况、经济收入、行为测量及健康状况等。