混合模型中的全模型及其参数估计

在混合模型的基础上，进一步在随机系数中纳入水平2解释变量，该模型称之为全模型（full model）。需要注意的是，模型中的水平1解释变量既有随机效应又有固定效应，并形成了两水平多层模型的形式。经过模拟调适，我们最终选择了模型拟合效果和模型解释能力较强的模型，模型设定如下：

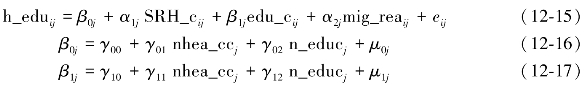
公式（12-15）至公式（12-17）中，系数β0j和β1j具有随机效应，而α1j、α2j被设定为固定效应。随机系数β0j和β1j被定义为2个社区层面解释变量社区健康教育种类、健康宣传栏更新次数的线性函数。γ00表示控制社区层面变量后，水平2变量所有回归截距的条件均值。γ01、γ02表示社区特征：宣传栏更新次数、社区健康教育种类对流动人口接受健康教育种类的影响。γ10表示控制社区解释变量后教育程度对流动人口接受社区健康教育种类影响的平均值。γ11、γ12分别表示健康宣传栏更新次数和社区健康教育种类对健康教育回归斜率的影响。将上式模型组合，可得到以下组合模型：

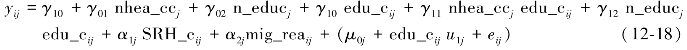
该组合模型有两个组成部分：第一部分为固定效应部分，所有的回归系数γ和α；第二部分随机效应为模型的残差项μ0j、edu＿cij u1j和eij，它们均为无法观测到的潜在变量，这一残差项的结构比常规线性模型的残差项复杂得多。组合模型同时形成了跨层交互作用（cross-level interaction）γ11和γ12。跨层交互作用意味着不同宏观水平变量对个体的作用不一致。以教育程度和健康宣传栏更新次数的跨层交互作用为例，可以解释为健康宣传栏更新次数对小学及以下流动人口接受社区健康教育的影响为γ01，对高中及以上流动人口接受社区健康教育的影响为γ01＋γ11。在构建交互作用之前，需要通过中心化降低变量间多重共线性，提高模型的估计效率。当交互作用显著时，无论主效应是否显著，均应该保留在模型中，否则变量的具体效应将无法解释（王济川等，2008）。为更直观地理解跨层交互项，本部分还绘制了交互作用的折线图。

以上模型均采用reml法进行估计，本小节进一步运用SAS中的ml估计法和reml估计法进行估计效果的差别比较。尽管多层模型可以简单地视为一种“回归的回归”，但是实际上第二层模型中的βij需要通过模型估计得到。代入第一层模型所得到的组合模型包含微观和宏观两个层次上的随机误差，这一复合残差结构使得模型估计变成了一个复杂的问题，在过去制约了多层模型的应用。随着统计方法和算法在20世纪80年代的突破性发展，诸如MLE算法、Bayes方法都被用来对多层线性模型进行求解。本小节主要涉及不同类型估计方法的应用条件，具体的数理推导过程参考相关书籍或文章（Mason，et al.，1987；Raudenbush，et al.，2002）。

在SAS程序中，多层模型采用最大似然估计（maximum likelihood estimation，MLE）方法来估计模型的方差和协方差。最大似然估计是一种迭代估计，随着样本量的增加，最大似然估计逐渐向无偏估计趋近并且具有最小方差，模型估计更可能接近参数的真值。在具体应用中，最大似然估计方法又分为完全最大似然法（full maximum likelihood，FML）和限制性最大似然法（restricted maximum likelihood，REML）。REML对方差成分的估计对固定效应的不确定性进行了调整，但FML却并没有。REML和FML估计的差异可通过如下公式表示：

其中，eij为残差项，i＝1，2，…，n，服从均数为0，方差为常数σ2的正态分布。Q为解释变量的数量。当社区内流动人口数量偏少时，且Q值较大时，使用FML法估计σ2会导致严重的偏差，导致假设检验过于显著。此外，经验贝叶斯（empirical bayes estimator）、迭代广义最小二乘法（iterative generalized least squares，IGLS）、限制性迭代广义最小二乘法（restricted iterative generalized least squares，RIGLS）等也是对多层线性模型进行参数估计的重要方法。目前，实现多层模型分析的主流软件有HLM、LISREL、MLwin、Mplus等专门软件，也包括诸如R、SPSS、Stata、SAS等通用软件（谢宇，2013）。但需要注意的是，不同软件在默认估计方法的选择上存在不同的偏好，比如在Stata、SAS和HLM中，REML估计是默认选择；而MLwin则主要应用IGLS和RIGLS进行参数估计。因此，采用不同软件进行模型参数估计时，可能会在结果上存在一定差异。

SAS程序：

采用method＝reml选项进行reml估计的sas程序如下：

proc mixed data＝mig＿c method＝reml covtest；

class c6；

model h＿edu＝edu＿c｜n＿educ edu＿c｜nhea＿cc SRH＿c mig＿reac

/solution ddfm＝bw notest；

random int edu＿c/subject＝c6；

run；

采用method＝ml选项进行ml估计的SAS程序如下：

proc mixed data＝mig＿c method＝ml covtest；

class c6；

model h＿edu＝edu＿c｜n＿educ edu＿c｜nhea＿cc SRH＿c mig＿reac

/solution ddfm＝bw notest；

random int edu＿c/subject＝c6；

run；

采用proc glimmix选项进行reml估计的SAS程序：

proc glimmix data＝mig＿c；

class c6；

model h＿edu＝edu＿c｜n＿educ edu＿c｜nhea＿cc SRH＿c mig＿reac

/solution ddfm＝bw；

random int edu＿c/subject＝c6；

covtest；

run；

采用proc glimmix绘制交互作用折线图的SAS程序如下：

proc glimmix data＝mig＿c；

class c6 education n＿edu nhea＿c；

model h＿edu＝education｜n＿edu education｜nhea＿c SRH＿c mig＿reac；

random int edu＿c/subject＝c6；

lsmeans education*nhea＿c/plot＝meanplot(sliceby＝education join)；

lsmeans education*n＿edu/plot＝meanplot(sliceby＝education join)；(www.xing528.com)

run；

SAS程序解释：

程序进一步将三个水平1变量纳入random语句后，｜的作用等效于在模型中加入主效应和交互项，例如，h＿edu＝edu＿c｜n＿educ等效于h＿edu＝edu＿c、n＿educ和edu＿c*n＿educ。本部分进一步采用proc mixed程序中的method＝ml和reml选项，分别进行REML和FML估计。proc glimmix程序也能运行多层线性模型，本小节将通过proc glimmix程序进一步运行相同模型。我们省略了proc glimmix中的method＝选项，其默认选项为reml。最后，lsmeans将被运用用于比较不同组别均值大小并画出相应折线图。

SAS结果：

采用method＝reml选项部分运行结果如下：

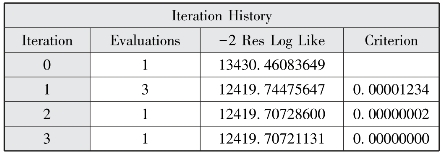
图12-22　迭代历史

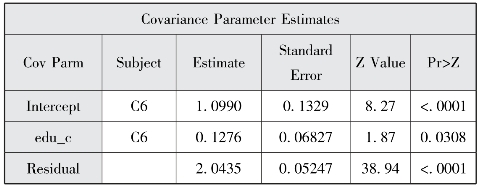
图12-23　协方差参数

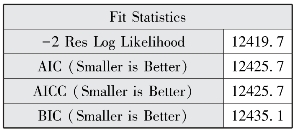
图12-24　模型拟合

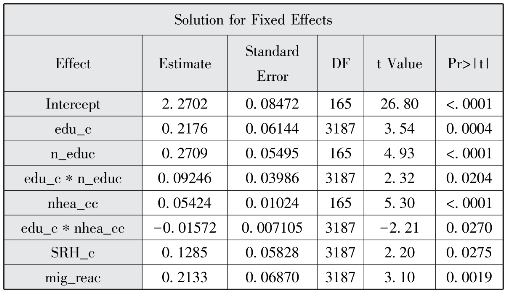
图12-25　固定效应估计

采用method＝ml选项部分运行结果如下：

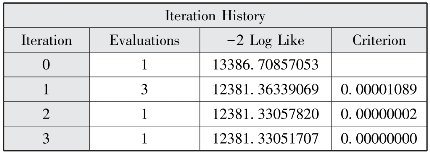
图12-26　迭代历史

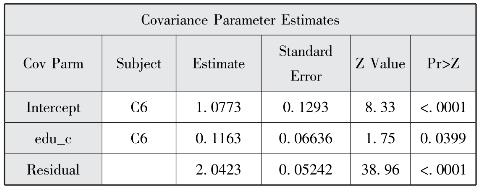
图12-27　协方差参数估计

图12-28　模型拟合

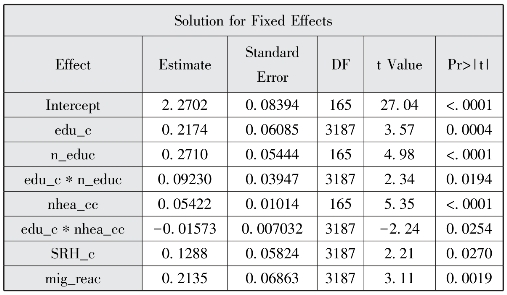
图12-29　固定效应估计

采用proc glimmix选项的部分运行结果如下：

图12-30　迭代历史

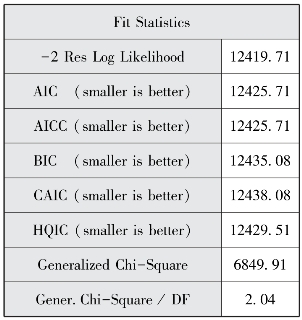
图12-31　模型拟合

图12-32　协方差估计

图12-33　协方差参数估计

采用proc glimmix中lsmeans语句绘制交互作用折线图的部分结果如下：

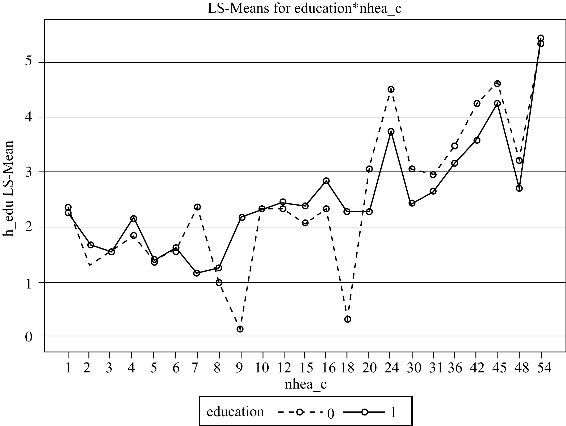
图12-34　不同健康宣传栏次数的社区中不同教育程度流动人口接收健康教育种类均值的折线图

SAS结果解释：

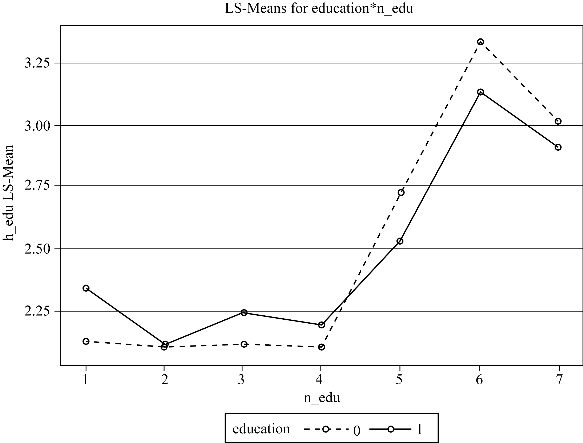
图12-35　不同健康教育种类的社区中不同教育程度流动人口接受健康教育种类均值的折线图

以上程序的结果相似，此处我们主要对method＝reml的结果进行解释，图12-22表明模型评估经过3个迭代后就成功收敛了。图12-24报告了AIC、AICC和BIC三个信息标准值小于纳入水平1协变量的随机截距模型，说明纳入跨层交互项后的模型拟合效果较好。图12-23报告了水平1截距方差和斜率残差方差估计，随机方差的p均小于0.05，说明教育程度及截距项均为随机效应。图12-25显示了固定效应估计结果、流动时间、社区类型以及流动时间和社区类型的交互项均具有统计学意义。教育程度与社区宣传栏更新次数对流动人口接受健康教育种类的跨层交互作用为－0.0157，p＝0.0270，具有统计学意义，说明健康宣传栏更新次数较多的社区对更高学历的流动人口的正面效应减少，由于低学历人群往往需要更多健康教育，反映出通过健康宣传栏进行健康教育的公平性较好。教育程度与社区健康教育种类对流动人口接受健康教育种类的跨层交互效应为0.0925，p＝0.0204水平上具有统计学意义，说明健康教育种类更多的社区对学历更高的流动人口的正面影响增加，这可能是由于社区往往对选择更高学历的流动人口进行健康教育，社区健康教育种类对健康教育的公平性降低。为更详细地展示交互作用，本部分采用proc glimmix选项进行最小二乘均值比较，图12-34显示不同健康宣传栏次数的社区中不同教育程度流动人口接受健康教育种类均值的折线图，健康宣传栏更新次数在20次以上时，学历较低的流动人口能在健康资源较低的社区获得相对更多的健康教育，而在8～18次则高学历流动人口接受的健康教育种类更高；图12-35显示不同健康教育种类的社区中不同教育程度流动人口接受健康教育种类均值的折线图，社区健康教育种类大于5种时，学历较高的流动人口接受健康教育种类较多，而小于5种时结果则正好相反。method＝ml和reml两个选项的差别主要是标准误计算结果的差异，运用reml法计算的标准误调整了解释变量的数量，因而计算的标准误更大。采用proc mixed和proc glimmix程序的估计结果非常一致。