多元统计分析中的混合模型与ＳＡＳ实现

如果随机系数模型中既存在随机效应，又存在固定效应，则被称之为混合模型。混合模型构建如下：

该模型将流动人口个体层面变量健康自评、健康教育和流动原因均进行了总均数中心化处理，健康自评和流动原因被设定为固定效应，教育程度被设定为随机效应，但在社区层面未纳入解释变量。

在运行分层模型之前，需要了解多层模型的特定假设。由于混合模型残差结构相对简单而全面，本章将以混合模型为例说明分层模型的模型假设。普通线性回归模型仅有一个残差eij，且要求呈正态分布。与OLS回归不同，多层线性模型存在多个残差，被称之为复合残差结构。一般将水平2残差的方差/协方差矩阵称为G矩阵，而将水平1残差的方差/协方差矩阵称为R矩阵，具体公式可参见相关书籍（王济川等；2008）。本案例的混合模型中，有水平2残差μ0j、μ1j和水平1残差eij。模型假设水平1残差eij符合正态分布（normal distribution），且水平2残差符合多元正态分布（multivariate normal distribution）；水平1残差和水平2残差相互独立，但水平2残差之间可以存在相关关系，即σu01可以不等于0。相应公式表示为：

σu0表示水平1截距的无条件方差，σu1表示斜率的无条件方差，σu01表示水平1截距和斜率之间的无条件协方差。采用分层模型意味着其随机效应σu0和σu1的数值均不为0，若σu0＝0和σu1＝0，意味着流动人口接受健康教育种类在各个社区的回归线的斜率和截距大致相等，则可以取消随机项中的u0j和u1j，而采用OLS回归。分层线性模型要求因变量与解释变量呈线性关系，但不要求满足独立性和方差齐性。因为分层模型中相同社区的流动人口接受健康教育往往存在相关性，且由于不同社区间流动人口个体变异的差异性，不同社区间的方差往往存在差别。

混合模型的SAS程序及结果如下。

SAS程序：

proc mixed data＝mig＿c method＝reml covtest；

class c6；

model h＿edu＝SRH＿c edu＿c mig＿reac

/solution ddfm＝bw notest；

random int education＿c/subject＝c6；

run；

为进行结果对比，本部分还进行了线性回归，相应SAS程序如下。

proc reg data＝mig＿c；(www.xing528.com)

model h＿edu＝SRH＿c edu＿c mig＿reac；

run；

SAS结果：

SAS结果输出如下：

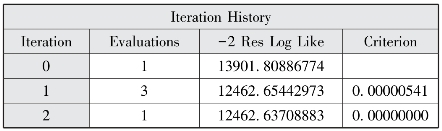
图12-18　迭代历史

图12-19　协方差参数估计

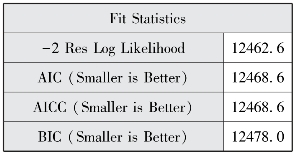
图12-20　模型拟合

图12-21　固定效应估计

SAS结果解释：

混合模型的结果和随机系数模型的结果类似。图12-18表明模型评估经过2个迭代后就成功收敛了。图12-20报告了AIC、AICC和BIC三个信息标准值和－2LL，其AIC、AICC和BIC较随机系数模型略微减少，但－2LL相对增大，说明将健康自评和流动原因回归系数设为固定效应后，模型的拟合程度与随机系数模型接近。图12-19估计部分报告了水平1随机截距方差和随机斜率残差方差估计，教育程度的水平2残差方差的p值小于0.05，说明教育程度的回归系数为随机效应。图12-21显示健康自评每增加一个等级，其接受健康教育的种类就增加0.1292种；高中及以上流动人口较初中及以下流动人口接受健康教育种类多0.2157种；务工经商流动人口较非务工经商接受健康教育多0.2119种。