随机截距模型中的层1协变量分析+SAS实现

若在随机截距模型中纳入水平1控制变量，则将其称之为纳入水平1协变量的随机截距模型。该模型能在控制水平1变量效应的背景下更精确地估计宏观层面变量的效应，且能通过减少水平1残差方差而提高宏观变量的估计精度和假设检验功效。在随机截距模型基础上，进一步加入流动人口健康自评、教育程度和流动原因三个水平1控制变量，模型建构如下：

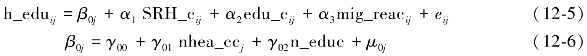
模型的水平1变量健康自评、教育程度和流动原因均进行了中心化处理，且被设定为固定效应。因此，β0j代表控制了健康自评、教育程度和流动原因后调整的均值。那么包括水平1协变量的随机截距模型与随机截距模型的模型拟合优劣如何？这就涉及模型比较的问题。

模型比较可以分为两类，一类为嵌套模型的比较，另一类为非嵌套模型的比较。嵌套模型是指一个模型是另一个模型的亚模型（sub-model）。最大似然估计会产生似然值估计量，将似然估计量取对数并乘以－2就得到离差－2LL（Willian，et al.，2011）。似然比检验（LR test）可用于嵌套模型的模型比较，其原理是通过两模型的－2LL差值进行统计检验。例如，模型（12-3）和模型（12-4）包含2个社区解释变量（社区健康教育种类、健康宣传栏更新次数）和1个随机系数（μ0j）。公式（12-5）和公式（12-6）是包含2个两个相同解释变量（社区健康教育种类、健康宣传栏更新次数）和相同随机效应（μ0j）以及3个额外水平1解释变量（教育程度、健康自评、流动原因）的替代模型。模型（12-3）和模型（12-4）的偏差统计量为DA＝－2 LLA，模型（12-5）和模型（12-6）偏差统计量为：DB＝－2 LLB，则两模型的偏差计量之差为：

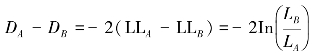
偏差统计量的分布近似卡方分布，其自由度为两模型的参数数目之差（此例中df＝3）。也可通过AIC、AICC、BIC等指标进行嵌套模型和非嵌套模型的模型比较，该类指标数值越小，说明模型的拟合效果越好，AIC、AICC和BIC均可通过－2LL进一步计算可以得到：

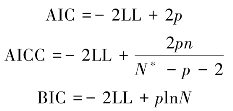
其中，p为模型中参数的总量，而N为水平1样本量；当N≥p＋2，N*＝N；当N＜p＋2，N*＝p＋2。

我们进一步在model右侧纳入宏观变量健康教育宣传栏数量以及水平1控制变量，水平1协变量随机截距模型的SAS程序及结果如下。

SAS程序：

proc mixed data＝mig＿c method＝reml covtest；

class c6；

model h＿edu＝nhea＿cc SRH＿c edu＿c mig＿reac

/solution ddfm＝bw notest；

random int/subject＝c6；(www.xing528.com)

run；

SAS结果：

SAS结果输出如下：

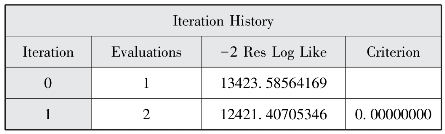
图12-10　迭代历史

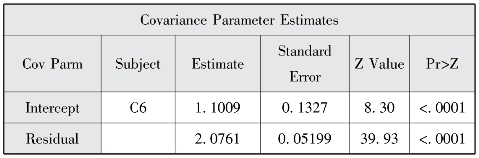
图12-11　协方差参数估计

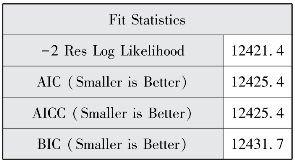
图12-12　模型拟合参数

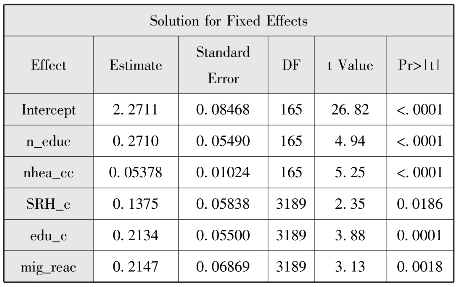
图12-13　固定效应估计

SAS结果解释：

图12-10表明模型评估经过1个迭代后就成功收敛了。图12-12报告了AIC、AICC和BIC三个信息标准值和－2LL较随机截距模型均有所减少。控制协变量后，组内相关系数变为条件组内相关系数。纳入水平1变量不仅可以解释水平1变异且可以解释宏观层面的变异，图12-11报告了水平1随机截距方差（，p＜0.001）和水平1残差方差（，p＜0.001）估计，较随机截距模型分别减少了0.0132和0.0179。在控制个体层面变量后，图12-13显示健康教育宣传栏更新每增加1次，健康教育的种类就增加0.0538种；社区开展的健康教育种类每增加1种，流动人口接受健康教育的种类就增加0.2710种，略大于随机截距模型的结果。