随机截距模型实现-多元统计分析与ＳＡＳ实现

由于空模型显示结局变量存在组间变异，为研究宏观因素对解释变量的影响，需要进一步纳入宏观层面变量，以解释宏观层面的差异。由于仅模型截距被设定为随机效应，我们将其称为随机截距模型（random-intercept model）。在空模型基础上进一步加入2个社区层面解释变量社区健康种类和健康宣传栏更新次数用于解释流动人口接受健康教育种类均值的随机变异，随机截距模型建构如下：

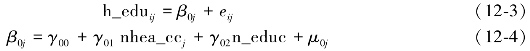
与空模型中相比，此处的μ0j有了新的含义。空模型中的μ0j是指社区j的流动人口接受健康教育平均值与总平均值的离差（随机误差），而随机截距模型中μ0j是指社区层面流动人口接受社区健康教育均值的实际观测值与预测值之差，即残差。β0j为流动人口接受健康教育种类的粗均值。该模型中的社区层面的2个变量均进行了中心化，γ00代表控制社区层面解释变量后接受健康教育种类的均值。

随机截距模型的SAS程序及结果如下。

SAS程序：

proc mixed data＝mig＿c method＝reml covtest；

class c6；

model h＿edu＝n＿educ nhea＿cc

/solution ddfm＝bw notest；

random int/subject＝c6；

run；

SAS结果：(www.xing528.com)

SAS结果输出如下：

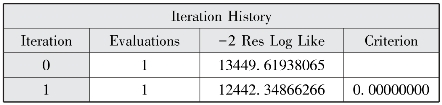
图12-6　迭代历史

图12-7　协方差参数估计

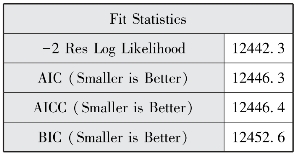
图12-8　模型拟合参数

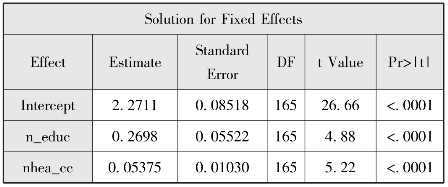
图12-9　固定效应估计

SAS结果解释：

图12-6表明模型评估经过1个迭代后就成功收敛了。图12-8报告了AIC、AICC和BIC三个信息标准值和－2LL较空模型均有所减少，说明加入控制变量和组水平变量后的模型拟合效果更好。图12-7报告了水平1随机截距方差（，p＜0.001）和水平1残差方差（，p＜0.001）估计。由于水平2解释变量仅能解释水平2变异，因此与空模型比较，水平1方差基本未减少。纳入水平2解释变量后的残差缩减比可表示为：残差缩减比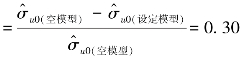。这说明纳入水平2解释变量健康教育宣传栏更新次数后，解释了大约30%的社区变异。图12-9显示健康教育宣传栏更新每增加1次，流动人口接受健康教育的种类就增加0.0538种；社区开展的健康教育种类每增加1种，流动人口接受健康教育的种类就增加0.2698种。