在多层模型出现之前，面对多层数据结构的处理方法一般是将所有变量分解或汇总到某个层次上，然后通过多元回归抑或对不同层次上的变量分别回归等传统方法进行分析。汇总的方法是将个体层面的变量汇总到更高层面，例如将个体层面的变量汇总到更高的社区水平，并在社区水平上进行回归分析。但汇总的方法不仅会导致生态学谬误（ecological fallacy），且往往会由于组内变异的流失导致结果与个体层面的分析结果有较大差异，甚至与事实背道而驰。分解的方法则将宏观层面变量纳入个体层面，例如将社区特征纳入个体模型进行回归分析，但分解法忽略了宏观层面解释变量的影响，导致宏观变量与个体变量间的高度相关性，从而使参数估计失去统计效率。对不同层次变量分别进行回归则将个体水平变量的回归系数作为宏观层面回归的结果变量，而这本质上是一种技术上的错误。通过引入方差分析、协方差分析可以部分解决上述问题，但亦存在参数较多从而大大降低解释力、使用固定效应导致研究成果推广受限、无法处理缺失数据或不平衡数据等问题（Luke，2012）。
多层模型起源于教育学，在短短二十年间它被广泛运用于各个领域，且被冠以不同称呼，如多层模型（multilevel model）、分层模型（hierarchical model）、随机系数回归模型（random-coefficient regression model）、混合效应模型（mixed effet model）、随机效应模型（random-effect model）、增长曲线模型（growth-curve model），等等。如图12-1，分层模型的总变异被明确区分为宏观变异和微观变异两种随机变异，宏观变异即为社区均值（此处为
）的差异，可以通过纳入宏观变量解释这种变异，此时变异称之为宏观残差。而微观变异为不同社区内个体的yij与各社区均值
的差异（其中i代表个体，j代表社区），可以通过纳入微观（个体层）变量解释这种变异，此时变异被称之为微观残差。此外，多层模型假定个体层面变量和宏观层面变量均可随机变化，并形成相应的复合残差结构，于是每一层都有一个嵌套模型将个体和宏观层面变量联系起来。虽然分层模型原理并不复杂，但由于非平衡数据协方差成分的复杂性，在20世纪70年代早期，依旧没有很好的方法估计这种混合残差结构。直到1977年，Dempsters等学者提出了EM算法，使协方差成分的估计成为可能，并有效地运用于分层嵌套数据的估计。此后，各类计数协方差的算法相继问世，使得分层模型也可运用于多种结局变量，如连续变量、分类变量、计数变量、次序变量，等等（Snijders T A B.，et al.，2003）。
(www.xing528.com)
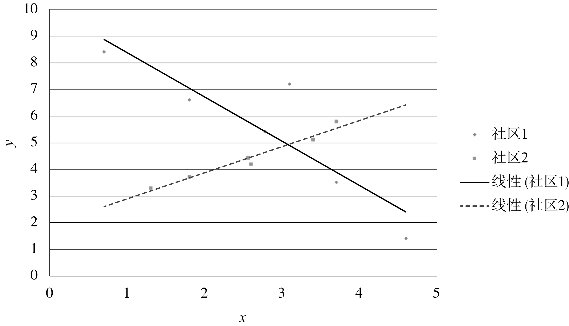
图12-1 不同社区中x对y的影响
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
