潜在类别分析概述及实现ＳＡＳ方法

LCA是以个体为中心的统计方法，采用“降维简化”技术，旨在通过少数潜类别变量来解释分类外显变量的关联，类别内的任意两个外显变量之间的关联已通过潜变量解释，进而维持外显变量局部独立性（Collins＆Lanza，2010；邱皓政，2008）。该方法通过构造分类潜变量，克服了分类变量描述的单一性，可以进一步挖掘潜在的类别。如图10-1所示，U为外显变量，可以是二分类变量、多分类变量或者两者的混合；C为潜类别变量，一般而言，潜类别数目应小于外显变量的数目；协变量X指向潜变量C的箭头表示协变量影响个体类别归属，通常采用二分类Logistic回归（两个潜类别）或无序多分类Logistic回归（潜类别数达三个及以上）分析；潜变量C指向结局变量Y的箭头表示潜在类别可以预测结局变量，根据结局变量的类型（连续型变量、分类变量、计数变量等）选择不同的统计方法。通过LCA可以识别相对同质的亚组，进而分析其影响因素和对远端结局事件的影响（王孟成、毕向阳，2018）。当潜在类别分析不带有任何协变量和结局变量时，称之为无条件的潜在类别分析（unconditional latent class analysis），即图10-1中不含有变量X和Y。

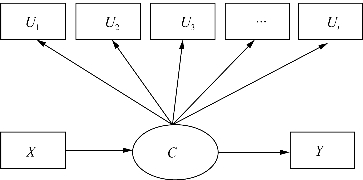
图10-1　潜在类别分析(www.xing528.com)

基于研究目的的不同，LCA可以分为探索性和验证性LCA。探索性LCA事先并不知道潜类别的数目，以未设限的方式进行参数估计，完全由观察数据来决定模型。而验证性LCA在进行分析之前提出一个先验的假设模型，通过增加参数限制来检验特定的假设，与观察数据进行对比，来决定是否支持假设模型。参数限制的类型主要包括等值限定、定值限定和不等值限定，一般而言，模型限定主要针对条件概率。例如，条件概率等值的多组分析，通过等值限定使得在不同组的个体在相同的潜类别内有相同的条件概率，即为等值设定。等值限定使得模型更加简洁，应用价值较高。定值限定是将模型中的参数给予特定的数值（通常是0或1），而不是让参数自由估计，实际应用中很难给定具体的概率值，因此使用较少。目前已经有多种软件可以进行LCA，如：Mplus、SAS、Stata、R、LatentGOLD等。本节主要介绍了LCA的一些基本概念、模型拟合评价指标、模型估计步骤、无条件LCA的SAS实现等内容。