多元统计分析实例与SAS工具演示

本节将数据集命名为exe9来演示CFA，原始数据取自国家卫生健康委员会设计并组织实施的2014年全国流动人口卫生计生动态监测调查C卷部分。该调查旨在了解国内流动人口的社会融合与心理健康状况。调查范围覆盖北京市朝阳区、福建省厦门市、浙江省嘉兴市、四川省成都市等8个城市（区），采用分层、多阶段、与规模成比例的PPS方法进行抽样，每个城市（区）流动人口样本量为2000人，8个城市（区）共计16000人。经过缺失值处理后，本次分析有效样本量为15997。

本章模型构建中所涉及的变量如下：

n1—n6：连续变量，为消极情绪体验量表的测量指标；

l1—l5：连续变量，为生活满意度量表的测量指标；

p1—p5：连续变量，为身体健康量表的测量指标。

本节，我们使用以上变量来介绍CFA的SAS实例操作。基于已有文献理论，我们使用变量n1—n6作为流动人口的消极情绪体验（f1）的观测指标，变量l1—l5作为生活满意度（f2）的观测指标，p1—p5作为身体健康（f3）的观测指标。参考已有研究（Hu＆Bentler，1999；温忠麟等，2004），本节对模型进行了如下设定：模型中共有16个测量变量（n1—n6，l1—l5，p1—p5）和3个潜在变量（f1—f3），每个潜在变量分别由对应的测量变量来测量（见图9-2），并假定测量变量的误差项之间不相关，不同潜在变量的指示变量之间不相关，各潜在变量之间也不相关，因子的方差设定为1。首先将电脑桌面上的sav数据文件命名为“exe9”，随后导入数据，运行具体的CFA程序。上述步骤的SAS语句如下所示。

图9-2　设定的模型

SAS程序：

proc calis data＝exe9 mod；

lineqs

n1＝f1＋e1，n2＝a1 f1＋e2，n3＝a2 f1＋e3，n4＝a3 f1＋e4，n5＝a4 f1＋e5，n6＝a5 f1＋e6，

l1＝f2＋e7，l2＝a6 f2＋e8，l3＝a7 f2＋e9，l4＝a8 f2＋e10，l5＝a9 f2＋e11，

p1＝f3＋e12，p2＝a10 f3＋e13，p3＝a11 f3＋e14，p4＝a12 f3＋e15，p5＝a13 f3＋e16；

std

e1－e16＝var1－var16；

run；

SAS程序解释：

proc calis为进行CFA的过程步，可用于多变量线性回归分析、路径分析、CFA和SEM。mod输出固定参数的修正指标的预期估计，默认使用ML估计法。lineqs语句设定方程等式，CFA中等式的表达方法：观测变量＝因子载荷×潜在变量＋残差项。std语句指出矩阵要估计的方差，并给方差命名。

SAS结果：

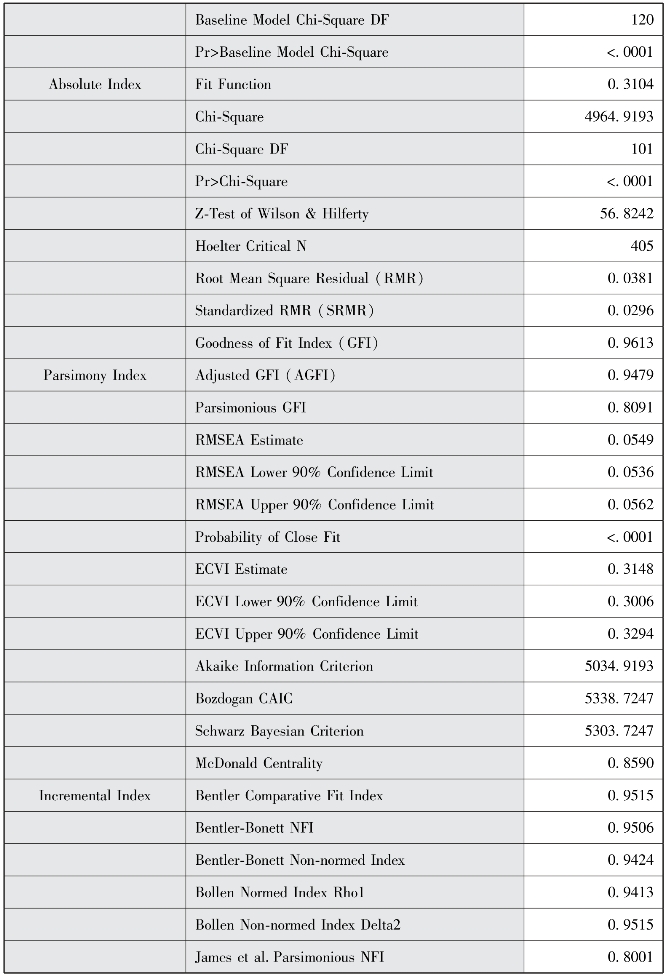
图9-3　模型拟合结果

图9-4　误差方差和协方差的10个最大LM统计量的秩次

SAS结果解释：

图9-3显示CFA的拟合结果如下：SRMR＝0.0296，RMSEA＝0.0549，GFI＝0.9613，CFI＝0.9515，NFI＝0.9506，模型拟合良好。图9-4显示了最大的10个MI值，我们可以根据MI指数进行模型的修正，从而实现更好的模型拟合，SAS语句如下：

SAS程序：

proc calis data＝exe9 mod；

lineqs(www.xing528.com)

n1＝f1＋e1，n2＝a1 f1＋e2，n3＝a2 f1＋e3，n4＝a3 f1＋e4，n5＝a4 f1＋e5，n6＝a5 f1＋e6，

l1＝f2＋e7，l2＝a6 f2＋e8，l3＝a7 f2＋e9，l4＝a8 f2＋e10，l5＝a9 f2＋e11，

p1＝f3＋e12，p2＝a10 f3＋e13，p3＝a11 f3＋e14，p4＝a12 f3＋e15，p5＝a13 f3＋e16；

std

e1－e16＝var1－var16；

cov

e13 e15＝cove13e15；

run；

SAS程序解释：

cov为协方差设定的语句，根据拟合结果及MI值进行相关设定。依据模型的简约性法则，一般选取最大的MI值进行协方差设定，拟合达标后便不再添加相关。需要注意的是，只能将测量变量间的残差纳入设定协方差。

SAS结果：

图9-5　模型拟合结果

SAS结果解释：

图9-5显示CFA的拟合结果如下：SRMR＝0.0303，RMSEA＝0.0493，GFI＝0.9691，CFI＝0.9612，NFI＝0.9602，两次模型拟合结果对比情况如表9-2所示。由表9-2我们可以发现，大部分拟合指标都得到了改善。当然，这里我们添加协方差相关是假设原模型拟合结果较差进行的操作演示。实际应用中，根据模型简约性原则，如果初始模型拟合较好，便不再需要进行相关设定。

表9-2　模型修正前后拟合结果对比

我们继续来看模型估计的结果。图9-6展示了测量模型的标准化系数结果、残差和协方差相关系数。

图9-6　线性方程组的标准化结果

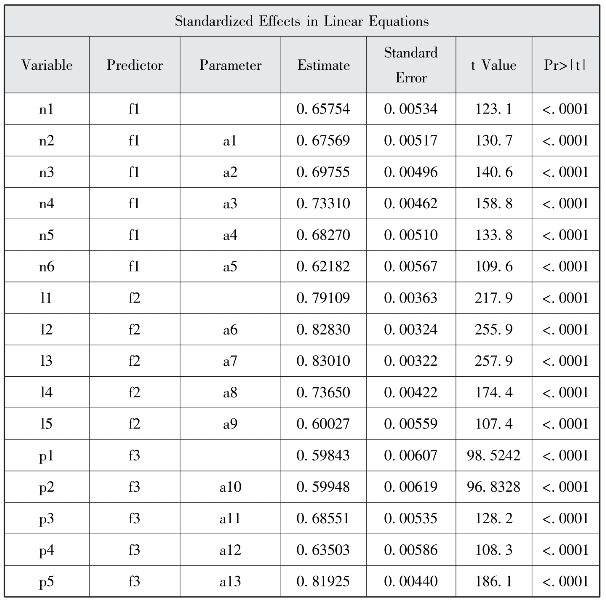
图9-7　线性方程组的标准化结果

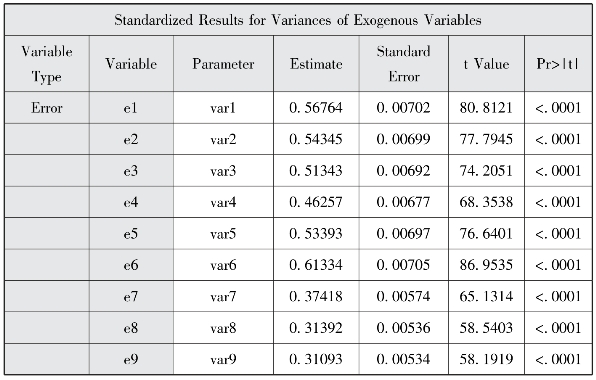
图9-8　外生变量方差的标准化结果

图9-9　外生变量间协方差的标准化结果

SAS结果解释：

根据图9-7到图9-9，我们可以得到测量模型的标准化路径系数、残差及残差协方差，并得到相应的测量方程。各系数均在统计意义上显著（p＜0.0001）。测量方程如下：n1＝0.6575×f1＋0.5676；n2＝0.6757×f1＋0.5435；……；p5＝0.8193×f3＋0.3288。e13与e15之间的协方差为0.1817。