Bayes判别法实例分析及SAS实现

7.2.3.1　Bayes判别法简介

Bayes准则的判别方法，该方法根据概率的大小进行判别，要求各类近似服从多元正态分布。多类判别时多采用此方法。采取Bayes判别准则，使得每一类中的每个样本都以最大的概率进入这一类中。

Bayes判别的步骤如下：和Fisher判别的步骤一样，首先我们需要建立一个Bayes判别函数。若已知有g类记为Yk（k＝1，2，…，g），m个判别指标Xj（j＝1，2，…，m），假定某判别对象各指标Xj的状态分别取为Sj（i＝1，2，…，m），则该对象属于第k类的后验概率为下式中所求得概率，其中，式中P（Yk）为第k类出现的概率，或称为事前概率。

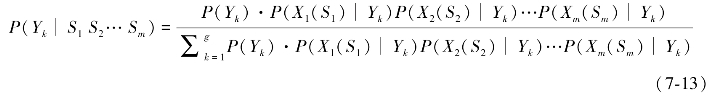
第二步，建立Bayes判别准则，将判别对象判为最大的那一类。

第三步，估计各项指标对判别函数的作用大小。我们可以用以下三种方法进行估计。

（1）一元方差分析：它检验每一个指标变量对判别函数的判别能力是否有显著性意义。

（2）多元方差分析：它检验所有指标变量联合对判别函数的判别能力是否有显著性意义。

（3）值得注意的是，若判别函数中特异性强的指标越多，则判别函数的判别功能也越强。

7.2.3.2　实例分析与SAS实现

判别分析可以对聚类分析中样品聚类结果中分成的类别进行判断其分类是否合理（Wang et al，2007；Ma et al，2006），我们使用样品聚类中的例子来判断将15个地区分成四类是否合理，首先要说明的是，判别分析中允许每一类的样本量不必相同，我们选用第一类的3个样本、其余三类挑选4个样本作为此次的样本量，共计15个，我们对数据调整如表7-5所示。

表7-5　2018年度我国15个地区医疗卫生服务相关统计数据

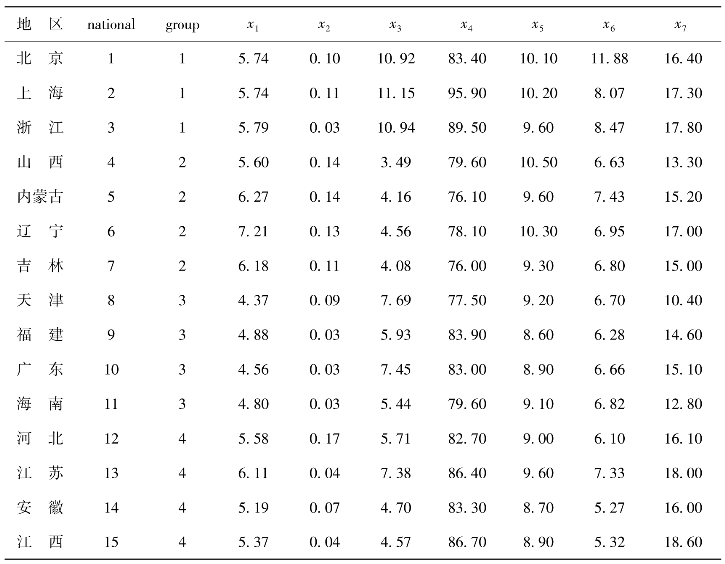
需要说明的是，SAS软件中的判别分析过程是以Bayes判别分析法为理论基础进行分析，本节的数据集命名为exe7＿2。

SAS程序：

data　a2；

input national group x1－x7＠＠；

cards；

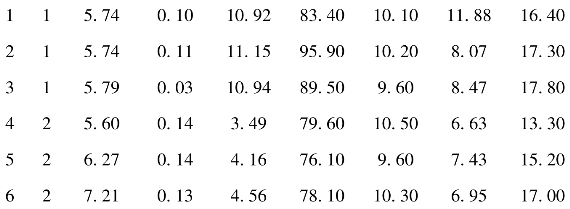
续表

proc discrim data＝a2；

outstat＝out　anova manova pool＝test listerr posterr；

class group；

var x1－x7；

priors prop；

run；

SAS程序解释：(www.xing528.com)

proc discrim表示使用判别分析方法。outstat表示输出结果的SAS数据集名，用来保存判别分析输出的结果（均值、标准差、判别函数的系数等）。anova表示每一个指标变量的一元方差分析结果，用于检验每一个指标变量在每一类上的均值是否都相等，如果拒绝无效假设，则说明该指标变量对判别函数的判别能力有显著意义。manova表示输出所有指标变量的多元方差分析结果，用于检验所有指标在每一类上的均值是否都相等，如果拒绝无效假设，则说明指标变量的联合作用对判别函数的判别能力有显著性意义。pool表示用来选择方差协方差矩阵的形式，当pool＝yes时表示系统选择归并的方差协方差矩阵，这时输出的判别函数是一次线性函数；当pool＝no时选择类内的方差协方差矩阵，这时输出的判别函数是二次线性函数；当pool＝test时不仅可以用来检验类间方差的一致性，还可以根据检验结果自动确定在判别函数中使用哪一种方差协方差矩阵，一般选择这个是最简单、最便捷的方法。listerr或list输出样本的回代结果，包括每一个样本的事后概率以及根据Bayes判别准则重新分类的准确率和错误率。posterr表示用所建立的判别函数来判别，观测归属于函数值大的类别（李君艺、梁智城，2011）。priors prop表示的是事前概率等于样本的估计值。

SAS结果：

SAS部分结果输出如下：

图7-18　分类水平信息

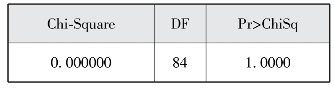
图7-19　分类内协方差矩阵的齐性检验

Since the Chi-Square value is not significant at the 0.1 level，a pooled covariance matrix will be used in the discriminant function.

Reference:Morrison，D.F.(1976)Multivariate Statistical Methods p252.

图7-20　一元检验统计量

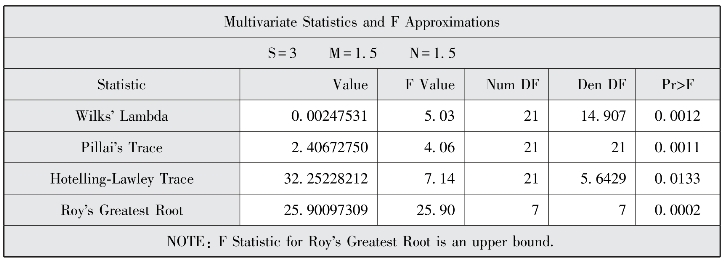
图7-21　多元检验统计量

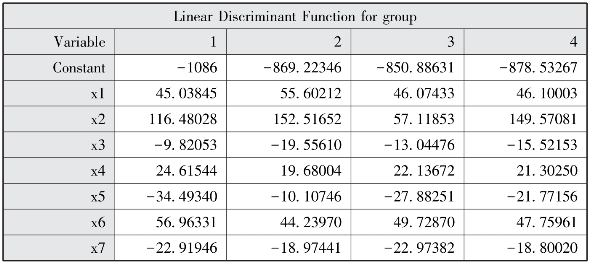
图7-22　以下对象的线性判别函数：组别

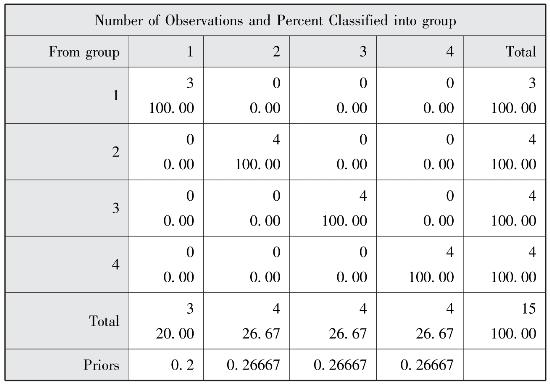
图7-23　分入“组别”的观测数和百分比

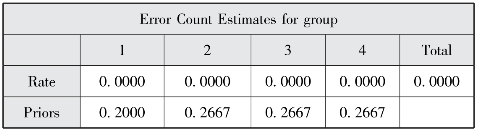
图7-24　“组别”的出错数估计

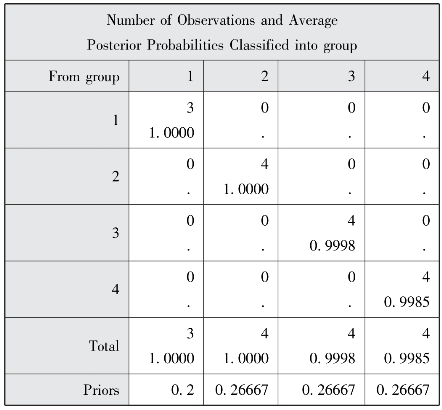
图7-25　分入“组别”的观测数和平均后验概率

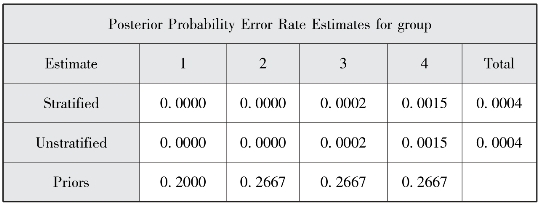
图7-26　“组别”的后验概率出错率估计

SAS结果解释：

上面的结果中，图7-18显示的是事前概率，在这里，事前概率和样本估计值是相等的。图7-19显示的是类内方差协方差的一致性检验结果，检验结果p＝1.000，表明类内方差协方差一致，因此，应使用归并的方差协方差进行判别函数的参数估计。若此处的p＜0.10，则表明类内方差协方差不一致，应使用分类内的方差协方差进行判别函数的参数估计。图7-20是单变量方差分析，结果显示变量x1（p＝0.0014）、x3（p＜0.0001）、x4（p＝0.0039）、x5（p＝0.0079）、x6（p＝0.0070）、x7（p＝0.0141），这6个指标对判别函数有显著意义。图7-21表示的是多变量方差分析的结果，7个指标的联合作用有显著性意义（p＝0.0012）。图7-22是线性判别函数估计值，这一步可以得到相应的判别函数表达式如下：

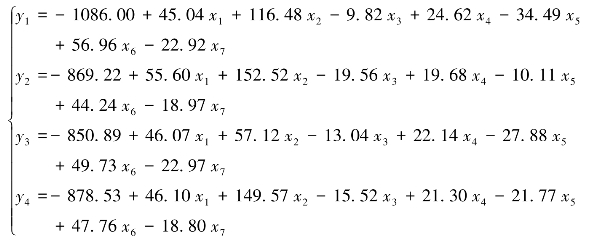
图7-23和图7-24是错判样本的事后概率，本结果显示，没有样本被错误判别。图7-25和图7-26是回代结果和错判率估计，从回代结果来看，四类的错判率以及总错判率估计是0.0000。第一、二类的事后概率错误率估计是0.0000，第三类事后概率错误率估计是0.02%，第四类事后概率错误率估计是0.15%，总事后概率错误率估计是0.04%。总的来看，这个判别函数的错误率较低，可以使用。我们用聚类分析例子中对样本所分的类来进行判别分析，也借助判别分析进一步验证了聚类结果的可靠性，完成了对新样本的判别归类研究。