7.1.3.1 K-均值聚类法简介
系统聚类特别适用于小样本情形,需要嵌套聚类并得到有意义的层次结构。对样品聚类,如果样本量很大,那么使用系统聚类法的计算量会非常大,做出的树状图也很复杂,不便于进行分析,此时便可以采用K-均值聚类(K-means clustering),其又称快速聚类、动态聚类(陈峰,2001;孙振球等,2014),这种方法首先会给出一个初始的聚类方法,再按照某种最优法则进行一步步调整,直到得出最优的聚类方法,则停止聚类过程。K-均值聚类中的K表示聚类算法中的分类数,K-means即是用均值算法把样本分成K个类的聚类方法。K-均值聚类分析事先要给定类别的个数K,进行初始分类。然后按照某种准则对这一初始分类进行逐步修改,直到分类的结果比较合理(稳定)为止。该方法计算速度较快,所以称为快速聚类法。这个算法是很经典的在距离基础上的非层次聚类算法,基于最小化误差函数将数据划分为预定的类数K,采用距离来当作相似性的评价指标,也就是认为两个对象的距离越近,其相似度就越高(王彤,2008)。方法步骤如下:
(1)取得K个初始质心(凝聚点):从数据中随机抽取K个点作为初始聚类的中心,以此来代表各个类。
(2)把每个点划分到相应的类内:根据欧氏距离最小原则,将每个数据点归类到离它最近的那个中心点所代表的类中。
(3)重新计算质心:根据均值等方法,重新计算K个聚类的质心。
(4)循环:用计算出的质心重新进行聚类,与前一次计算得到的K个聚类质心比较,如果聚类中心发生变化,转过程(2)重复第二步和第三步,否则转过程(5)。
(5)聚类完成:每一类均稳定,即凝聚点不再发生变化时,聚类过程结束。7.1.3.2 实例分析与SAS实现
用K-均值聚类分析以上例子,但需要注意的是K-均值聚类适用于大样本,对于仅含31个样本的数据是不需要用K-均值聚类中proc fastclus过程步的,但此处为了给大家与SAS程序中的proc cluster过程步进行比较,故例子选用和样品聚类分析的例子一样,注意这里仅用来举例说明方法。
SAS程序:
proc standard data=a1 mean=0 std=1 out=b1;
var x1-x7;
run;
proc fastclus data=b1 maxc=3 distance radius=1 maxiter=10;
var x1-x7;
run;
proc fastclus data=b1 maxc=4 distance radius=1 maxiter=10;
var x1-x7;
run;
proc fastclus data=b1 maxc=5 distance radius=1 maxiter=10;
var x1-x7;
run;(https://www.xing528.com)
SAS程序解释:
我们需要用proc standard过程步将原始数据标准化,proc fastclus表示我们使用K-均值聚类法对数据进行分析,maxc表示的是我们限制SAS软件分析时定的最大分类数,这是因为聚类的结果可能依赖于初始聚类中心的随机选择,可能使得结果严重偏离全局最优分类,因此在实践中,为了得到较好的结果,通常选择不同初始聚类中心,多次运行K-Means算法。上面我们已经知道31个样本分为4类比较好,故我们的最大分类数取3、4、5类。
SAS结果:
SAS部分结果输出如下:
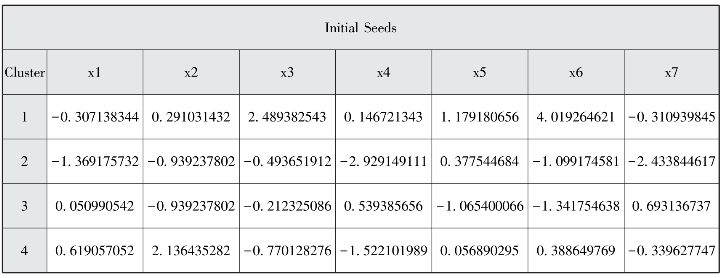
图7-12 初始种子
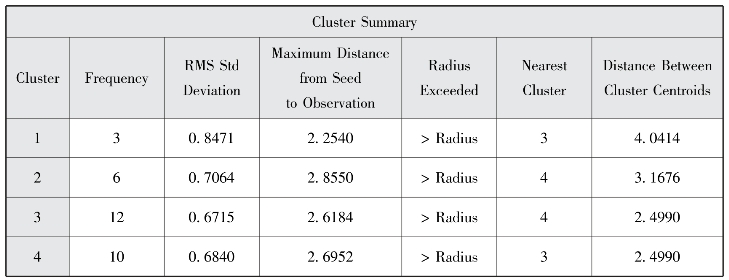
图7-13 聚类汇总
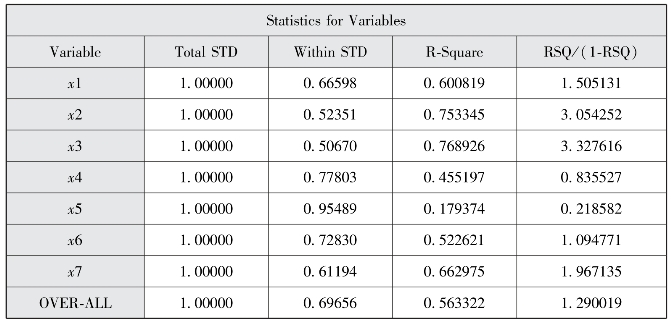
图7-14 变量的统计量
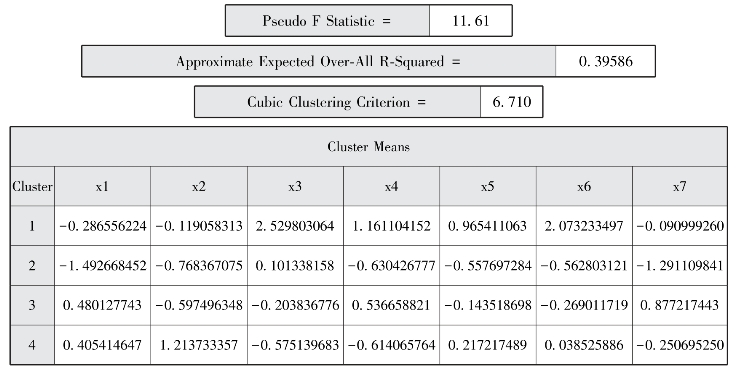
图7-15 聚类均值

图7-16 聚类标准差
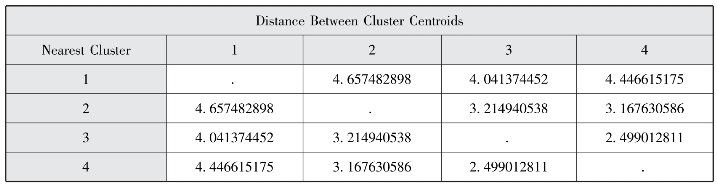
图7-17 聚类质心之间的距离
SAS结果解释:
首先要说明的是,对于K-均值聚类法来说是没有聚类树状图的,想象一下假如样本量有200,那么我们的聚类树状图是画不出来的,此方法只能简单地知道把样本分为了几类,根据指标对样本分成的类别进行解释。上面的结果显示了当聚类数为4时的详细结果,当我们设定最大聚类数为3或5时,结果解释与4相似。我们根据SAS输出的统计量(见表7-4),相比较可以得知当分类数为4时,分类效果较好,分析聚类数为4时,图7-13和图7-15显示,第一类包含3个样本,类别均值中x3、x4、x5、x6的均值最大,说明这组分类中的样本,其卫生医疗资源利用率较高。第二类包含6个样本,这一类其指标的均值都偏小,说明这组分类中的样本,其卫生医疗资源利用率偏差。第三类包含12个样本,类别均值中x1、x7的均值最大。第四类包含10个样本,类别均值中x2的均值最大。由此我们得知,proc fastclus过程步和proc cluster过程步得出的结果对样本的归类还是有一定的差异的,但需要知道的是前者可以得到聚类后的类内指标均值,从而找出类间的区别或每一类的特性。
表7-4 不同分类数的聚类统计量

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




