多元统计分析与SAS实现中的实例分析

7.1.2.1　系统聚类法简介

系统聚类法（hierarchical clustering），又称层次聚类，是先把n个被聚对象（样本或观察指标）看成n个类，然后按聚类指标将相近（相似）的两类归并为一类，这样逐步归并，类数逐次减1直至将n个被聚对象并为一类为止。系统聚类不指定具体的类别个数，而只关注类之间的远近，最终会形成一个树形图或谱系图（dendrogram）。谱系图中聚类结果呈嵌套关系或者层次关系，层次聚类由此得名。

1.类间距离

对被聚对象进行了第一次归类后，某一类含有多个被聚对象，就需要定义新类与其余类间的距离。由于类的形状较多，所以类与类之间的距离也有较多的计算方式。类与类之间距离的定义不同，即指定类的邻近准则不同，得到计算类之间距离的公式也不同，最终计算出的距离大小也就不同。

用Gp，Gq分别表示两类，各自含有np，nq个样本或变量。设某一步把类Gp和Gq归并为Gr，Gr与其他类Gk的八种距离计算公式，如公式（7-1），其中，Dkr为类Gk和类Gj之间的距离，ap、aq、β和γ针对不同的类间距离计算方法的取值如表7-1所示。

表7-1　类间距离统一公式参数表

续表

注意：以上八种方法的选取没有一个合适的标准，其中，可变法由中间距离法变形而来（β＜1，通常情况下取－1～0的数），类平均法和离差平方和法（Ward法）最常用，重心法和Ward法只能用于样品聚类且必须用欧氏距离。非参数概率密度估计法、最大似然法、Mcquitty的相似分析法、两阶段密度法不能与以上八种方法一起比较，故没有列出。

2.分类数的确定

聚类分析的目的是对研究对象进行分类，因此分类数的确定是聚类分析的重要问题之一。由于类的结构难以统一定义，加上聚类分析本质是探索性分析，下面仅提供一些辅助确定类别个数的方法作为实际参考。

（1）观测散点图：当样本只有两个变量或者三个变量时，可参考观测数据的散点图来定类别个数。

（2）根据事先给定的类间距的阈值：通过观察系统聚类的谱系图，征询专家的看法，来定一个切合的阈值d*，要求类与类之间的距离大于d*。

（3）使用统计量：如R2统计量、偏R2统计量、伪F统计量、伪t2统计量和立方聚类准则。

R2统计量，如公式（7-2），其中，∑Di为在谱系的第G层对G个类的类内离差平方和，TSS为所有观察的总离差平方和。通常来说，R2统计量用来评价每次归并成G个类时的聚类效果。当R2统计量越大，越靠近1，表明类内离差平方和∑Di在总离差平方和TSS中所占的比重越小，说明这G个类越能分得开，故聚类效果越好。R2的值总是在0和1之间，当n个样本各自为一类时，R2＝1；当n个样本最后归并成一类时，R2＝0。因为R2的值总是随着分类个数的减少而变小，比较理想的聚类结果是R2尽可能大而类的个数尽可能少。

半偏R2统计量，如公式（7-3），归并类Gp和类Gq为类Gm时，可以用半偏（semipartial）R2统计量评价本次归并的效果。其中，Dw（p，q）表明归并类Gp和类Gq为新类Gm后，类内离差平方和的增量。半偏R2值是上一步归并后R2值与本次归并后R2值的差。它的值越大，表明上一步归并后停止归并的效果更好。

伪F统计量，如公式（7-4），其中，G为聚类的个数，n为观察总数。伪F值越大表明分为G个类的效果越好，所以应该取伪F统计量较大而类数较小的聚类水平。

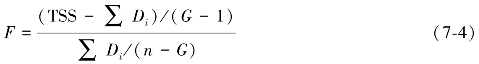
伪t2统计量，如公式（7-5），该统计量用以评价归并类Gp和类Gq的效果，表示归并类Gp和类Gq为类Gm后离差平方和的增加量（Dm－Dp－Dq）对于原本Gp和Gq两类的类内离差平方和的大小。它的值越大，表明刚刚归并的两个类Gp和Gq是很分开的，也就是上一步聚类的效果好。

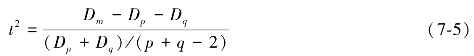
立方聚类准则（cubic clustering criterion，CCC）：在均匀的原假设下判断聚类分成几类合适的一种准则，大的CCC值表示好的聚类，峰值表示建议分类数。

（4）Demirmen在1972年曾提出根据树形图进行分类的准则：任何类都得在邻近各个类别中是突出的，即各类重心间距离必须十分大；定好的类中，各类所包含的元素都不要过多；分类的数目必须符合实用目的；若采取几种不同的聚类方法，则在各自的聚类系谱图中应发现同一类。

那么，系统聚类分析法的步骤是什么样子呢？下面我们来介绍。以n个样本的聚类分析作为分析例子，其步骤如下：（1）我们定义用样本或指标的个数为维度空间里的一种距离；计算n个样本二者之间的距离。（2）将每个样本归为一类，根据计算出的样本间距离归并距离最近的两类为一个新的类别。（3）再计算这个新类别与其他各类的距离，同样再由计算出的距离归并距离最近的两类为一个新的类别。（4）循环以上步骤直到类别个数为1的时候停止。（5）画出各阶段的聚类系谱图，最终决定类别的个数（汪海波等，2013）。

7.1.2.2　实例分析与SAS实现

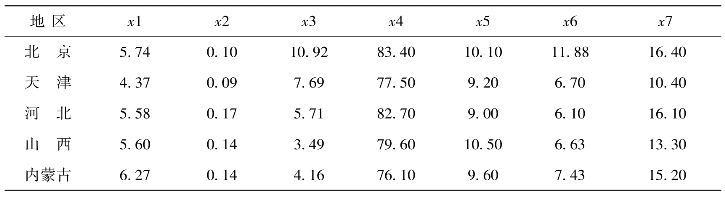
系统聚类还可以分为Q型聚类和R型聚类，Q型聚类用于样品聚类，是对样本进行分类处理，目的是找出样本间的共性以指导实际工作；R型聚类用于指标聚类，是对指标进行分类处理，目的是降维后便于在每类中选择有代表性的变量，或者利用少数几个重要变量进一步进行其他分析。表7-2为我国2018年度31个地区医疗卫生服务相关统计数据。

表7-2　2018年我国31个地区医疗卫生服务相关统计数据

续表

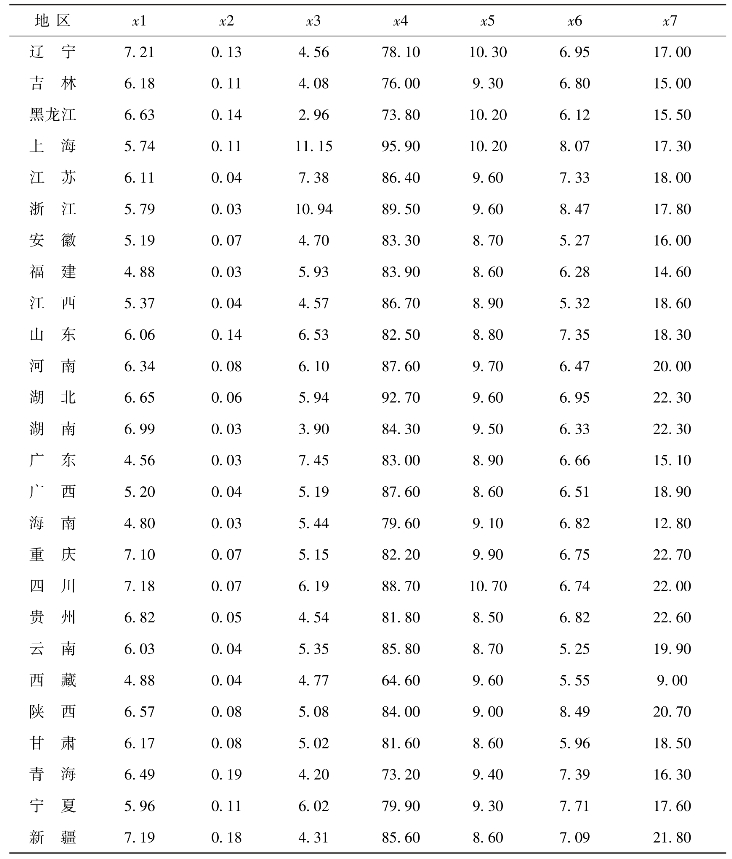
注：原始数据来源于《中国统计年鉴》（2018年）。其中，x1表示每千人口拥有医疗卫生机构床位数（张/千人）；x2表示急诊病死率（%）；x3表示居民平均就诊次数（次）；x4表示病床使用率（%）；x5表示出院者平均住院日（天）；x6表示每千人口拥有卫生技术人员数（人/千人）；x7表示居民年住院率（%）。对31个地区进行聚类分析，我们称此类为样品聚类，即Q型聚类；对x1—x7这7个变量进行聚类，称为指标聚类，即R型聚类。

我们使用表7-2中的数据进行操作演示。首先我们将地区进行编号：“北京—新疆”依次编为“1—31”从而对汉字进行替换，并将地区改命名为“national”，本节将其数据命名为exe7＿1。先对31个地区进行聚类分析（样品聚类，即Q型聚类）。

SAS程序：

proc import datafile＝"C:＼Users＼Administrator＼Desktop＼exe7＿1"out＝a1 dbms＝xlsx；

run；

proc cluster data＝a1 method＝ward std pseudo ccc；

var x1－x7；

id national；

run；

SAS程序解释：

proc cluster表示我们使用系统聚类中的样品聚类法对数据进行分析，method＝ward表示我们的类间距离选择离差平方和法（ward），pseudo表示计算F和伪t2统计量，ccc表示计算R2、半偏R2和CCC统计量。method有多种选项，如average，centroid，complete，density，eml，flexible，mcquitty，median，single，twostage，ward（汪海波等，2013），对应的方法分别为：类平均法；重心法；最长距离法；非参数概率密度估计法；最大似然法；可变类平均法；mcquitty的相似分析法；中间距离法；最短距离法；两阶段密度法；离差平方和法，其中除eml外前一项均为后一项的缩写，输入程序时，两者皆可。

SAS结果：(www.xing528.com)

SAS部分结果输出如下：

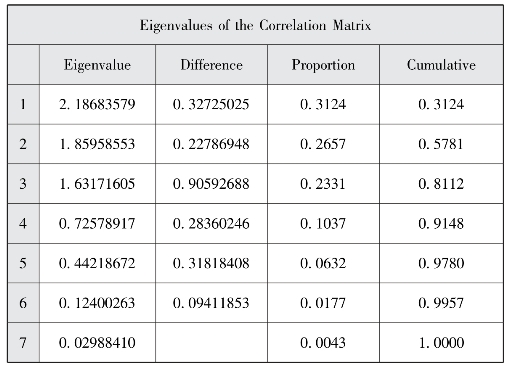
图7-1　相关矩阵的特征值

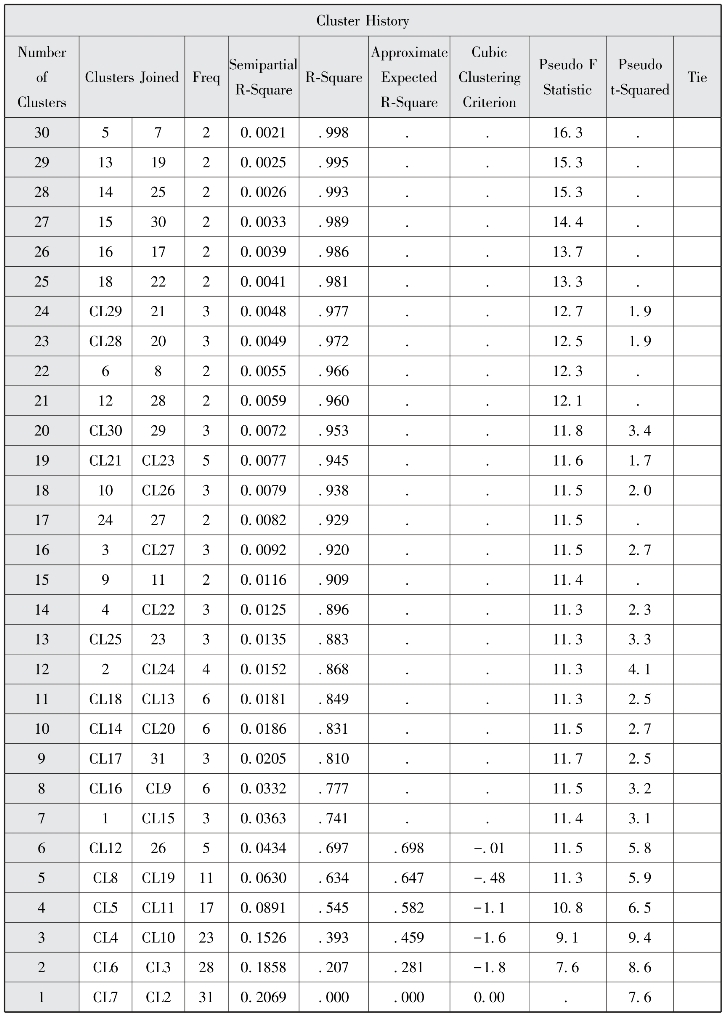
图7-2　聚类历史

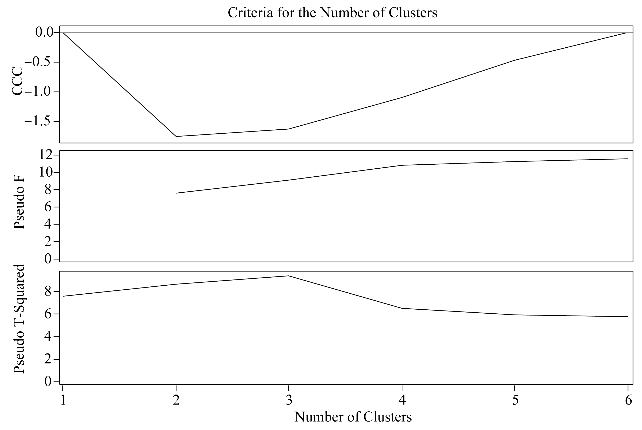
图7-3　聚类数准则

图7-4　聚类分析

SAS结果解释：

为了消除原始数据量纲的影响，将原始数据进行标准化处理。上面的结果中，图7-1显示的是基本信息，这是用离差平方和法进行样品聚类分析的结果。图7-2显示的是聚类样本的过程及分类指标。图7-3显示的是程序CCC的输出统计图，它与图7-2结合来判断聚成几类更为合理，表7-3列出了判断聚类数目的五个统计量（详细知识请参考前面介绍的五个统计量来判断最佳聚类数目）。图7-4显示的是聚类树状图，它显示出了各种可能的聚类结果，图的横轴是聚类的个数，纵轴是指标变量名。

结合聚类谱系图以及软件输出的分类数统计量可以看出聚为4类效果较好。最终聚类结果为：第一类：内蒙古，吉林，山西，青海，辽宁，黑龙江。第二类：安徽，江西，广西，云南，山东，宁夏，河北，甘肃，湖南，重庆，陕西，新疆，贵州，江苏，河南，湖北，四川。第三类：天津，福建，广东，海南，西藏。第四类：上海，浙江，北京。结果表明我国31个省市总体医疗卫生资源分配不均衡。北京、上海以及浙江3个地区的卫生医疗资源利用率较高，卫生服务条件在全国居于领先（Sun et al.，2018）；中西部几个经济比较落后的省份卫生服务条件以及卫生资源不理想，其他地区医疗资源及服务条件尚可。

表7-3　不同分类数的聚类统计量

接下来我们对x1—x7这7个变量进行聚类分析，即指标聚类（R型聚类）。

SAS程序：

proc varclus data＝a1；

var x1－x7；

run；

其中，proc varclus表示我们使用系统聚类中的指标聚类法对数据进行分析。

SAS结果：

SAS部分结果输出如下：

图7-5　1个聚类的聚类汇总

Total variation explained＝2.186836 Proportion＝0.3124

Cluster 1 will be split because it has the largest second eigenvalue，1.859586，which is greater than the MAXEIGEN＝1 value.

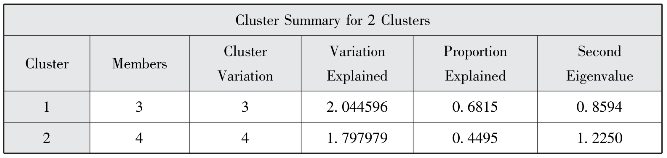
图7-6　2个聚类的聚类汇总

Total variation explained＝3.842576 Proportion＝0.5489

图7-7　2个聚类的统计量

Cluster 2 will be split because it has the largest second eigenvalue，1.224988，which is greater than the MAXEIGEN＝1 value.

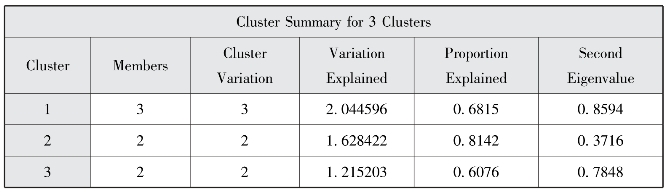
图7-8　3个聚类的聚类汇总

Total variation explained＝4.888221 Proportion＝0.6983

图7-9　3个聚类的统计量

No cluster meets the criterion for splitting.

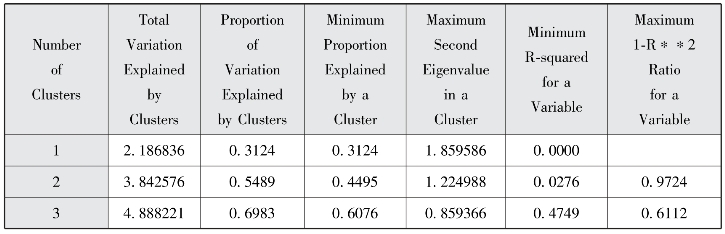
图7-10　聚类分析汇总

图7-11　聚类树状图

SAS结果解释：

上面的结果中，图7-5显示7个指标聚为一类时的概括总结，结果显示当7个指标聚为一类时，7个指标变量总体变异的31.24%被类所解释。图7-6显示的是，7个指标聚为2类的结果，其中我们主要看的是第一个表格，7个指标总体变异的54.89%被类所解释，其中，第一个类中指标变量总体变异的68.15%被类所解释，第二个类中指标变量总体变异的44.95%被类所解释，一般地，SAS软件做聚类分析时，当两类指标变量总体变异被该类所解释的比例大于75%时，停止聚类，此处小于75%，所以继续进行聚类。图7-8显示聚为三类时，我们发现7个指标总体变异的69.83%被类所解释，其中，第一个类中指标变量总体变异的68.15%被类所解释，第二个类中指标变量总体变异的81.42%被类所解释，第三个类中指标变量总体变异的60.76%被类所解释。此时我们发现7个指标总体变异的69.83%被类所解释，虽未达到75%以上，但SAS系统停止了继续分为四类的步骤，故这显示聚为3类较恰当。图7-10显示的是聚类分析总表，列出了分成1、2、3类聚类结果的统计量。图7-11显示的是聚类树状图，它显示出各种可能的聚类方法，图的横轴是聚类的个数，纵轴是指标变量名。从聚类谱系图并结合第三部分可以看出聚为3类效果较好。最终聚类结果为：第一类：x1每千人口拥有的医疗卫生机构床位数，x4病床使用率，x7居民年住院率。第二类：x2急诊病死率，x5出院者平均住院日。第三类：x3居民平均就诊次数，x6每千人口拥有的卫生技术人员数。