本节将使用2017年湖北省流动人口动态监测调查分析流动人口流动过的城市数量(除本地外)的影响因素,样本量为5000。因变量是“除本地外流动过的城市数量”。自变量包括了两种类型的指标:一是性别、年龄、受教育程度、婚姻状况、民族等个体指标;二是包括流动范围和流动时间的流动特征指标。将其数据命名为数据集exe5来演示Poisson回归,其变量赋值具体如下。
因变量:
y:除本地外流动过的城市数量(计数资料)
自变量:
gender:性别(1=男性,2=女性)
age:年龄(连续变量)
education:受教育程度(1=小学及以下;2=初中;3=高中;4=大专及以上)
marry:婚姻状况(1=在婚;2=非在婚)
ethnic:民族(1=少数民族2=汉族)
range:流动范围(1=跨省流动,2=省内跨市,3=市内跨县)
time:流动时间(连续变量)
SAS程序:
proc genmod data=exe 5;
class gender education marry ethnic range/param=ref ref=first;
model y=gender age education marry ethnic range time/link=log dist=nb noscale;
run;
proc genmoddata=exe 5;
class education marry ethnic range/param=ref ref=first;
model y=gender age education marry ethnic range time/link=log dist=poisson type1 type3 scale=deviance;
run;
SAS程序解释:
class语句的作用是在分析的过程中定义分类变量,这里表示性别、受教育程度、婚姻状况、民族、流动范围是分类变量。
proc genmod过程可以实现Poisson回归模型的参数估计和拟合优检验。(https://www.xing528.com)
第一个proc genmod过程是用来检验数据是否存在过离散现象。对是否存在过离散现象进行检验的方法有z检验和Lagrange乘子检验,proc genmod过程可以进行Lagrange乘子检验。在该过程中,通过dist=nb拟合负二项回归模型,并使用选项noscale来输出Lagrange乘子检验的结果。选项link=log指定链接函数为对数函数。
第二个proc genmod过程中,model语句中选项dist=poisson指定资料中因变量(误差项)的分布为Poisson分布,type1选项要求给出第一型分析似然比统计量,即要求程序给出模型从截距项到指定的所有变量逐个引入时的偏差统计量,type3选项要求给出第三型分析似然比统计量,即要求给出每个因素和层别效应统计量。“scale=deviance”选项是对过离散参数进行估计。
SAS结果:
SAS输出结果如下:
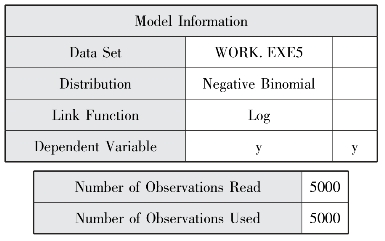
图5-1 模型信息
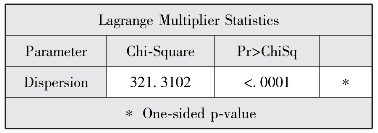
图5-2 Lagrange乘子统计量结果
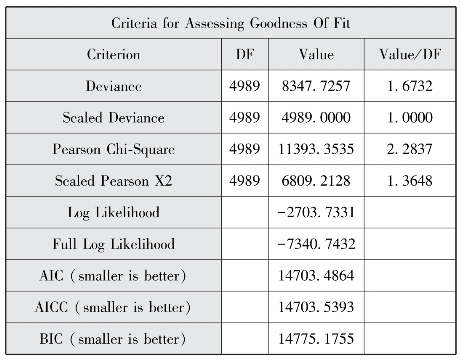
图5-3 模型拟合优度检验结果
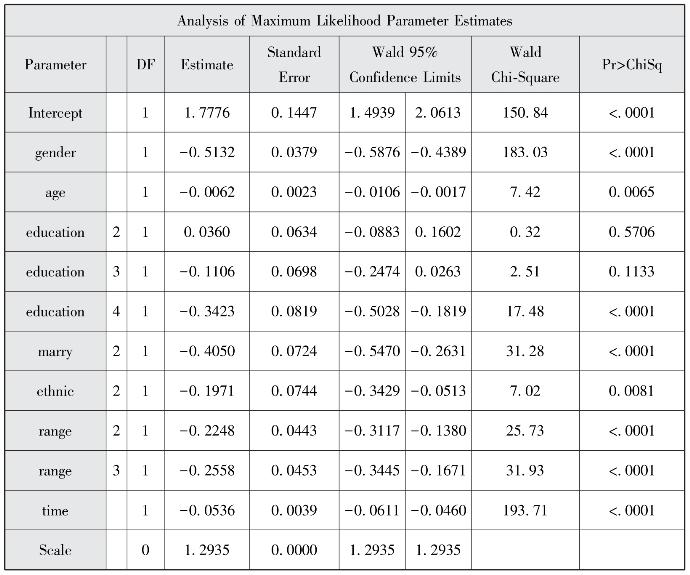
图5-4 参数估计结果
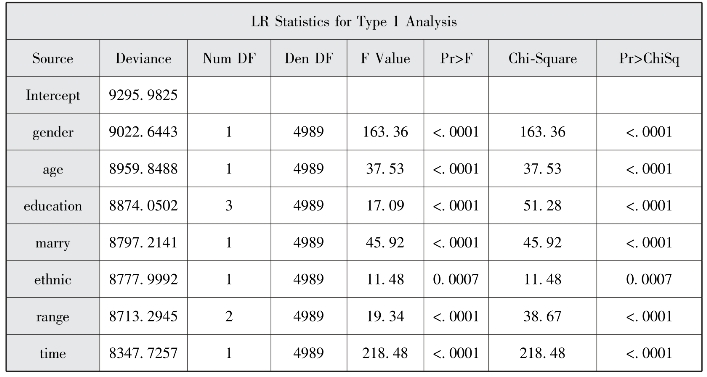
图5-5 第一型(type1)分析
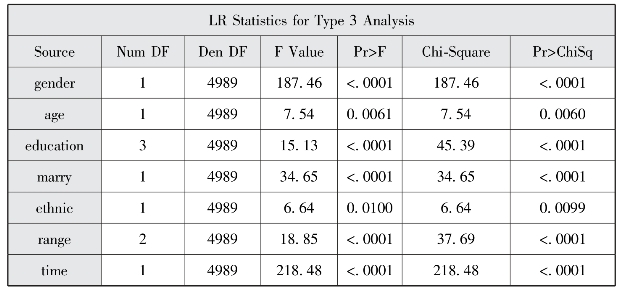
图5-6 第三型(type3)分析
SAS结果解释:
图5-1和图5-2为第一个proc genmod过程的输出结果。图5-1给出了模型信息,包括数据集名称、误差分布、链接函数形式、因变量、观测数等。图5-2输出Lagrange乘子统计量的结果。当在model语句中定义了dist=nb noscale选项时,Lagrange乘子统计量将被计算,检验Poisson回归模型中是否存在过离散现象。这里检验统计量χ 2=321.3102,p<0.0001,拒绝原假设,即拒绝数据不存在过离散的假设,也就是说该数据存在过离散,此时若继续使用Poisson回归拟合该数据,则应该对过离散进行校正。其校正方法有很多,直接进行负二项回归分析就是其中一种,或者还可以采用相应的方法对过离散参数进行估计(对过离散参数进行估计的方法很多,具体可参见相关著作)。进行Poisson回归分析时,参数的点估计值不会受过离散参数大小的影响,但是参数估计的标准误和置信区间则会受其影响。在SAS中我们可以通过“scale=deviance”或者“scale=pearson”对过离散参数进行估计。需要注意的是,数据过离散现象产生的原因有很多,比如数据中有异常值存在,又或者是有重要的解释变量未被纳入模型等,因此,在选择模型对数据进行拟合时,需要仔细考虑数据的实际情况。
图5-3到图5-6为第二个proc genmod过程的输出结果。图5-3显示了模型拟合优度检验的结果。包括偏差统计量、尺度化的偏差统计量、χ2值、尺度化的χ2值和相应的自由度以及对数似然值等,并显示计算收敛。关于此模型对数据资料的拟合效果,暂不评价,需要与其他同类模型的拟合结果进行比较,才能得出有说服力的判定。
图5-4给出了参数估计的结果,包括参数估计值、标准误、95%置信区间、参数检验卡方值和p值。该模型显示,尺度参数由“1”调整为“1.2935”,由此模型中各参数的标准误均得到校正,经校正后,结果显示不同性别、年龄、大专及以上学历、婚姻状况、民族、流动范围、流动时间的流动次数差异具有统计学意义(p<0.05)。模型系数解释其实与Logistic回归系数的解释类似,比如性别的系数为-0.5132,可以解释为女性流动到其他城市的次数是男性的0.60倍(e-0.5132≈0.60)。
图5-5和图5-6分别给出了type1和type3分析的似然比统计量。第一型分析中,当引入性别因素时,偏差统计量为9022.6443,再引入年龄、受教育程度、婚姻状况、民族、流 动 范 围、流 动 时 间 时 分 别 为8959.8488、8874.0502、8797.2141、8777.9992、8713.2945、8347.7257,偏差统计量逐渐缩小,模型的差别均有统计学意义。在第三型的分析中,对各因素进行假设检验的结论与第一型的分析是一致的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




