我们使用表14-1中的数据进行操作演示。首先在Excel中将数据整理如表14-2所示的格式。
表14-2 中国城镇居民年龄-时期别死亡率(1990—2010年)
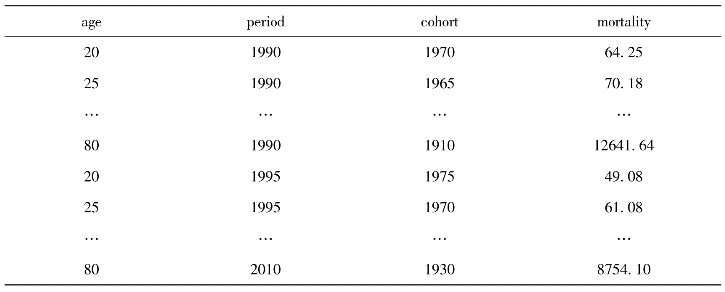
我们首先采取数据驱动的方式来确定合适的约束条件,即首先运行年龄-时期(ageperiod,AP)、年龄-队列(age-cohort,AC)及时期-队列(period-cohort,PC)模型,帮助我们确定哪两个虚拟项的估计系数最相近。首先将Excel数据导入数据,并对年龄、时期和队列进行虚拟变量编码,最后运行具体的AP模型。这里我们使用广义线性模型(generalized linear model,GLM),假设死亡率这一结局变量服从泊松分布。本节及随后两小节所用数据库均为exe14_1。
SAS程序:
data exe14_1;set work.exe14_1;
if cohort=1910 then cohort_1910=1;else cohort_1910=0;
if cohort=1915 then cohort_1915=1;else cohort_1915=0;
if cohort=1920 then cohort_1920=1;else cohort_1920=0;
if cohort=1925 then cohort_1925=1;else cohort_1925=0;
if cohort=1930 then cohort_1930=1;else cohort_1930=0;
if cohort=1935 then cohort_1935=1;else cohort_1935=0;
if cohort=1940 then cohort_1940=1;else cohort_1940=0;
if cohort=1945 then cohort_1945=1;else cohort_1945=0;
if cohort=1950 then cohort_1950=1;else cohort_1950=0;
if cohort=1955 then cohort_1955=1;else cohort_1955=0;
if cohort=1960 then cohort_1960=1;else cohort_1960=0;
if cohort=1965 then cohort_1965=1;else cohort_1965=0;
if cohort=1970 then cohort_1970=1;else cohort_1970=0;
if cohort=1975 then cohort_1975=1;else cohort_1975=0;
if cohort=1980 then cohort_1980=1;else cohort_1980=0;
if cohort=1985 then cohort_1985=1;else cohort_1985=0;
if cohort=1990 then cohort_1990=1;else cohort_1990=0;
if period=1990 then period_1990=1;else period_1990=0;
if period=1995 then period_1995=1;else period_1995=0;
if period=2000 then period_2000=1;else period_2000=0;
if period=2005 then period_2005=1;else period_2005=0;
if period=2010 then period_2010=1;else period_2010=0;
if age=20 then age_20=1;else age_20=0;
if age=25 then age_25=1;else age_25=0;
if age=30 then age_30=1;else age_30=0;
if age=35 then age_35=1;else age_35=0;
if age=40 then age_40=1;else age_40=0;
if age=45 then age_45=1;else age_45=0;
if age=50 then age_50=1;else age_50=0;
if age=55 then age_55=1;else age_55=0;
if age=60 then age_60=1;else age_60=0;
if age=65 then age_65=1;else age_65=0;
if age=70 then age_70=1;else age_70=0;
if age=75 then age_75=1;else age_75=0;
if age=80 then age_80=1;else age_80=0;
proc genmod;
model mortality=age_25 age_30 age_35 age_40 age_45 age_50 age_55 age_60 age_65 age_70 age_75 age_80 period_1995 period_2000 period_2005 period_2010/dist=poisson link=log;(https://www.xing528.com)
run;
SAS程序解释:
proc genmod表示我们使用广义线性模型进行模型拟合,dist=poisson表示结局变量服从泊松分布,link=log表示链接函数为log函数。上述模型舍去了年龄和时期的第一项,表明我们选择它们作为各自因素的参照项,可以由研究者自由选择舍去哪个项作为参照项(如果不舍去,则模型将会默认各因素的最后一项为参照项)。
SAS结果:
SAS结果输出如下:
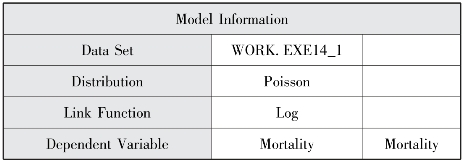
图14-1 AP模型基本信息

图14-2 AP模型拟合信息

图14-3 AP模型估计结果
SAS结果解释:
图14-1显示该模型选择的结局变量及其分布类型,以及所使用的链接函数是什么。图14-2给出了多个拟合指数值。最后图14-3的结果估计部分显示了最大似然(maximum likelihood,ML)估计的结果(ML估计为系统默认估计方法),并给出了各个变量的估计值及对应的标准误、95%置信区间、p值等信息。很显然,此时年龄和时期效应均具有统计学意义。
按照上述步骤,我们继续运行AC和PC模型(对应的SAS程序与上面的AP模型类似在此不做展示),得到相应结局。我们将三种模型得到的年龄、时期和队列效应用折线图的方式进行呈现,具体见图14-4。

图14-4 AP、AC、PC模型中年龄、时期和队列估计系数图
我们知道,成年人的死亡率会随着年龄的增长而加速增长,且相对于时期和队列因素,个体衰老因素对于该生理性指标的影响无疑是最大的。以该比较可靠的专业知识为依据,我们知道PC模型对队列效应的估计有较大的偏倚,因为其得到的队列效应远强于AP和AC模型得到的年龄效应。我们以AP和AC模型为依据,得到队列1941—1945(-0.7859)和队列1946—1950(-0.7796)的估计系数相差最小,因此设定这两项的估计效应相等。下面利用SAS来运行APC一般约束估计的全模型。
SAS程序:
proc genmod date=exe 14_1;
model mortality=age_25 age_30 age_35 age_40 age_45 age_50 age_55 age_60 age_65 age_70 age_75 age_80 period_1995 period_2000 period_2005 period_2010 cohort_1910 cohort_1915 cohort_1920 cohort_1925 cohort_1930 cohort_1935 cohort_1940 cohort_1955 cohort_1960 cohort_1965 cohort_1970 cohort_1975 cohort_1980 cohort_1985 cohort_1990/dist=poisson link=log;
run;
SAS结果:
SAS结果输出如下:

图14-5 APC全模型拟合信息


图14-6 APC全模型估计结果
我们同样用折线图的形式来展示上述系数,如图14-7所示。浅虚线形式的队列效应线是将第一个队列组作为参照项(其值为零)得到的,即将点实线队列效应线向下平移使第一个队列组为零,这样更加方便我们的观察。正如我们所知道的,死亡率的年龄效应最强,死亡风险随着年龄的增长而不断上升。队列效应也十分重要,死亡风险整体上随着队列的推移而下降。时期效应比较平稳,时期系数无统计学意义。
进一步的,我们对上面运行的所有四种模型的拟合指数进行简单的比较,结果见表14-3。很明显,一般约束估计的APC全模型的AIC和BIC值最小,且对数似然值的绝对值以及偏差自由度之比也是最小的,具有最好的拟合优度。

图14-7 APC一般约束估计模型中年龄、时期和队列估计系数图
表14-3 四种模型的拟合指数比较

注:AIC赤池信息准则,BIC贝叶斯信息准则。
此外,我们还可以进一步挖掘每个因素能够解释结局变量的方差是多少。可以将死亡率进行对数转化(因为链接函数是对数函数),再使用一般最小二乘法(ordinary least squares,OLS)来对上述四种模型进行约束估计,这样可以得到每个模型的R2值。下面运行一般约束估计的APC全模型。
SAS程序:
proc reg;
model Ln_Mortality=age_25 age_30 age_35 age_40 age_45 age_50 age_55 age_60 age_65 age_70 age_75 age_80 period_1995 period_2000 period_2005 period_2010 cohort_1910 cohort_1915 cohort_1920 cohort_1925 cohort_1930 cohort_1935 cohort_1940 cohort_1955 cohort_1960 cohort_1965 cohort_1970 cohort_1975 cohort_1980 cohort_1985 cohort_1990;
run;
上述程序得到APC全模型的R2为0.9994。同理,运行AP、AC和PC模型,得到R2分别为0.9977、0.9984和0.9968。我们可以算出,年龄能够解释死亡率对数值0.26%的方差(=0.9994-0.9968),时期能够解释死亡率对数值0.10%的方差,而队列能够解释死亡率对数值0.17%的方差。注意,这里与各因素相关的特异方差(unique variance)比较小,是因为这里的特异方差只包含了其非线性效应的部分(O'Brien,2015)。
此外,我们还可以对最小二乘估计和广义线性估计所得到的一般约束估计的APC全模型进行简单的比较。我们将得到的估计效应画到图14-7中,得到虚线和实线,发现两种方法所得到的估计系数走势相似程度较高。由于链接函数的存在,两种方法所得估计系数的实际含义是稍不同的,如果将其进行适当转化,其结果应当是一致的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




