模型假设检验：多元统计分析与SAS实现

模型假设检验的目的是检验整个模型是否有统计学意义以及单个回归系数是否为零。常用的检验方法有似然比检验（likelihood ratio test，LR）、Wald检验和比分检验（score test）。

1.似然比检验

假设检验的零假设H0为：β1＝β2＝…＝βi＝0，基本思想是比较两种不同假设条件下的对数似然函数值差别的大小。具体方法是：（1）先拟合不包含影响因素的Logistic模型，求对数似然函数值ln L0。（2）再拟合包含影响因素的Logistic模型，求另一个对数似然函数值ln L1。（3）比较两个对数似然函数值差别的大小。若2个模型分别包含m个自变量和n个自变量，则似然比统计量LR＝－2（ln Lm－ln Ln），当样本量较大时，在H0成立的条件下，LR近似服从自由度为v＝m－n的χ2分布。而如果只对一个回归系数（或一个自变量）进行检验，则自由度为1。在似然比检验中，若p值小于0.05，则拒绝原假设。通过比较不加入与加入i个自变量两种不同假设条件下的对数似然函数值，看其差别大小，判别新加入的i个自变量是否有统计学意义。

2.比分检验

以未包含某个或几个变量的模型为基础，保留模型中参数的估计值，并假设新增加的参数为零，计算似然函数的一价偏导数（也称“有效比分”）及信息矩阵，两者相乘便得比分检验的统计量S。样本量较大时，S近似服从自由度为影响因素个数的χ2分布。(www.xing528.com)

3.Wald检验

即用μ检验或χ2检验来检验各参数βi是否为0，也可以视为广义的t检验。进行假设检验的统计量为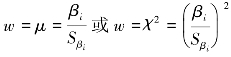，其中Sβi是偏回归系数βi的标准误。当零假设H0：β1＝β2＝…＝βi＝0为真时，w服从自由度为1的渐近χ2分布，对于大样本资料，在零假设下w近似服从标准正态分布。

上述三种假设检验中，似然比检验最可靠，既适合单个自变量的假设检验又适合多个自变量的同时检验。Wald检验在计算和使用上更容易一些，但是结果略偏于保守，它未考虑各变量的综合作用，当变量间存在共线性时，结果不可靠。在小样本情况下，比分检验统计量的分布比似然比检验统计量更接近χ2分布，犯一类错误的概率小一些。在大样本情况下，使用三种方法得到的结论一般相同。假设检验统计量的计算结果同样会在SAS程序的结果中提供。