【摘要】:,i)的作用下发生的概率为P,不发生的概率为1-P,则Logistic回归模型定义为:其中β0称为常数项或截距,β1,β2,…,βi称为Logistic模型的回归系数。从Logistic回归模型的定义公式(4-1)可以看出,Logistic回归模型是一个概率型非线性模型,当β0+β1 x1+β2 x2+…图4-1Logistic函数的图形为了方便理解和解释Logistic回归模型的意义,我们可以将公式(4-1)转换为自变量的线性表达模式。
设某事件y在影响因素xi(i=1,2,3,…,i)的作用下发生的概率为P,不发生的概率为1-P,则Logistic回归模型定义为:
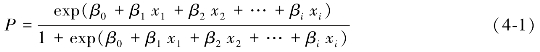
其中β0称为常数项或截距,β1,β2,…,βi称为Logistic模型的回归系数。从Logistic回归模型的定义公式(4-1)可以看出,Logistic回归模型是一个概率型非线性模型,当β0+β1 x1+β2 x2+…+βi xi在(-∞,+∞)间变化时,P在区间(0,1]之间变化,β0+β1 x1+β2 x2+…+βi xi和P的关系如图4-1所示,其中自变量xi可以任意取值,自变量的类型可以是数值变量,也可以是分类变量,从而满足了实际问题中不同变量的取值要求。

图4-1 Logistic函数的图形
为了方便理解和解释Logistic回归模型的意义,我们可以将公式(4-1)转换为自变量的线性表达模式。(https://www.xing528.com)
首先,定义事件发生概率与事件不发生概率的比为事件发生比(odds),表达式为:

那么,将公式(4-2)两边同取对数,就可以得到概率的函数与自变量之间的线性表达式:
![]()
需要注意的是,经过转换之后的公式(4-3),等式左边的取值范围由原来的(0,1]变为了(-∞,+∞)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




