在纵向数据中，个体为水平2单位，个体的重复测量为水平1单位。限于篇幅，我们仅示范多层二分类变量Logistic回归模型在纵向数据中的应用。本节我们还是使用数据集exe 13，结局测量为在每次的测量中儿童是否超重。具体使用的变量如下。
结局变量：
w：是否超重，二分类变量（根据BMI＞24划分为两类，1为超重，0为不超重）。
水平1解释变量：在发展模型中，水平1解释变量是随时间而变化的研究对象个体内测量，在本研究中包括：
time：调查时间，对1991年、1993年、1997年、2000年、2004年、2006年、2009年、2011年和2015年分别编码为：0、2、6、9、13、15、18、20。
水平2解释变量：在发展模型中，水平2解释变量是不随时间而变化的研究对象个体间测量，数据包括：
age：连续变量，为基线调查时的年龄。
gender：性别（1＝男，0＝女）；
weight：基线调查时是否超重（1＝超重；0＝不超重）
我们假设个体协变量仅对是否超重发生比的初始水平有影响，采用多层模型-随机模型可表达为：
组合模型为：
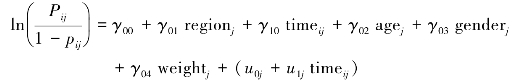
SAS程序：
proc glimmix data＝exe13 method＝rspl；(www.xing528.com)
class idind；
model w(event＝ˈ1ˈ)＝time region mean＿age gender weight/s dist＝binary link＝logit ddfm＝bw；
random int time/subject＝idind type＝vc；
nloptions tech＝nrridg；
run；
SAS程序解释：
proc glimmix程序与proc mixed语句非常相似，该程序默认的参数估计法method是限制性/残差虚拟似然法（restricted/redidual pseudo likelihood，RSPL），method选项也可设定为ML估计法，如laplace。在model语句中，设定二分类结局变量后，括号内选项
指定分析结局变量w＝1的概率。选项dist＝binary允许我们选择二分类结局测量的具体类别的概率，本例中计算的是w＝1的概率。link＝logit选项设定模型的连接函数为Logit连接函数。ddfm＝bw设定为betwithin方法将残差自由度分解为组间自由度和组内自由度。random语句中的type选择用于指定在估计随机效应时使用的协方差结构，我们使用了type＝VC选项，这是SAS中的默认选项，也是最简单的结构，当指定随机效应时，协方差结构会很快变得非常复杂。因此，在估计随机截距和斜率模型时，我们需要检查日志——接收“非正定G－matrix”错误并不少见。当这种情况发生时，随机效应的结果是无效的，模型的协方差部分需要简化（Mihaela，2015）。最后nloptions语句中的tech选项可设定不同的非线性参数估计化技术。
SAS结果：
SAS部分结果如下：
图13-32 协方差参数估计
图13-33 固定效应估计值
SAS结果解释：
图13-33结果显示，变量region的效应为0.1219，表示城市儿童在初始水平的超重率与比农村儿童高，但是没有统计学差异（p＞0.05）；变量time的效应为0.1937（p＜0.05），表示随着时间推移，儿童超重概率增加，年龄越大（0.1124，p＜0.05），超重概率越大；男孩的超重概率比女孩高（0.2452，p＜0.05）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
