为了更好地区分加入交互和未加交互的线性回归区别,本节先做未加交互的线性回归,再做加入交互的线性回归模型,并分别进行分析解释。本章所用的数据来自于2018年湖北省流动人口监测数据。因变量选择流动人口接受健康教育的数量(过去一年,您在现居住社区/单位是否接受过✕✕(教育内容)的健康教育?是=1,否=0,最后将所有类别健康教育的项目相加,得到教育健康项目的数量),形成新的变量。
数据分析目的:分析收入、流动时间和年龄对接受健康教育数量的影响。
因变量:
health:流动人口接受健康教育的数量
自变量:
age:年龄
flow:流动人口的流动时间
logincome:log(家庭月收入),将家庭月收入变量变换为自然对数
gen:性别(1=男,0=女)
range:流动范围(1=跨省,2=省内跨市,3=市内跨县,4=跨境)
此处我们用SAS程序进行多元线性回归分析,导入数据库并命名为exe3_1,在运行线性回归之前,注意到解释变量中有分类变量range,这时,我们需要将其设置为哑变量,在SAS程序中可以通过以下程序设置哑变量。
SAS程序:
data exe3_11;
set exe3_1;
if range=2 then x2=1;else x2=0;
if range=3 then x3=1;else x3=0;
if range=4 then x4=1;else x4=0;
run;
这样在新的数据集exe3-11中新生成了x2,x3,x4变量,为range的哑变量,以range变量中“跨省”为参照项。随后,再运用proc reg语句来进行多元线性回归。
SAS程序:
proc reg data=exe3_11;
model health=age flow logincome sex{x2 x3 x4};
run;
SAS结果:
SAS结果输出如下:

图3-1 观测变量

图3-2(a) 方差分析

图3-2(b) 方差分析(https://www.xing528.com)

图3-3 参数估计
SAS结果解释:
上面的结果中,图3-1显示有5000个观测值被读入,4991个观测值被纳入分析,结果变量中有9个观测值缺失;图3-2(a)显示回归方程显著,F=8.28,p<0.0001,提示因变量和自变量之间存在线性相关。另外,图3-2(b)显示误差方差估计值为:1.8799;R2=0.0115与调整R2=0.0101,表示拟合优度,因变量观测值的总变异中能够由模型解释的部分所占的比例为1.01%,也就是样本方差中能够被OLS回归线所解释的部分,说明回归方程的拟合程度较差。图3-3显示了回归系数的估计值,年龄的偏回归系数为-0.0086(p=0.0026),收入的偏回归系数为-0.1870(p=0.1099),流动时间的偏回归系数为0.0079(p=0.0804),这提示在α=0.05的水平上,年龄与健康教育项目数量存在线性关系。年龄的系数可解释为在保持其他变量不变的情况下,年龄每增长1岁将使得因变量健康教育项目数量减少0.0086,由于收入与流动时间对因变量的影响不显著,所以可以将不显著的解释变量从模型中剔除。当自变量是分类变量时,不能再按照连续变量的方法进行解释。以此节硏究中的性别变量为例,在录入数据时,我们将女性录入为0,男性录入为1。SAS自动默认是以0组为参照,将1组与0组迸行对比,即将男性与女性进行对比。性別变量的系数是指这男女之间因变量预测值的差异。此节的硏究中,性别的系数是0.0537,提示男性的流动人口接受健康教育数量的预测值比女性高0.0537(控制了其他自变量),但没有统计学意义(p=0.3188)。另外,在控制其他变量后,省内跨市的流动人口接受健康教育数量的预测值比跨省流动的低0.1592(p=0.0140)。同理可以得到省内跨县和跨境的解释,这里不再赘述。截距项对应的系数在0.05下显著,但实际上,我们并不关注回归的截距,需要关注的只有自变量的系数。
下面我们用三个连续的预测变量或主效应及其双向交互作用拟合模型。因为我们有三个主效应,所以存在三种可能的双向交互:age*flow,age*logincome,flow*logincome,但在此次研究中,我们假设年龄越大,其对健康重视程度越高,接受的健康教育项目数量也会越高,同时,收入越多,其对健康重视程度越高,接受的健康教育项目数量也会越高,age和logincome,可能会存在交互。所以接下来将模型中加入交互项。
SAS程序:
data exe3_12;
set exe3_11;
age_logincome=age*logincome;
run;
结果可在exe3_12数据集中发现生成了一列age_logincome新变量,即表示x1 x2交互项,然后再将新生成的交互项变量放入到程序中。
SAS程序:
proc reg data=exe3_12;
model health=age flow logincome age_logincome sex{x2 x3 x4};
run;
SAS结果:
SAS结果输出如下:

图3-4 观测变量
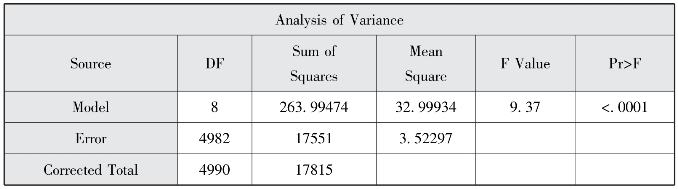
图3-5(a) 方差分析

图3-5(b) 方差分析

图3-6 参数估计
SAS结果解释:
图3-5(a)显示回归方程显著,F=9.37,p<0.0001,提示因变量和自变量之间存在线性相关。图3-5(b)表示误差方差估计值为:1.8769;R2=0.0148与调整R2=0.0132,因变量观测值的总变异中能够由模型解释的部分所占的比例为1.32%。图3-6显示了回归系数的估计值,年龄的偏回归系数为-0.1556(p<0.001),收入的偏回归系数为-1.6746(p<0.001),流动时间的偏回归系数为0.0083(p=0.0687),年龄和收入交互项的偏回归系数为0.0391(p<0.001),在α=0.05的水平上,年龄、收入与健康教育项目数量存在显著关系;在控制其他变量后,省内跨市的流动人口接受健康教育数量的预测值比跨省流动的低0.1533(p=0.0178),市内跨县的流动人口接受健康教育数量的预测值比跨省流动的高0.2917(p<0.0001),同理可以得到跨境的解释,这里不再赘述。截距项对应的系数为8.7788(p<0.001)。可以由此写出回归方程的表达式:

对于交互项的解释,年龄*收入的偏回归系数为0.0391(p<0.001),表明交互效应的存在。其系数可以从两个方面解释:第一,随着收入增加,年龄对健康教育项目数量的影响更加显著,收入每增加1个单位,年龄对健康教育项目数量的影响为-0.1165(-0.1165=-0.1555+0.0390)。第二,随着年龄的增加,收入对健康教育项目数量的影响会更加显著,年龄每增加一岁,收入对健康教育项目数量的影响为-1.6355(-1.6355=-1.6746+0.0391)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




