以人均GDP(x)作为协变量来衡量社会经济发展水平,选用生育率(y)为因变量来衡量各省市的生育水平。笔者选取了我国15个省级行政区,根据发展水平的高低划分为高、中、低三个水平,每个水平有5个代表行政区。通过协方差分析方法,检验在消除经济发展对生育率的影响后,不同发展水平地区的生育率是否存在显著差异。数据如表2-8所示。
表2-8 2005年人均GDP及生育率
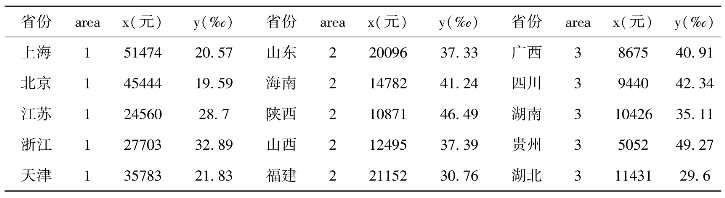
注:原始数据源来源于《中国卫生健康统计年鉴》(2006年)。
本节数据集命名为exe2_4,在SAS程序中导入数据集。涉及的变量有:
因变量:
y:表示生育率(‰)
协变量:
x:表示人均GDP(元)
控制变量:
area:地区发展程度(1=发展高水平地区,2=发展中等水平地区,3=发展低水平地区)
SAS程序:
data exe2_4;set work.exe2_4;
proc sort;
by area;
run;
proc univariate normal;
var y;
by area;
run;
proc discrim pool=test;
class area;
var y;
run;
proc sort;
by area;
run;
proc reg;
model y=x;(https://www.xing528.com)
by area;
run;
proc glm;
class area;
model y=x area;
run;
SAS程序解释:
proc univariate normal过程步检验在效应因子的每一个水平上,因变量y是否服从正态分布,proc discrim pool过程步(g>2)做方差齐性检验。proc reg过程步检验在效应因子的每一个水平上,因变量y和自变量x是否呈线性关系。proc glm调用glm过程做协方差分析,class c定义分组变量为area,model y=x c定义模型,分析area和x对y的影响。
SAS结果:
SAS结果如下:
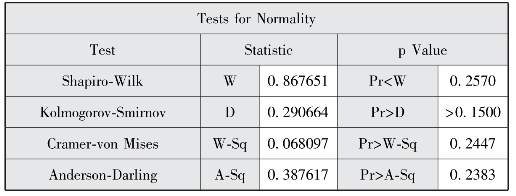
图2-7(a) 发展高水平地区数据正态性检验结果
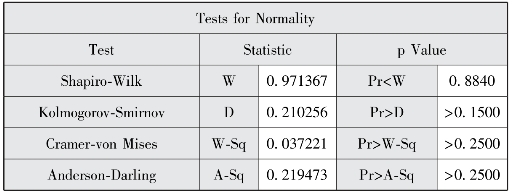
图2-7(b) 发展中等水平地区数据正态性检验结果
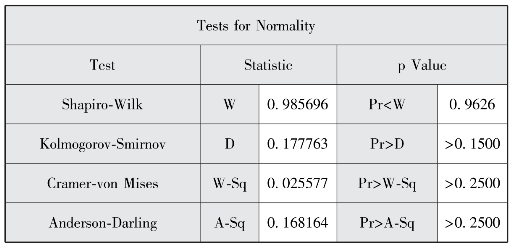
图2-7(c) 发展低水平地区数据正态性检验结果
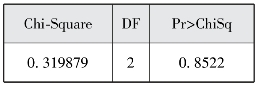
图2-8(a) 方差齐性检验结果
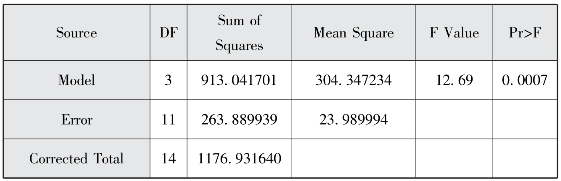
图2-8(b) 方差齐性检验结果
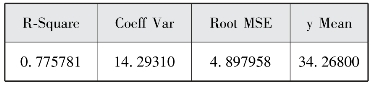
图2-8(c) 方差齐性检验结果
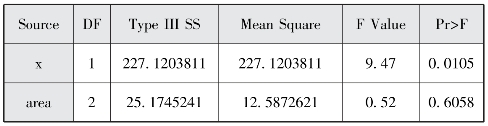
图2-8(d) 方差齐性检验结果
SAS结果解释:
图2-7(a)到图2-7(c)说明三组数据正态性检验结果均服从正态分布,图2-8(a)显示方差齐性检验结果符合方差齐性(F=0.3198、p=0.8522)。
图2-8(b)显示总体方差检验得到F=12.69,p<0.05,可以认为三个地区之间生育率存在显著差异。根据Type III SS定义,检验模型中每一个自变量时,都校正模型中的其他自变量对y的影响。图2-8(d)表明,在校正了人均GDP对生育率的影响之后,不同发展水平地区生育率没有显著性差异(p=0.6058)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




