多元方差分析(multivariate analysis of variance,MANOVA),亦称为多变量方差分析,即表示多元数据的方差分析,是一元方差分析的推广。当因变量(结果变量)不止一个时,可用多元方差分析对它们同时进行分析。作为一个多变量过程,多元方差分析将多个因变量看作一个整体,分析因素对于多个因变量的整体影响,发现不同总体的最大组间差异。多元方差分析是单变量方差分析的推广形式,同样也用于检验不同样本间是否存在显著差异(Groenen&Meulman,2004)。与单变量方差分析不同,多元方差分析不仅只考虑一个因变量,而是同时建立在多个因变量观测值之上,这也是与一元多因素方差分析最重要的区别。
多元方差分析法对于分析的数据有一定要求:自变量的各个组内,各因变量之间存在线性关系且要求较大的总样本量。此外,使用多元方差分析进行分析时,还需要考虑以下假设:(1)数据来自随机样本,各观察对象之间相互独立。(2)各因变量服从多元正态分布,多元正态分布指的是多个因变量之间的正态分布,它与单因变量正态分布在形式上尽管不同,但有很多相似之处,实际上是单因变量正态分布在多维上的推广。(3)样本量尽量足够大。(4)各因变量之间存在线性相关关系。(5)各组观察对象因变量的方差-协方差矩阵相等,即方差齐性。协方差矩阵计算的是不同因变量之间的协方差:

假设数据集有三个响应变量{x,y,z},则协方矩阵为:
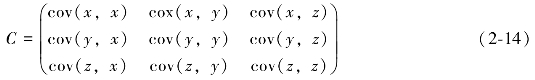
协方差矩阵是一个对称的矩阵,而且对角线是各个因变量的方差。协方差矩阵的球形性是指该对角线元素(方差)相等、非主对角线元素(协方差)相等(王学仁,1986)。

对于多元方差分析,假设有i个因变量,j个处理因素水平,则其统计原假设的向量形式如下:
 (https://www.xing528.com)
(https://www.xing528.com)
即多组均向量是否相同的检验。
多元方差分析的基本思想与一元方差分析的基本思想一致,离差平方和与离差积和矩阵(total sum of squares and cross products matrix,SSCP),其实就是ANOVA中SS总 在多元中的对应量。SSCP矩阵T是每个实验单元i个因变量所组成的向量与总平均向量之差,乘以此差的转置阵,最后求和。

其中g为自变量水平数;ni为每组处理中样本个数。
根据公式推导可对离差平方和与离差积和矩阵公式进行分解,最后可得:SSCP=H(组间矩阵)+E(组内矩阵);N=n1+n2+…+ni
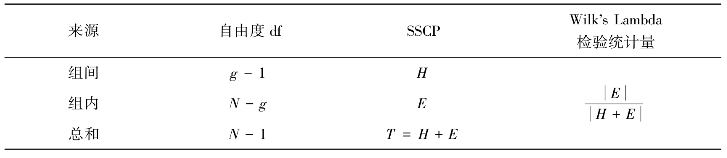
在多元方差分析中有四个检验统计量,分别是:(1)Pillai's Trace:值越大,表明该效应项对模型的贡献越大。(2)Wilks'Lambda:取值范围在0~1,值越小,说明该效应项对模型的贡献越大。(3)Hotelling-Lawley's Trace:检验矩阵特征根之和,其值总是比Pillai's Trace的值大。与Pillai's Trace相似,值越大贡献越大。(4)Roy's Largest Root:为检验矩阵特征根中最大值,因此它总是小于或等于Hotelling-Lawley's Trace。当模型建立的前提条件不满足时,Pillai's Trace最为稳健。Pillai's Trace、Wilks'Lambda、Hotelling-Lawley's Trace和Roy's Largest Root作为四个多元统计量,可用于检验组间差异。其中,最常用的统计量为Wilks'Lambda,该检验p<0.05时,自变量的组间差异具有统计学意义。如表2-6所示。
表2-6 多元方差分析分解表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




