多因素方差分析的实现（SAS）

2.2.2.1　多因素方差分析简介

在研究中，单因素方差分析只着眼于单独的某个因素对于因变量的影响，但由于诸多条件因素的限制，还会有很多其他因素无法控制，并且大多数研究者也不仅仅满足于单因素的方差分析。在本节，我们将介绍多因素方差分析，它是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析，也用于检验不同水平组合之间因变量均数受不同因素影响是否有差异。在多因素方差分析过程中可以分析每一个因素的作用，可以分析因素之间的交互作用，也可以分析协方差，以及各因素变量与协变量之间的交互作用。同样地，多因素方差分析要求因变量来源于正态分布总体并相互独立，且相互比较的各样本总体方差相等。

以下述表2-5的数据为例，分析2000年与2010年我国部分地区人口平均预期寿命差异，这时观测值可表示为yijk，它表示第i个地区第j年第k个省的人口平均预期寿命，可将其分解为（王松桂，1999）：

这里μ表示总的平均值，αi表示第i个地区的影响效应，βj表示第j年的效应，εijk是随机误差。此例中，i＝1，2，3；j＝1，2；k＝1，2，3，4，问题包含了两个因素：不同的地区和不同的年份。γij则表示地区和年份两因素之间的交互作用。当某因素的各个单独效应随另一因素变化而变化时，则称这两个因素间存在交互作用。

基于方差模型的基本思想，对全部数据总平方和SS总进行分解，即：

其中SSE为误差平方和，SSA为因素A的平方和，SSB为因素B的平方和，SSAB为交互作用的平方和，反映A和B的交互作用对因变量的影响。

在考虑交互作用的情况下，除了需要检验因素A、B对于因变量的影响有无显著差异：H1：a1＝a2＝…＝αa＝0；H2：β1＝β2＝…＝βb＝0，还需要检验交互效应是否存在，即检验：H3：γij＝0，i＝1，2，…，a；j＝1，2，…，b；当H3成立：

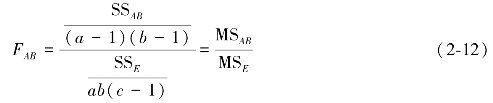
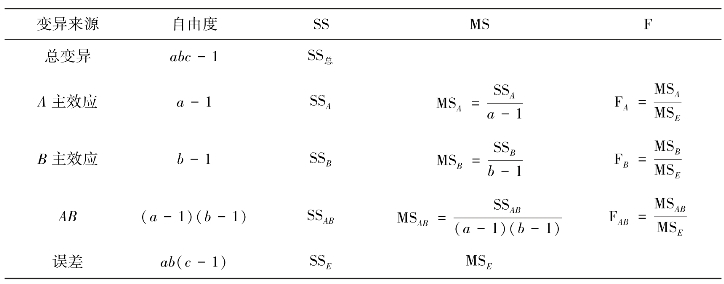
根据此统计量，可以检验H3。如果经检验接受H3，则可以认为交互效应不存在。那么此时可以进一步检验因素A或因素B的各水平效应有无显著差异。以上可以归纳成如表2-4所示的内容。

表2-4　两因素方差分析表

2.2.2.2　实例分析与SAS实现

本节通过多因素方差分析2000年与2010年我国部分地区人口平均预期寿命的差异，使用数据如表2-5所示，数据集命名为exe2＿2。

表2-5　我国部分地区人口平均预期寿命

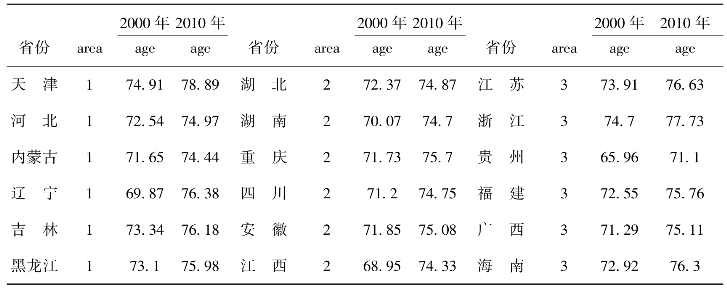
注：原始数据来源于《中国卫生健康统计年鉴》（2018年）。

因变量：

age：表示平均预期寿命

自变量：(www.xing528.com)

area：3个不同地区（1＝北部，2＝中部，3＝南部）

year：年份（1＝2000年，2＝2010年）

SAS程序：

data exe2＿2；set work.exe2＿2；

proc anova；

class area year；

model age＝area year area*year；

run；

SAS程序解释：

proc anova调用anova过程步进行方差分析，class area year定义分组变量分别为area和year；model age＝area year area*year定义模型，分析area和year对age的影响。

SAS结果：

SAS结果输出如下：

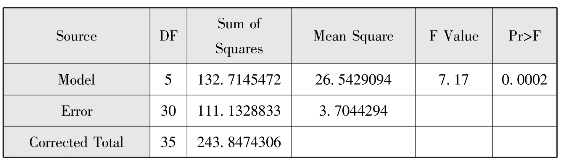
图2-4（a）　多因素方差分析总体检验结果

图2-4（b）　确定系数结果

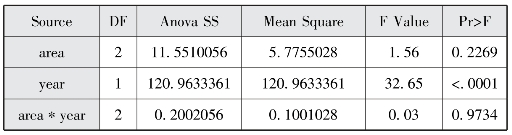
图2-4（c）　因子的主效应和交互效应检验结果

SAS结果解释：

上面的结果给出了模型的总体检验结果，p＝0.0002（p＜0.05），差异具有统计学意义，R2＝0.5443。其中，因子的主效应和交互效应检验结果为：因素year对因变量（人口平均预期寿命）的影响具有统计学显著性（p＜0.05），而与地区的交互效应（p＝0.9734）对人口平均预期寿命的影响则没有显著性影响，说明2000年与2010年人口平均预期寿命有显著性差异，但与地区无交互作用。