1.三维网格图元
三维网格图元是一种里面空心，外表为平面或是曲面包裹的模型。执行“绘图”→“建模”→“网格”→“图元”命令，弹出如图5-34所示的子菜单，在弹出的子菜单中选择相应的三维网格图元。或选择“网格”选项卡，在对应的“图元”面板上直接单击进行选择，如图5-35所示。
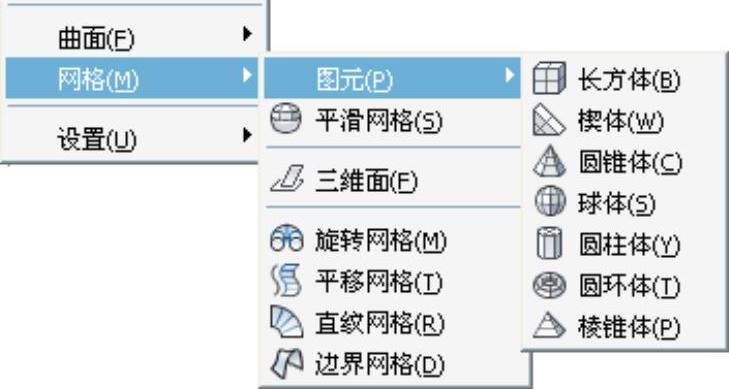
图5-34 “平滑网格图元”子菜单
图5-35 “图元”面板
（1）网格长方体
单击“网格长方体”命令按钮
，操作如下：
结果如图5-36所示。
提示：
图中网格长方体的显示样式是二维线框模式，在后面所介绍的三维曲面建模模型都是以二维线框模式显示。
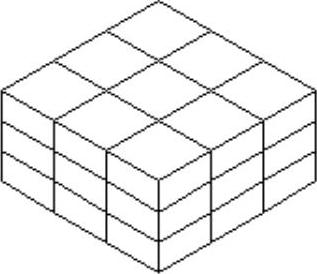
图5-36 网格长方体
（2）网格圆锥体
单击“网格圆锥体”命令按钮
，操作如下：
结果如图5-37所示。
（3）网格圆柱体
单击“网格圆柱体”命令按钮
，操作如下：
结果如图5-38所示。
（4）网格棱锥体
单击“网格棱锥体”命令按钮
，操作如下：
结果如图5-39所示。
图5-37 网格圆锥体
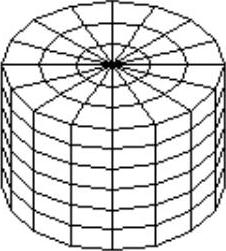
图5-38 网格圆柱体
图5-39 网格棱锥体
（5）网格球体
单击“网格球体”命令按钮
，操作如下：
结果如图5-40所示。
（6）网格楔体
单击“楔体”命令按钮
，操作如下：
结果如图5-41所示。
（7）网格圆环体
单击“网格圆环体”命令按钮
，命令与操作如下：
结果如图5-42所示。
图5-40 网格球体
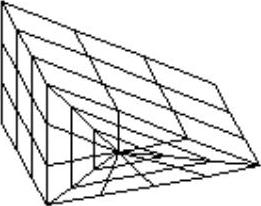
图5-41 网格楔体
图5-42 网格圆环体
2.三维多段线
与二维多段线相比，确定三维多段线的点增加了Z坐标值。在功能区中选择“曲面”选项卡。单击“三维多段线”命令按钮
，操作如下：
结果如图5-43所示。
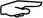提示：
将当前视图设为“西南等轴测”，在“导航”面板中选择“动态观察”，可多方位地观察此三维多段线。
3.平面曲面
单击“平面曲面”命令按钮
，操作如下：
结果如图5-44所示。
提示：
所绘制的平面曲面在由X、Y轴所确定的平面上。(www.xing528.com)
4.三维面
用户可以通过指定顶点来绘制三维面网格，其顶点数不能超过四个。执行“绘图”→“建模”→“网格”→“三维面”命令，操作如下：
结果如图5-45所示。
图5-43 三维多段线
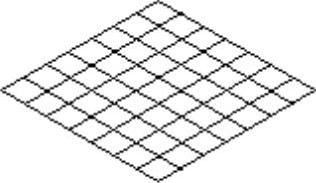
图5-44 平面曲面
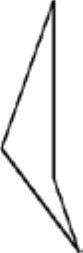
图5-45 三维面
5.矩形网格
使用矩形网格命令可以在M和N方向（类似于XY平面的X轴和Y轴）上创建开放多边形网格。在命令行内输入“3DMESH”，操作如下：
结果如图5-46所示。
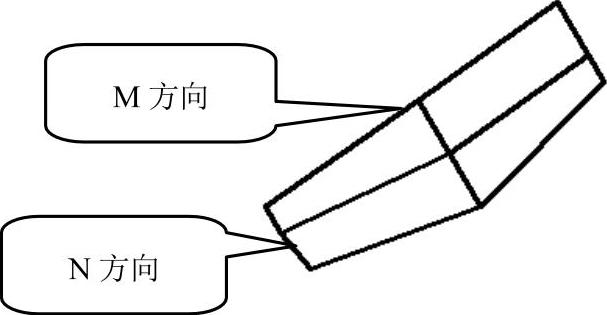
图5-46 三维网格
提示：
M和N方向网格面的顶点数在2～256取值，且为整数。
6.三维网格曲面
在功能区中选择“网格”选项卡。
（1）直纹曲面
直纹曲面是由指定的直线或曲线作为相对的两边所生成。打开源文件“例图5-47a”，单击“直纹曲面”命令按钮
，操作如下：
结果如图5-47b所示。
提示：
直纹曲面的边界可以是直线、点、圆弧、圆、椭圆、椭圆弧、二维多段线、三维多段线和样条曲线。用做直纹曲面边界的两个对象必须是全部开放或是闭合。点对象可以和开放或闭合对象成对使用，不受影响。
图5-47 直纹曲面
提示：
线框密度可通过输入SURFTAB1，SURFTAB2来进行设置。SURFTAB1（经线）可用于控制Rulesurf（直纹曲面）和Tabsurf（平移曲面）命令的网格控制点数目，也可用于Revsurf（旋转曲面）和Edgesurf（边界曲面）命令的M方向网格点数目。SURFTAB2（纬线）用于控制Revsurf（旋转曲面）和Edgesurf（边界曲面）命令的N方向网格点数目。
（2）平移曲面
平移曲面是指直线或曲线（即轨迹曲线）沿着指定的方向和距离（即方向矢量）伸展而成的曲面。打开源文件“例图5-48a”。
①使用SURFTAB1命令设置经线方向线框密度为20。
在命令行中输入“SURFTAB1”，操作如下：
②使用平移曲面命令。
单击“平移曲面”命令按钮
，操作如下：
提示：
选择直线作为方向矢量时，若选中直线上的点A，则伸展方向从A到B，如图5-48b所示；若选中直线上的点B，则伸展方向从B到A，伸展的距离为方向矢量的长度，如图5-48c所示。
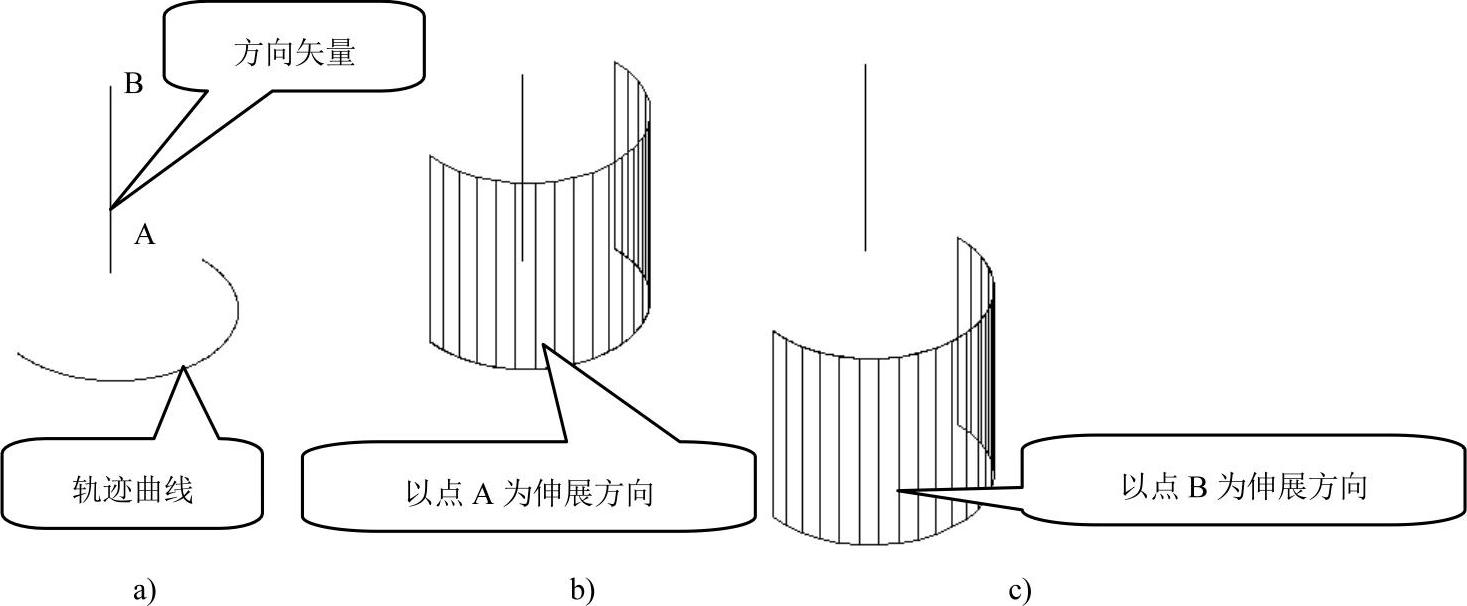
图5-48 平移曲面
（3）旋转曲面
旋转曲面命令是指一条轮廓线绕指定轴以指定角度旋转而形成的曲面。该轮廓线可以是由直线、圆、圆弧、椭圆、椭圆弧、多段线、样条曲线、闭合多段线、多边形、闭合样条曲线和圆环的任意组合组成的。旋转而成的曲面可以是封闭的，也可不是封闭的。打开源文件“例图5-49a”。
1）使用SURFTAB1命令设置经线方向线框密度为20。
在命令行中输入“SURFTAB1”，操作如下：
2）使用SURFTAB2命令设置纬线方向线框密度为20。
在命令行中输入“SURFTAB2”，操作如下：
3）使用旋转曲面命令，绘制的旋转曲面如图5-49b所示。
单击“旋转曲面”命令按钮
，操作如下：
（4）边界曲面
边界曲面是通过定义4条首尾相连的边而构成的曲面，它相当于孔斯曲面。边界可以是能够形成闭合环而且能共享端点的圆弧、直线、多段线、样条曲线或椭圆弧。打开源文件“例图5-50a”，单击“边界曲面”命令按钮
，操作如下：
结果如图5-50b所示。
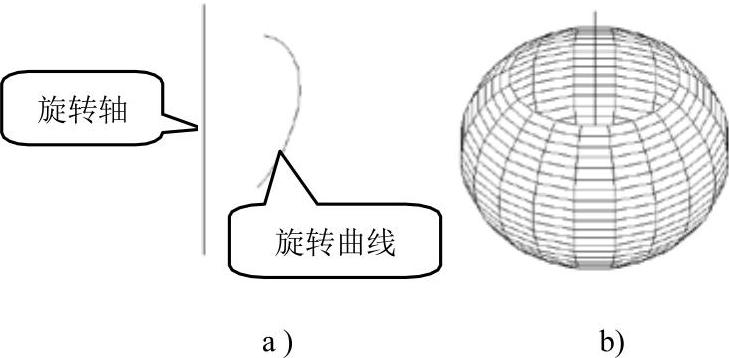
图5-49 旋转曲面
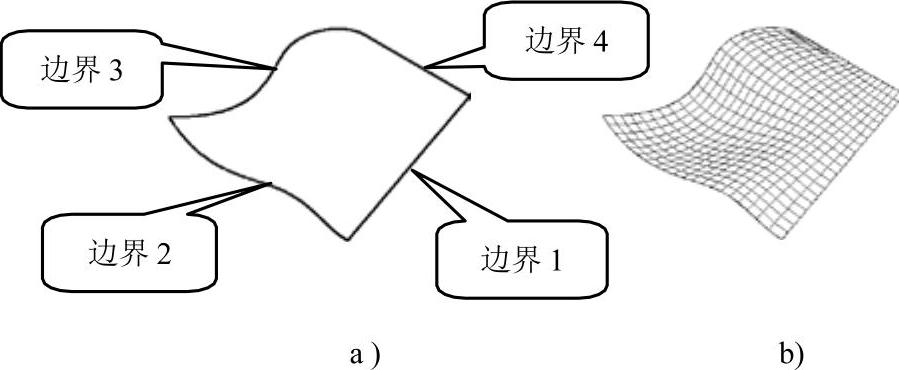
图5-50 边界曲面
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
