非线性偏微分方程的守恒律及对称性研究

这一小节，将研究方程（7.1）的守恒律。考虑下面的 Riemann-Liouville 分数阶导数

这里Dt是关于t的微分算子，n=[α]+1，0Itn−αu 定义为[132]：

这里Γ（z）是Gamma 函数.

守恒向量场满足下面的守恒方程

这里Ct=Ct（t，x，u，…），Cx=Cx（t，x，u，…）。方程（7.34）称为方程（7.1）的守恒律.

引入方程（7.1）的拉格朗日函数如下

这里v（x，t） 是新的函数，则有

欧拉拉格朗日算子定义为[132，141]

这里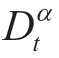（）*是（Dtα）的伴随算子.

注意到（7.1）关于Riemann-Liouville 分数阶导数可以重新写成守恒的形式

伴随方程类似于整数阶情况，所以可以得到

现在考虑含有两个自变量t，x 和一个因变量 u（t，x）的情况，则有

这里l是恒等算子，是欧拉拉格朗日算子，Nt和Nx是Noether 算子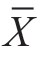，是李对称算子的延拓公式(www.xing528.com)

并且特征函数如下

算子Nt定义如下[132，141]：

这里 J是[132，141]：

算子Nx如同整数阶情况

对于X以及方程的任意解，有下面的关系

从这个等式，可以得到守恒律

下面给出方程（7.1）的守恒律。

当α ∈（0，1）时，利用（7.43）和（7.45），可以得到

这里i=1，2 和特征函数Wi是

同理，对于α ∈（1，2）的情况，可以得到

这里i=1，2并且函数Wi有下面的形式