非线性偏微分方程的对称性与不变解研究成果

首先回顾一下分数阶导数的基本概念[126，127，128]，Riemann-Liouville 分数阶导数定义如下

这里Γ（z）是Euler-gamma 函数。

类似于李群在整数阶微分方程中的应用步骤，考虑（7.1）在单参数李点变换下是不变的，则

这里∊是群参数，相应的向量场是

这里

再利用无穷小不变性准则，可以得到

这里.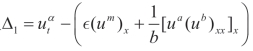

三阶延拓算子pr（α，3V） 是

这里ηx，ηxx，ηxxx 如同整数阶情况

特别是

同时

并且有额外的限制条件

相比李对称方法在整数阶非线性偏微分方程中应用而言，可以发现条件（7.11）和（7.13）对于分数阶非线性偏微分方程是十分关键的.

现在利用上面的描述，可以得到下面的定理

定理7.2.1 方程（7.1）的对称群由下面的向量场构成

证明：假定（7.1）在单参数无穷小变换群（7.3）是不变的，可以得到下面的对称方程，

将（7.8），（7.9），（7.10）代入（7.15），并且令u的不同导数项等于零，可以得到

解这些方程，可以得到

这里c1和c2是任意常数。因此，相应的向量场是(www.xing528.com)

或者

这就完成了证明.

对于V2，可以得到相应的特征方程

从而，可以得到下面的相似变量和相似变换

自然有

定理 7.2.2 变换（7.20）将（7.1）约化成下面的分数阶常微分方程

这里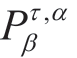是Erdelyi-Kober 分数阶微分算子[138]

其中

是Erdélyi-Kober 分数阶积分算子.

证明：首先令 n−1 < α<n，n=1，2，3，…基于Riemann-Liouville 导数和相似变换，可以得到

假定v=，（7.25）变成

利用关系，（7.26）进一步简化成

因此，可以得到

重复前面的步骤，有

因此

这样一来，可以发现（7.1）约化成下面的分数阶非线性常微分方程

这就完成了证明.