线性方程组解的结构与求解详解

8.1齐次线性方程组解的结构与求解

设A是m×n矩阵，则

（1）当r（A）=n时，齐次线性方程组Ax=0只有零解.

（2）当r（A）<n时，齐次线性方程组Ax=0有非零解.记此时基础解系为η₁，η₂，…，η_n-r（r=r（A）），则通解为

x=C₁η₁+C₂η₂+…+C_n-rη_n-r（C₁，C₂，…，C_n-r是任意常数）.

8.2非齐次线性方程组解的结构与求解

设A是m×n矩阵，b是m维非零列向量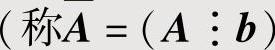为增广矩阵），则

（1）当r（A）>r（A）时，非齐次线性方程组Ax=b无解.

（2）当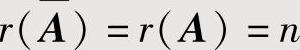时，非齐次线性方程组Ax=b有唯一解.

（3）当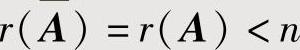时，非齐次线性方程组Ax=b有无穷多解，此时通解x=C₁η₁+C₂η₂+…+C_n-rη_n-r+x^∗（其中η₁，η₂，…，η_n-r是Ax=b的导出组Ax=0的基础解系，r=r（A），x^∗是Ax=b的一个特解，C₁，C₂，…，C_n-r是任意常数）.

例8.1（单项选择题） 设A是m×n矩阵，B是n×m矩阵，则对线性方程组（AB）x=0，下列结论必成立的是

（A）当n>m时，仅有零解. （B）当n>m时，必有非零解.

（C）当m>n时，仅有零解. （D）当m>n时，必有非零解.

[ ]

精解 （AB）x=0是m元齐次线性方程组.因为r（AB）≤min{m，n}，所以m>n时，r（AB）≤n<m.从而（AB）x=0必有非零解.

因此本题选（D）.

例8.2（单项选择题） 设A是n阶矩阵，α是n维列向量.若秩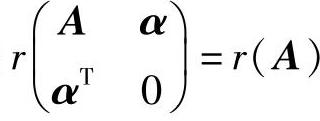，则线性方程组

（A）Ax=α必有无穷多个解.

（B）Ax=α必有唯一解.

（C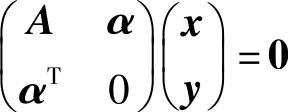）仅有零解.

（D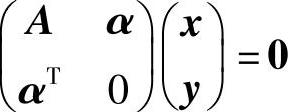）必有非零解.

[ ]

精解 由于题设中给出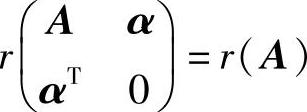，所以从考虑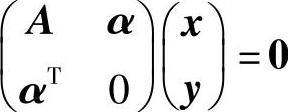入手.

由于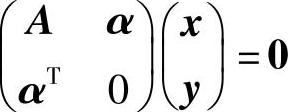是n+1元齐次线性方程组.于是由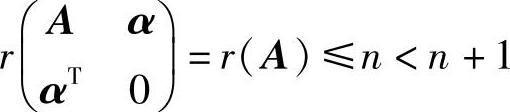知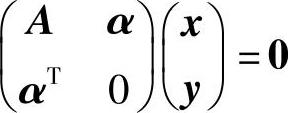必有非零解.

因此本题选（D）.

例8.3（单项选择题） 设n阶矩阵A的伴随矩阵A^∗≠O，若ξ₁，ξ₂，ξ₃，ξ₄是非齐次线性方程组Ax=b的四个互不相等的解，则对应的齐次线性方程组Ax=0的基础解系

（A）不存在. （B）仅含一个非零解向量.

（C）含有两个线性无关的解向量. （D）含有三个线性无关的解向量.

[ ](www.xing528.com)

精解 由于ξ₂-ξ₁，ξ₃-ξ₁，ξ₄-ξ₁都是Ax=0的解，所以r（A）≤n-1.于是由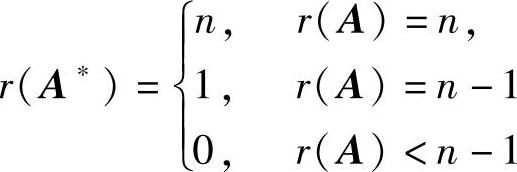，知r（A^∗）=1（由于A^∗≠O知r（A^∗）≠0），所以r（A）=n-1.

从而Ax=0的基础解系中仅含一个非零解向量.

因此本题选（B）.

例8.4 （1）已知非齐次线性方程组

有三个线性无关的解.证明方程组的系数矩阵A的秩r（A）为2，并求a，b的值.

（2）设三阶矩阵B≠O，且它的列向量都是齐次线性方程组

的解，求λ的值，并证明|B|=0.

精解 （1）由于所给的非齐次线性方程组有三个线性无关的解，记为ξ₁，ξ₂，ξ₃，则ξ₂-ξ₁，ξ₃-ξ₁都是导出组的解，且线性无关，即导出组的基础解系中至少含有两个解向量，于是有

r（A）≤4-2=2.

此外，由所给方程组知r（A）≥2.因此r（A）=2.

对A施行初等行变换：

于是由r（A）=2得

（2）由于B≠O的列向量是所给的齐次线性方程组之解，所以该齐次线性方程组有非零解，从而r（A）<3，即|A|=0（其中，A是所给齐次线性方程组的系数矩阵）.

由于 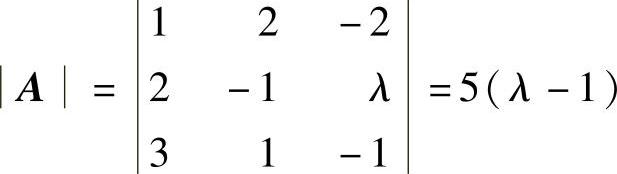，所以λ=1.

当λ=1时，，

即r（A）=2.因此所给方程组的基础解系中只包含一个解向量，从而B的列向量组线性相关，因此|B|=0.

例8.5 已知3阶矩阵A的第1行是（a，b，c），a，b，c不全为零，矩阵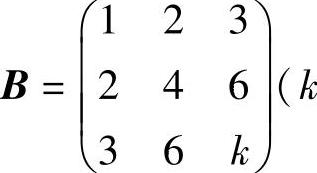为常数），且AB=O，求线性方程组Ax=0的通解.

精解 由AB=O知，B的每一个列向量都是Ax=0的解.

由AB=O得 r（A）+r（B）-3≤0，即r（A）+r（B）≤3.

（1）当k≠9时，r（B）=2，所以r（A）≤1，但A的第1行是非零行，所以r（A）≥1.从而r（A）=1.由此可知Ax=0的通解

x=C₁（1，2，3）^T+C₂（3，6，k）^T（C₁，C₂是任意常数）.

（2）当k=9时，r（B）=1，所以r（A）=2或1.

当r（A）=2时，通解为x=C（1，2，3）^T（C为任意常数）.

当r（A）=1时，

此时Ax=0与方程ax₁+bx₂+cx₃=0同解（其中x=（x₁，x₂，x₃）^T），设a≠0（当b或c不为零时也可同样考虑），因此此时的通解

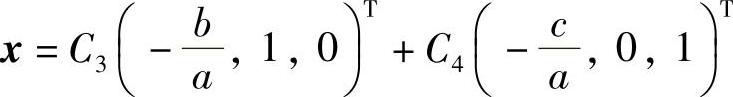（其中C₃，C₄是任意常数）.