零点定理、罗尔定理、拉格朗日中值定理与积分中值定理的综合应用

3.1零点定理

设函数f（x）在[a，b]上连续，且f（a）f（b）<0，则存在ξ∈（a，b），使得f（ξ）=0.

注 零点定理有各种推广形式，例如：

设函数f（x）在[a，b]上连续，且f（a）f（b）≤0，则存在ξ∈[a，b]，使得f（ξ）=0.

设函数f（x）在[a，+∞）上连续，且，则存在ξ∈（a，+∞），使得f（ξ）=0.

3.2罗尔定理

设函数f（x）在[a，b]上连续，在（a，b）内可导，且f（a）=f（b），则存在ξ∈（a，b），使得f′（ξ）=0.

注 罗尔定理有各种推广形式，例如：

设f（x）在[a，+∞）上连续，在（a，+∞）上可导，且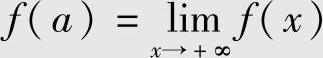，则存在ξ∈（a，+∞），使得f′（ξ）=0.

设f（x）在[a，b]上连续，在（a，b）内二阶可导，且对于a<c<b有f（a）=f（c）=f（b），则存在ξ∈（a，b），使得f″（ξ）=0.

3.3拉格朗日中值定理

设f（x）在[a，b]上连续，在（a，b）内可导，则存在ξ∈（a，b），使得

f（b）-f（a）=f′（ξ）（b-a）.

3.4积分中值定理

设f（x）在[a，b]上连续，则存在ξ∈[a，b]，使得

注 积分中值定理有以下的推广形式：

设f（x）在[a，b]上连续，g（x）在[a，b]上可积且不变号，则存在ξ∈[a，b]，使得

例3.1 已知函数f（x）在[0，1]上连续，在（0，1）内可导，且f（0）=0，f（1）=1，证明：

（1）存在ξ∈（0，1），使得f（ξ）=1-ξ；

（2）存在不同的两点η₁，η₂∈（0，1），使得f′（η₁）f′（η₂）=1.

精解 （1）记F（x）=f（x）-1+x，则F（x）在[0，1]上连续，且

F（0）F（1）=（-1）·1=-1<0，

所以，由零点定理知存在ξ∈（0，1），使得F（ξ）=0，即f（ξ）=1-_ξ.

（2）ξ将[0，1]划分成两个小区间[0，ξ]和[ξ，1]，且f（x）在这两个小区间上都满足拉格朗日中值定理条件，所以由拉格朗日中值定理知，存在η₁∈（0，ξ）和η₂∈（ξ，1），使得

所以，存在不同的两点η₁，η₂∈（0，1），使得

例3.2 设函数f（x）在[0，1]上连续，且f（0）=0及证明存在ξ∈（0，1），使得

精解 将欲证等式中的ξ改为x得

当x∈（0，1]时，上式可以改写成

，即

由此得故作辅助函数(www.xing528.com)

显然，F（x）在[0，1]上连续，在（0，1）内二阶可导，且F（1）=F（0）（=0）.所以由罗尔定理知，存在ξ∈（0，1），使得F′（ξ）=0，即

例3.3 设函数f（x）在[0，2]上连续，在（0，2）内二阶可导.证明下列问题：

（1）当f（x）满足f（0）=f（2）=0，f₊′（0）f-′（2）>0时，存在ξ∈（0，2），使得f″（ξ）=0.

（2）当f（x）满足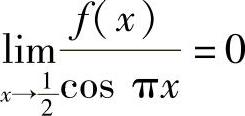和时，存在η∈（0，2），使得f″（η）=0.

精解 （1）由题设f₊′（0）f_-′（2）>0可设f₊′（0）>0，f_-′（2）>0（当f₊′（0）<0，f_-′（2）<0同样可证）.于是由左、右导数的定义得

由此可知，存在x₁，x₂∈（0，2）（x₁<x₂），使得

f（x₁）>f（0）=0，f（x₂）<f（2）=0.

于是由零点定理知，存在x₃∈（x₁，x₂）⊂（0，2），使得f（x₃）=0.

由此可知，f（x）在[0，2]上连续，在（0，2）内二阶可导，且f（0）=f（x₃）=f（2）（0<x₃<2），于是分别在[0，x₃]和[x₃，2]上应用罗尔定理知，存在ξ₁∈（0，x₃）和ξ₂∈（x₃，2），使得f′（ξ₁）=f′（ξ₂）=0.

由于f′（x）在[ξ₁，ξ₂]上满足罗尔定理条件，因此存在ξ∈（ξ₁，ξ₂）⊂（0，2），使得f″（ξ）=0.

（2）由题设得另外，由积分中值定理知，存在，使得由题设得f（x₁）=f（2）.于是，f（x）在[x₁，2]上满足罗尔定理条件，所以存在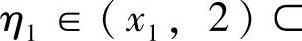，使得f′（η₁）=0.

由此可知，f′（x）在上连续，在内可导，且，所以由罗尔定理知，存在，使得f″（η）=0.

例3.4 设函数φ（x）具有二阶导数，且满足φ（2）>φ（1），，证明存在ξ∈（1，3），使得φ″（ξ）<0.

精解 由于φ（x）在[1，2]上可导，所以由拉格朗日中值定理知，存在ξ₁∈（1，2），使得φ（2）-φ（1）=φ′（ξ₁）（2-1）.由φ（2）>φ（1）得φ′（ξ₁）>0.

由积分中值定理知存在x₁∈[2，3]，使得于是由题设知φ（2）>φ（x₁）（由此可知2<x₁）.φ（x）在[2，x₁]上可导，由拉格朗日中值定理知存在ξ₂∈（2，x₁），使得

φ（x₁）-φ（2）=φ′（ξ₂）（x₁-2），

所以，由φ（2）>φ（x₁），2<x₁得φ′（ξ₂）<0.

在[ξ₁，ξ₂]上，φ′（x）可导，所以由拉格朗日中值定理知存在ξ∈（ξ₁，ξ₂）⊂（1，3），使得φ′（ξ₂）-φ′（ξ₁）=φ″（ξ）（ξ₂-ξ₁），即

例3.5 设函数f（x）在[a，b]上有连续的导数，且存在c∈（a，b），使得f′（c）=0.证明存在ξ∈（a，b），使得

精解 先将欲证等式中的ξ换成x得

显然这个以f（x）为未知函数的一阶线性微分方程的通解为

即，所以作辅助函数

显然F（x）在[a，b]上可导，且F（a）=0.当F（c）=0时，F（x）在[a，c]上满足罗尔定理条件，所以存在ξ∈（a，c）⊂（a，b），使得F′（ξ）=0.

下面证明在F（c）≠0时也存在使得F′（ξ）=0的ξ.

当F（c）≠0时，F（x）在[a，c]上满足拉格朗日中值定理条件，因此，存在ξ₁∈（a，c），使得

在[ξ₁，c]上，F′（x）连续，且

所以，由零点定理知，存在ξ∈（ξ₁，c）⊂（a，b），使得F′（ξ）=0.

综上所述，不论F（c）=0还是F（c）≠0，都存在ξ∈（a，b），使得F′（ξ）=0，即