一、选择题
(1)
分析 逐一判断各个选项中的反常积分的收敛性,直到得到收敛积分为止,如果前三个选项都不正确,则直接选(D)
精解 对于选项(A),由于
所以,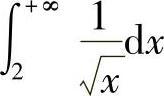 发散.
发散.
对于选项(B),由于
所以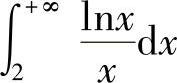 发散.
发散.
对于选项(C),由于
所以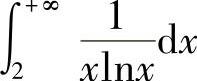 发散.
发散.
因此本题选(D).
附注 选项(D)确实是正确的,具体计算如下:
由于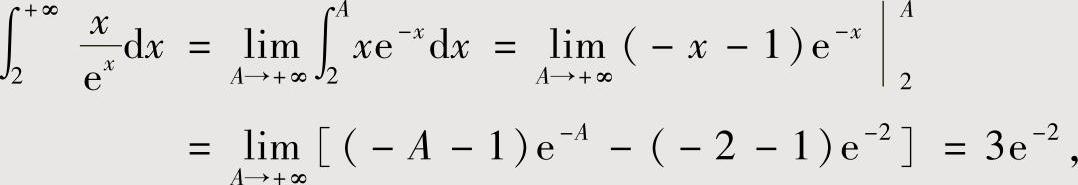
所以,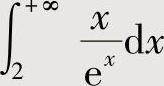 收敛.
收敛.
(2)
分析 先写出f(x)的表达式,确定有无间断点.如果有间断点,再确定其是可去的,跳跃的或是无穷的.
精解 当x=0时,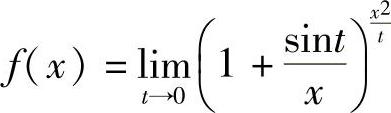 不存在,
不存在,
当x≠0时,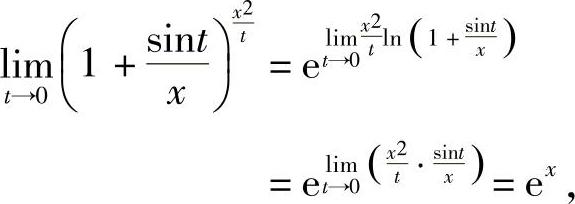
所以,f(x)有间断点x=0.
由于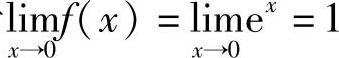 ,所以点x=0是可去间断点.
,所以点x=0是可去间断点.
因此本题选(B)
附注 x≠0时的f(x)表达式也可用以下方法计算:
(3)
分析 f′(x)在点x=0处连续时,f′(0)存在,且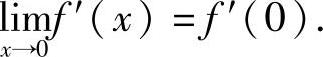 由此即可确定α,β应满足的关系式.
由此即可确定α,β应满足的关系式.
精解 要使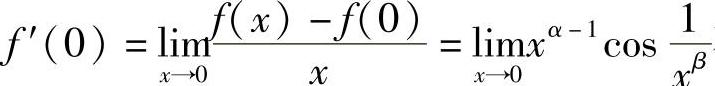 存在,必须有
存在,必须有
α-1>0.
要使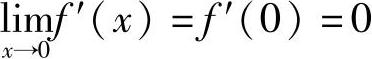 ,即
,即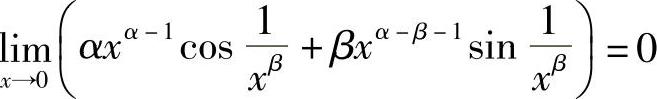 ,必须有
,必须有
α-β-1>0.
由此可知,当f′(x)在点x=0处连续,即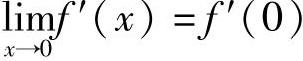 时,α,β必须满足
时,α,β必须满足
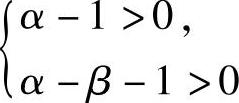 ,即α-β>1.
,即α-β>1.
因此本题选(A)
附注 题解中使用了以下结论:对于正数α,β,
要使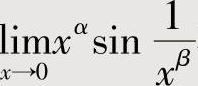 存在,或
存在,或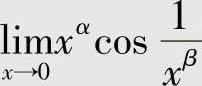 存在,必须α>0.
存在,必须α>0.
(4)
分析 从f″(x)的图像寻找f″(x)的零点与不存在的点入手.
精解 由于f(x)是连续函数,且从f″(x)的图像可知,f″(x)有两个零点,记为x1,x2,则x1<0<x2.此外,f″(0)不存在,所以曲线只有3个可能的拐点:(x1,f(x1)),(x2,f(x2)),(0,f(0)).
在点x=x1的两侧邻近,f″(x)不变号,所以(x1,f(x1))不是曲线y=f(x)的拐点.在点x=x2与点x=0的两侧邻近,f″(x)都变号,所以(x2,f(x2)),(0,f(0))都是曲线y=f(x)的拐点,即曲线y=f(x)有两个拐点.
因此本题选(C).
附注 设f(x)是连续函数,则曲线y=f(x)的拐点可按以下步骤寻找:
(1)计算f″(x)的零点与不存在点,设为x1,x2,…,xn.
(2)逐一判断,在各个点xi的两侧邻近,考察f″(x)是否变号.如果变号,则(xi,f(xi))是曲线y=f(x)的一个拐点;否则(xi,f(xi))不是拐点.
(5)
分析 由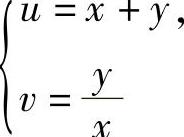 将所给方程改写成
将所给方程改写成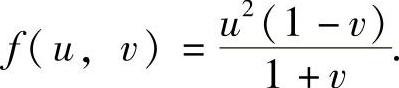 由此即可得到
由此即可得到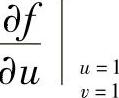 与
与
精解 由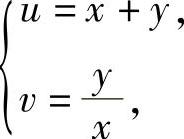 得
得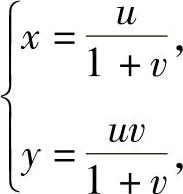 将它代入
将它代入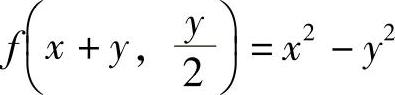 得
得
所以 
因此本题选(D).
附注 本题也可以按如下方法计算
由于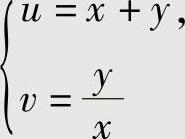 ,所以所给方程两边分别对x,对y求偏导数得
,所以所给方程两边分别对x,对y求偏导数得
将u=1,v=1,即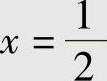 ,
,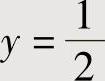 代入上式得
代入上式得
解此方程组得fu′(1,1)=0,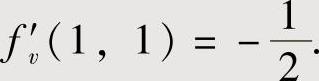
(6)
分析 画出D的图像,即可得到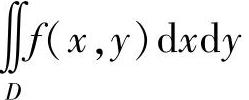 在极坐标系中的表示式.
在极坐标系中的表示式.
精解 D如图B-15-6的阴影部分所示,在极坐标系下
图 B-15-6
所以
因此本题选(B).
附注 当直角坐标系中的二重积分化为极坐标系中的二重积分时,应注意dxdy=rdrdθ,而不是dxdy=drdθ
(7)
分析 Ax=b有无穷多解的充分必要条件是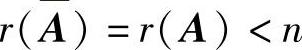 (其中
(其中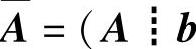 )是Ax=b的增广矩阵),由此即可得到正确选项.
)是Ax=b的增广矩阵),由此即可得到正确选项.
精解 对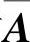 施行初等行变换:
施行初等行变换:
由此可知,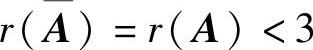 的充分必要条件是a为1或2,且d为1或2,即a∈Ω,d∈Ω.从而Ax=b有无穷多解的充分必要条件为a∈Ω,d∈Ω.
的充分必要条件是a为1或2,且d为1或2,即a∈Ω,d∈Ω.从而Ax=b有无穷多解的充分必要条件为a∈Ω,d∈Ω.
因此本题选择(D).
附注 应记住非齐次线性方程组有解、无解的判断方法:
设A是m×n矩阵,b是m维列向量,记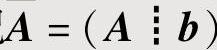 ,则线性方程组Ax=b有无穷多解的充分必要条件是
,则线性方程组Ax=b有无穷多解的充分必要条件是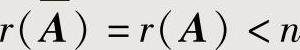 ;线性方程组Ax=b有唯一解的充分必要条件是
;线性方程组Ax=b有唯一解的充分必要条件是
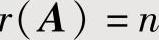 ;线性方程组Ax=b无解的充分必要条件是r(A)>r(A).
;线性方程组Ax=b无解的充分必要条件是r(A)>r(A).
(8)
分析 由题设可知,Ae1=2e1,Ae2=e2,Ae3=-e3.由此即可得到在正交变换x=Qy下,f(x1,x2,x3)的标准形.
精解 由题设知,
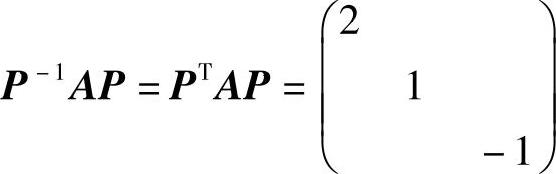 ,即
,即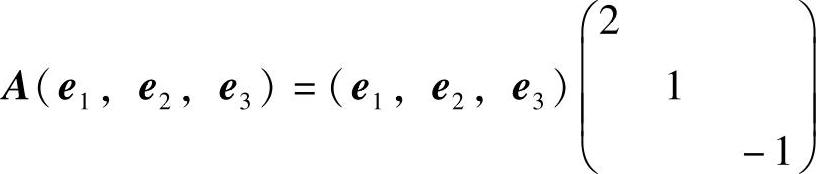 ,
,
所以有Ae1=2e1,Ae2=e2,Ae3=-e3.从而
Ae1=2e1,A(-e3)=-(-e3),Ae2=e2,
即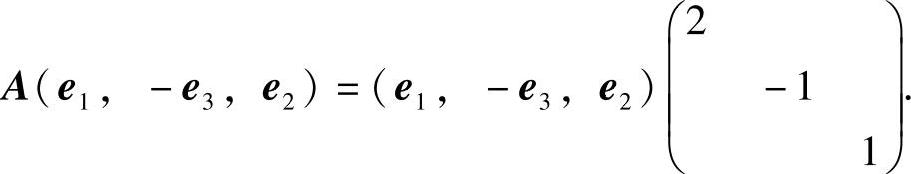 由此得到
由此得到
从而,在正交变换x=Qy下,f(x1,x2,x3)的标准形为2y21-y22+y23.
因此本题选(A).
附注 本题也可按以下方法计算:
由题设知,
并且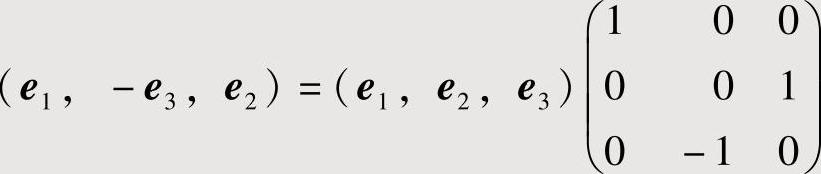 ,所以由式(1)得
,所以由式(1)得
从而在正交变换x=Qy下,f(x1,x2,x3)的标准形为2y21-y22+y23.
二、填空题
(9)
分析 先按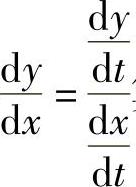 算出
算出 ,然后按
,然后按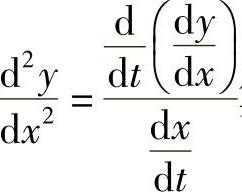 算出
算出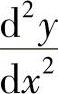 ,即可得到
,即可得到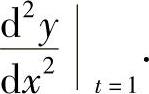
精解 由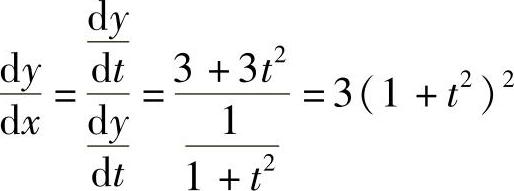 得
得
所以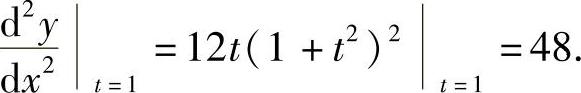
附注 本题的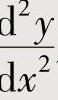 应按
应按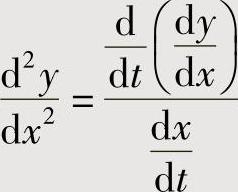 或
或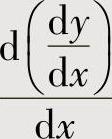 计算,而
计算,而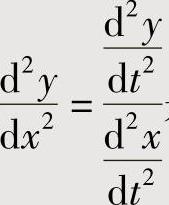 是错误的.
是错误的.
(10)
分析 分n=1及n>1两种情形计算.
精解 由f′(x)=2x·2x+x2·2xln2得f′(0)=0.
当n>1时,由
得f(n)(0)=n(n-1)(ln2)n-2.
附注 应先计算f′(0),然后利用公式
算出f(n)(x)(n>1),即得到f(n)(0)(n>1).
(11)
分析 将φ(x)写成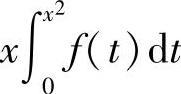 ,算φ′(x),然后由φ(1)及φ′(1)的值即可得到f(1).
,算φ′(x),然后由φ(1)及φ′(1)的值即可得到f(1).
精解 显然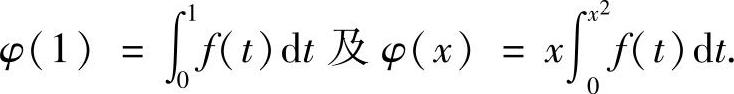 于是
于是
令x=1得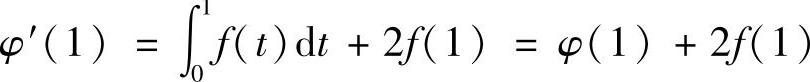 ,所以
,所以
附注 要计算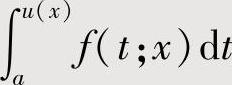 (其中,对于固定的x,f(t;x)是t的连续函数,u(x)可导)关于x的导数,应先将f(t;x)中的x移入积分上限(下限)或移到积分号外.
(其中,对于固定的x,f(t;x)是t的连续函数,u(x)可导)关于x的导数,应先将f(t;x)中的x移入积分上限(下限)或移到积分号外.
(12)
分析 先算出所给微分方程的通解,然后利用y(0)=3,y′(0)=0算出y(x).
精解 所给微分方程的特征方程
λ2+λ-2=0
有两个根λ=-2,1,所以通解为
y(x)=c1e-2x+c2ex, (1)
且 y′(x)=-2c1e-2x+c2ex. (2)
由于y(x)在点x=0处取极值3,所以有y(0)=3,y′(0)=0.将它们代入式(1)与式(2)得
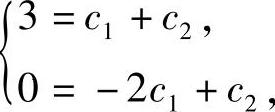 即c1=1,c2=2.
即c1=1,c2=2.
代入式(1)得y(x)=e-2x+2ex.
附注 顺便把题中的微分方程换成y″-2y′+y=0,其他条件不变,重新求解,具体如下:
由于y″-2y′+y=0的特征方程λ2-2λ+1=0有二重根λ=1,所以它的通解为
y(x)=(c1+c2x)ex, (3)
且 y′(x)=(c1+c2+c2x)ex. (4)
将y(0)=3,y′(0)=0代入式(3)与式(4)得
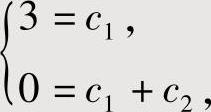 即c1=3,c2=-3.
即c1=3,c2=-3.
将它们代入式(3)得y(x)=3(1-x)ex.
(13)
分析 对所给方程两边求全微分,并将x=y=0代入即可算得dz|(0,0).
精解 所给方程两边求全微分得
ex+2y+3z(dx+2dy+3dz)+yzdx+xzdy+xydz=0,
即(1-xyz)(dx+2dy+3dz)+yzdx+xzdy+xydz=0.所以
[3(1-xyz)+xy]dz=(xyz-1)(dx+2dy)-yzdx-xzdy.
将x=y=0代入上式得
3dz|(0,0)=-dx-2dy,即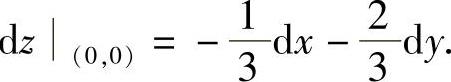
附注 本题也可以通过计算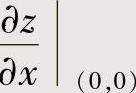 ,
,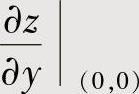 算出dz|(0,0),具体如下:
算出dz|(0,0),具体如下:
所给方程两边对x求偏导数得(https://www.xing528.com)
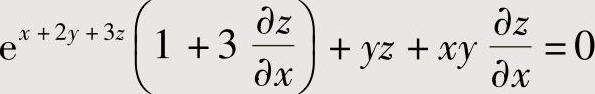 ,即
,即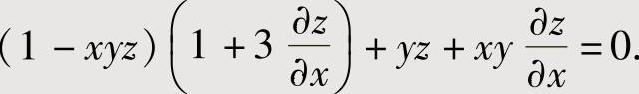
将x=y=0代入上式得
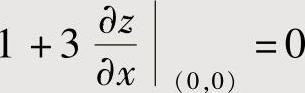 ,即
,即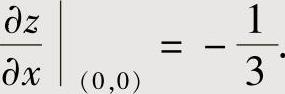
所给方程两边对y求偏导数得
将x=y=0代入得
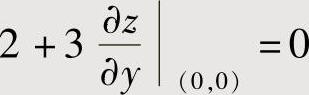 ,即
,即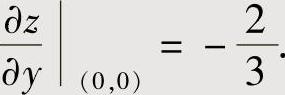
于是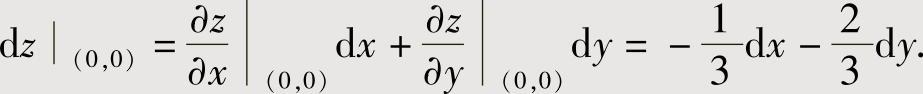
(14)
分析 算出B的所有特征值即可得到|B|.
精解 由于矩阵A有特征值为2,-2,1,所以矩阵B的所有特征值为
μ1=22-2+1=3,μ2=(-2)2-(-2)+1=7,μ3=12-1+1=1.
从而,|B|=μ1μ2μ3=3×7×1=21.
附注 设A是n阶矩阵,其有特征值λ及与λ对应的特征向量ξ;又设m次多项式f(x)=a0xm+a1xm-1+…+am-1x+am,则矩阵f(A)=a0Am+a1Am-1+…+am-1A+amEn有特征值f(λ)及与f(λ)对应的特征向量ξ.记住这一结论.
三、解答题
(15)
分析 写出f(x)的带佩亚诺型余项的3阶麦克劳林公式,即可由f(x)~g(x)(x→0),算出a,b,k的值.
精解 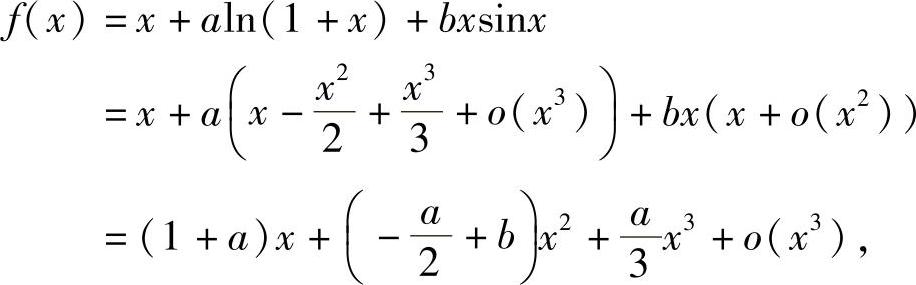
所以,由f(x)~g(x)=kx3(x→0)得
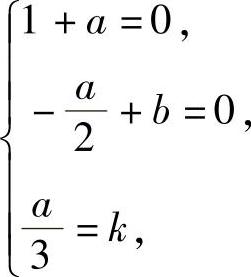 即a=-1,
即a=-1,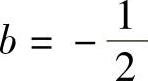 ,
,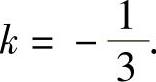
附注 本题也可用洛必达法则计算,具体如下:
由此得到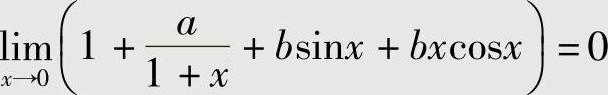 ,即a=-1.
,即a=-1.
将a=-1代入式(1)得
由此可得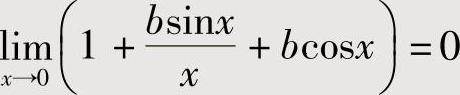 ,即
,即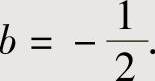
将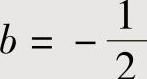 代入式(2)得
代入式(2)得
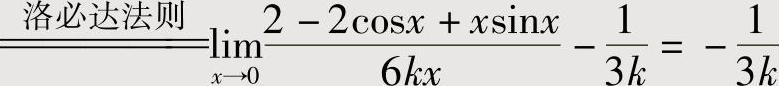 ,即
,即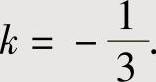
(16)分析 先算出V1与V2,然后令V1=V2即可算出A的值.
精解 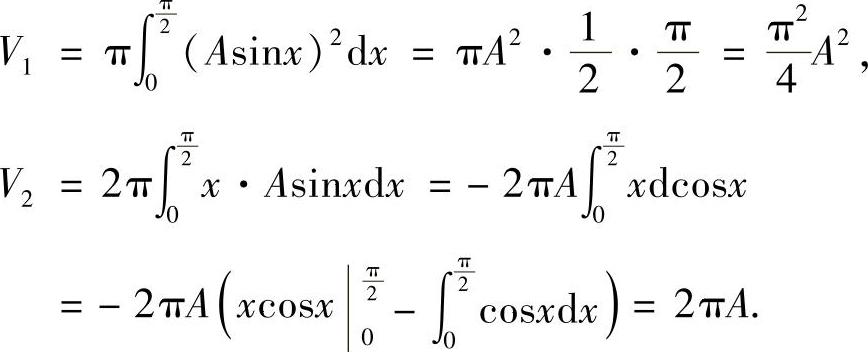
于是,由V1=V2得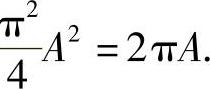 所以由A>0得
所以由A>0得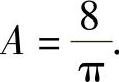
附注 设D是由直线x=a,x=b(a<b)及曲线y=f1(x),y=f2(x)(0≤f1(x)≤f2(x),a≤x≤b)围成,则D绕x轴旋转一周而成的旋转体体积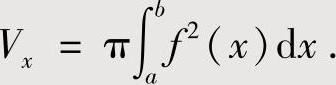
设D是由直线x=a,x=b(0<a<b)及曲线y=f1(x),y=f2(x)(0≤f1(x)≤f2(x),a≤x≤b)围成,则D绕y轴旋转一周而成的旋转体体积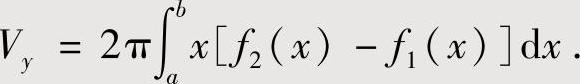
(17)分析 先由题设算出fx′(x,y),fy′(x,y)及f(x,y),然后按二元函数极值计算方法算出f(x,y)的极值.
精解 对f″xy(x,y)=2(y+1)ex关于y积分得
fx′(x,y)=(y+1)2ex+φ(x)(φ(x)是待定函数). (1)
将y=0代入式(1),并利用fx′(x,0)=(x+1)ex得φ(x)=xex.将它代入式(1)得
fx′(x,y)=(y+1)2ex+xex. (2)
对式(2)关于x积分得
f(x,y)=(y+1)2ex+(x+1)ex+ψ(y)(ψ(y)是待定函数). (3)
将x=0代入式(3),并利用f(0,y)=y2+2y得ψ(y)=-2.将它代入式(3)得
f(x,y)=(y+1)2ex+(x+1)ex-2,
于是,fy′(x,y)=2(y+1)ex.
由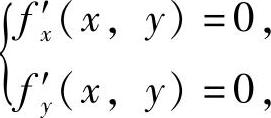 即
即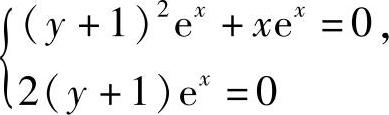 得唯一解x=0,y=-1.
得唯一解x=0,y=-1.
由于 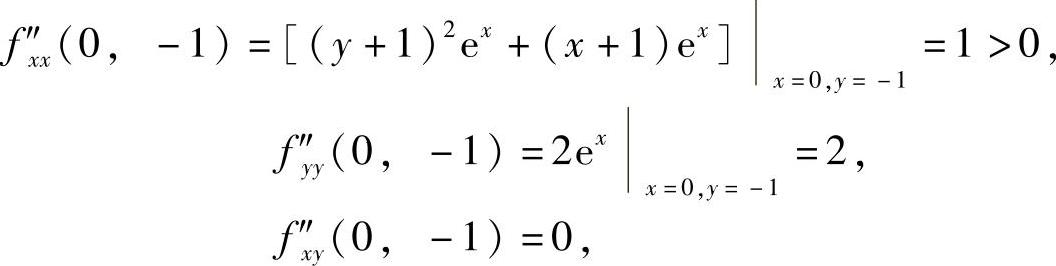
所以由Δ=f″xx(0,-1)·f″yy(0,-1)-f″xy(0,-1)=2>0知f(0,-1)=-1是f(x,y)的极小值,但f(x,y)无极大值.
附注 当f′(x)=φ(x)时有f(x)=Φ(x)+c(其中Φ(x)是φ(x)的一个原函数,c是任意常数);
当fx′(x,y)=φ(x,y)时,有f(x,y)=Φ(x,y)+c(y).(其中Φ(x,y)是y任意固定时φ(x,y)关于x的一个原函数,c(y)是y的任意函数).
图 B-15-18
(18)分析 画出D的简图,按照对称性化简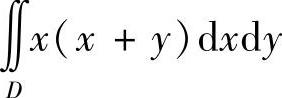 后计算.
后计算.
精解 D的图形如图B-15-18的阴影部分所示.
由于D关于y轴对称,在对称点处x2的值彼此相等,但xy的值互为相反数,所以
附注 在二重积分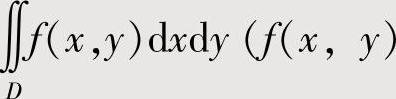 是二元连续函数)的具体计算之前,应做好两件事:
是二元连续函数)的具体计算之前,应做好两件事:
(1)画出D的概图;
(2)根据D的对称性,对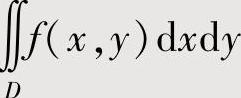 按以下公式化简:
按以下公式化简:
设D有某种对称性,则
其中,D1是D按其对称性划分成的两部分之一.
(19)分析 由f′(x)确定f(x)的单调区间,再由连续函数的零点定理,即可确定f(x)的零点个数.
精解 由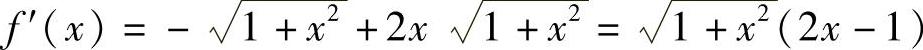 知,f′(x)有唯一零点
知,f′(x)有唯一零点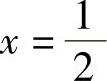 ,且
,且
当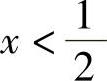 时,f′(x)<0,即f(x)在
时,f′(x)<0,即f(x)在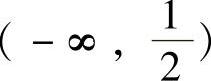 上单调递减,
上单调递减,
当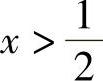 时,f′(x)>0,即f(x)在
时,f′(x)>0,即f(x)在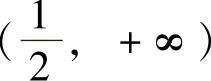 上单调递增.
上单调递增.
于是,由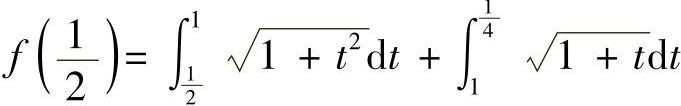
以及连续函数零点定理(推广形式)知f(x)在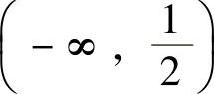 与
与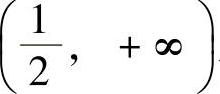 上各有唯一的零点.
上各有唯一的零点.
因此f(x)的零点个数为2.
附注 连续函数零点定理:
设f(x)在[a,b]上连续,且f(a)f(b)<0,则f(x)在[a,b]上至少有一个零点.这里a=-∞,或b=+∞也成立(推广形式).
设f(x)在[a,b]上连续且单调,则当f(a)f(b)<0时,f(x)在[a,b]上有唯一的零点.这里a=-∞,或b=+∞也成立(推广形式).
(20)
分析 由题设列出关于物体在t时刻温度T(t)的微分方程,并求解该微分方程,即可得到使物体温度从30℃降到21℃所需的时间.
精解 由题设得
由式(1)得T(t)-20=cekt. (4)
将式(2)代入式(4)得c=100.于是式(4)成为
T(t)=20+100ekt. (5)
将式(3)代入式(5)得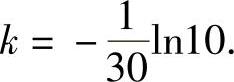 将它代入式(5)得
将它代入式(5)得
于是,当T(t)=21时,由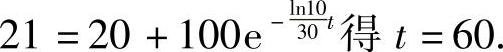 即物体从30℃降到21℃所需的时间为60-30=30min.
即物体从30℃降到21℃所需的时间为60-30=30min.
附注 由于微分方程的通解中含有两个未知常数k与c,故先应利用T(0)=120,T(30)=30确定这两个常数,从而确定T(t).
(21)
分析 先算出x0,然后证明x0<b及x0>a.
精解 曲线y=f(x)在点(b,f(b))处的切线方程为
y-f(b)=f′(b)(x-b),
于是,它与x轴的交点横坐标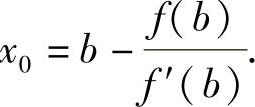
由f′(x)>0及f(a)=0知f(b)>f(a)=0,从而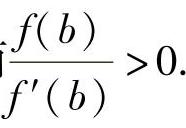 因此x0<b.
因此x0<b.
下面证明:x0>a.
由于f(x)在[a,b]上满足拉格朗日中值定理条件,所以存在ξ∈(a,b),使得
(b-a)f′(ξ)=f(b)-f(a)=f(b). (1)
于是由f″(x)>0知f′(b)>f′(ξ),所以由式(1)得
(b-a)f′(b)>f(b),从而有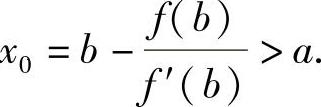
附注 实际上x0>a可从曲线y=f(x)的凹凸性直接得到.
由于f″(x)>0,所以曲线y=f(x)在[a,b]上是凹的,因此曲线y=f(x)在点(b,f(b))的切线必位于该曲线的下方,从而切线与x轴交点必位于曲线与x轴交点的右侧,即x0>a.
(22)
分析 (Ⅰ)由A3=O得|A|=0.由此可得a的值.
(Ⅱ)所给的矩阵方程可以改写成
(E-A)X(E-A2)=E.
由此可以算出X.
精解 (Ⅰ)由A3=O得|A3|=0,所以|A|=0. (1)
另一方面
由式(1),式(2)得a=0.
(Ⅱ)由所给的矩阵方程得
X(E-A2)-AX(E-A2)=E,即(E-A)X(E-A2)=E. (3)
由此可知,E-A,E-A2都可逆.
将a=0代入A得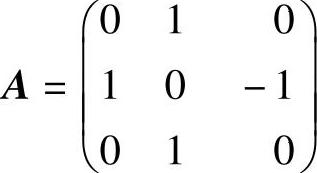 ,所以
,所以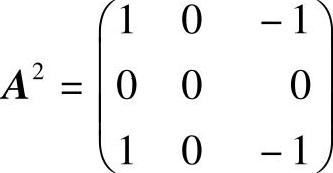 ,且
,且
于是,由式(3)得
附注 对于矩阵方程AXB=C(其中,A,B,C都是n阶已知矩阵),可按以下方法求解:
(1)如果A,B都是可逆矩阵,则X=A-1CB-1.
(2)如果A,B中只有一个可逆,例如A可逆,则XB=A-1C,然后将X=(xij),B=(bij), 代入转化成线性方程组算出xij(i,j=1,2,…,n),即得X.
代入转化成线性方程组算出xij(i,j=1,2,…,n),即得X.
(3)如果A,B都不可逆,则将X=(xij),A=(aij),B=(bij),C=(cij)代入AXB=C转化成线性方程组,算出xij(i,j=1,2,…,n),即得X.
(23)
分析 (Ⅰ)利用A~B及相似矩阵性质算出a,b之值.
(Ⅱ)将(Ⅰ)算出的a值代入A,将A相似对角化,即可得到可逆矩阵P.
精解 (Ⅰ)由A~B知,
解此方程组得a=4,b=5.
(Ⅱ)将a=4代入A得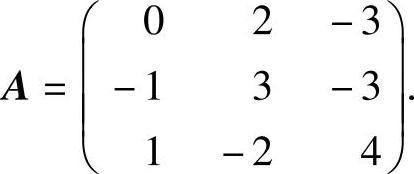 由于
由于
所以,A有特征值λ=5,1(二重).
设A的对应λ=5的特征向量为α=(a1,a2,a3)T,则α满足
它有基础解系(-1,-1,1)T,故可取α=(-1,-1,1)T.
设A的对应λ=1的特征向量为β=(b1,b2,b3)T,则β满足
它有基础解系(2,1,0)T,(-3,0,1)T,故可取β=β1=(2,1,0)T,β=β2=(-3,0,1)T.
于是,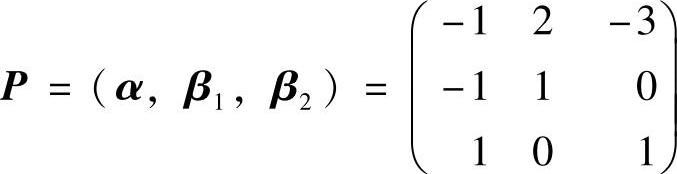 即为所求的可逆矩阵,它使得
即为所求的可逆矩阵,它使得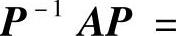
附注 设A,B都是n阶矩阵,则
(1)当A~B时,A,B有相同的特征多项式,特别有
trA=trB,|A|=|B|.
(2)当A~B时,如果A可逆,则B可逆,且A-1~B-1,A∗~B∗.
(3)设A~B,即存在n阶可逆矩阵P,使得P-1AP=B,则当A有特征值λ及其对应的特征向量ξ时,B有特征值λ及其对应的特征向量P-1ξ.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




