多重分形谱：数字建筑与增强打印技术的重要成果

从图4-10上可以看出，随着层次的不断加深，区间变得越来越碎，而质量在这些小区间上的分布就会越来越参差不齐（奇异性Singularity），但是对于每一个给定的层，所有小区间上的质量之和都为1，这是因为在不断加深层次的时候，质量在小区间上的分配都满足守恒律。可以用一个被称作多重分形谱的曲线来刻画这种奇异性。

首先，在第t步的时候，任意一个小区间i的质量可以写成：

其中p就表示在每一次划分的时候，分配到左边小区间的质量比率。例如，在上述例子中，每次1/3的质量划分给左侧区间的话，那么p=1/3。x表示的是该小区间i在t步生成过程中共有多少次被分配到了左侧，这样t-x对应的就是分配在右侧区间的次数。如图4-11所示，红色的线条就表示分到了左侧，绿色线条分配在右侧。

图4-11　多重分形谱的曲线

因此，在T=5这个层次的小区间中，质量为的区间可能不止一个，只要从T=1到T=5的任意一条路径中包含x个向左的分支，t-x个右分支，最终的质量就都一样。事实上，我们可以计算出来具有质量的小区间总共有个。这样，对于层次t来说，得到两个量：

是小区间的质量，另一个是质量为m的小区间个数，记为：

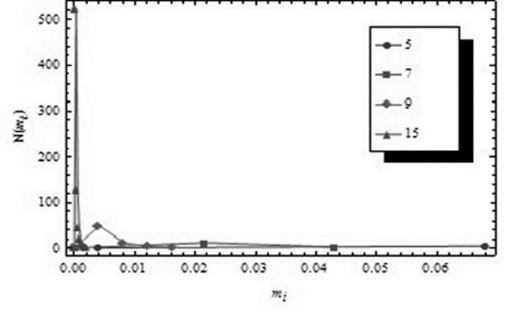
通过将上述两个等式中的x消去，不难找到N和mi之间的函数关系，这个函数关系刻画了第t层小区间质量的分布情况。如图4-12所示，画出不同t对应的N（mi）曲线（不同的曲线对应不同的t）：

(www.xing528.com)

图4-12　第t层小区间质量的分布情况

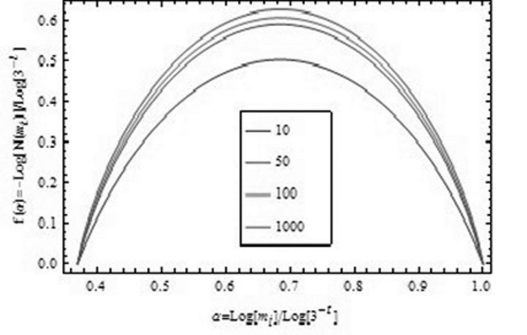
图4-13　康托尔集合上质量分布的多重分形谱

当t逐渐变大的时候，这条曲线会变得越来越尖，表示有很多小区间具有相同的质量值，而大部分区间质量参差不齐。这种图像不方便比较，需要想办法把这个尖抹平。一种简单易行的方法就是取对数坐标。然而，对数坐标的底取多少合适呢？可以设这个底为一个常数e，但是，考虑到无论N还是mi以及小区间的大小都会随着t而呈现指数类型的增长或者衰减。因此，可以考虑对数底定为t层次每个小区间的长度大小，即3-t。这样一来，便可以得到很规整的图4-13。

在 图4-13中，画 出 了 不 同t所 对 应 的对的曲线（取负号是因为该数值可以被解释为分形维）。随着t逐渐的增大，曲线不仅没有出现高高的尖峰，而且逐渐趋近于一条光滑的闭合曲线。这是因为，随着t的增长，对数之底也会快速地衰减，从而使得这条曲线会逐渐稳定。那么，当t趋于无穷大的时候，这条曲线就构成了康托尔集合上质量分布的多重分形谱。

实质上，上述做法不仅可以让质量在各个小区间上的分布图形更加好看，它还具有更深刻的含义。分形研究的是当观察精度不断提高，被观察的几何形体是如何变化的。那么，当计算log（mi）随着log（3-t）而变化的时候，实质上是在计算质量如何随着观察分辨率的提高而衰减。更一般地，不妨把这个质量随观察精度而变化的速度定义为一个量：

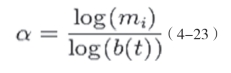
假设把一个集合划分成不同精度t的盒子，那么每个盒子的大小就是b（t）。在康托尔集合的例子中，这个盒子就是一维线段上的小区间，直线段的长度就是盒子尺寸b（t），也就是3-t。这样，每个小盒子都能计算出一个α值，那么当给定了一个α以后，能够数出来一共有多少个小盒子与之对应。这个数等价于前面讨论的N，只不过，在这里计算的不是具有相同的质量mi的小盒子的个数，而是具有相同的α，即质量随精度变化速度相同的小盒子个数。当t给定的时候，这两种描述实际上是等价的。于是，定义多重分形谱为：

其中N（α）就表示质量变化速度位于区间[α，α+dα]之中的小区间个数。如果以前接触过分形，以及计算分形维中的盒计数法的话，就会发现，实际上这个f（α）就是分形集合：“所有那些具有相同α的小盒子的集合”的分形维。

于是，图景一下子就清楚了，实际上所谓的多重分形谱，就是描述一个崎岖地形的数学工具。其中，地形的高度就对应着质量的分布，质量越多的地方，高度越高。这种地形很怪异，因为它会随着观察尺度越来越精细而越来越坑洼不平。如果采用不同的盒子来划分水平面，从而把一个盒子中的山脉地形中的所有高度加总形成了粗粒化的新的高度，那么随着盒子越来越小，这种粗粒化的地形就会越来越颠簸。以上的描述手段就相当于：在一个观察精度下，用不同的水平面去截取这个地形，形成一些等高线，那么等高线所包围的区域就构成了一个分形，于是可以计算出它的分形维度。这样，该分形维如何随着α，即等高线高度对数与观测尺度对数的比值，而变化就够成了多重分形谱。那么，这个多重分形谱的不同形状也就有了一定的解释。首先，如果这个地形是一个扁平的地形，也就是所有地点的高度都相同，那么多重分形谱就退化为一个点，这个点的横坐标是1，纵坐标是这个地形的支撑集合（即地形在XOY平面上的投影）的分形维。当地形稍微崎岖一点的时候，这个多重分形谱曲线就会具有一定的宽度。宽度越宽表示地形高度的取值越多样化。而多重分形谱曲线上的高度则对应了不同等高线所围分形集的维度，维度越大则表示分形集合的复杂程度越高，也就表示地形褶皱会比较多。