（1）平衡态的流网络
对于平衡流动来说，总可以将整个流系统看作一个多粒子沿着网络流动的系统。例如，对于图4-7所示网络，当某个处于1号节点的粒子往外流动的时候，它可能会跳到2号节点，也可能会跳到3号节点。可以想到，由于1到2号节点的流量比到3号的节点大，所以这个粒子更有可能跳到2号节点。不妨假设粒子跳转到某个节点的概率是与这条边上的流量成正比的。也就是说，因此，粒子会以5/8=50/80的概率从1跳到2，而以3/8=30/80的概率从1到3。同样的道理，当粒子跳入到任何一个节点后，它都会沿着边以概率跳转。
因此，整个平衡态的流网络可以看作一个马尔可夫链，其中每个节点相当于是粒子所处的可能状态，节点之间的跳转可以看作概率转移。具体的，对于任何的处于平衡的流网络F，定义矩阵M为概率转移矩阵，其中M中的第i行第j列的元素就是粒子处于i状态下转移到j状态的概率，记为：
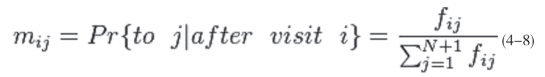
当粒子进入汇节点N+1，它就不会再往外跳了，因此，状态N+1就相当于马尔可夫链的吸收态。注意，根据矩阵M的定义，它自然满足概率归一化条件：
另外一个比较有趣的事实是，根据流矩阵F，还可以定义另外一个马尔科夫链M'，称为逆向马尔科夫链。它刻画的是一个逆向的因果过程，也就是说如果2号节点观察到了一个新到的粒子，那么它有可能从1号节点过来也可能从3号节点过来。显然1到2的流量要比3到2的流量大得多，因此粒子从1跳过来的可能性会更大。那么，既然整个网络是平稳的，不难想到，在2号节点观测到一个粒子的条件下，它是从1号节点跳过来的概率是5/6=50/60，它从3号节点跳过来的概率是1/6=10/60。
更一般地，定义逆向马尔科夫链M'，其中任意的元素m'ij定义为：观察到粒子来到了节点i的条件下，它可能是从j节点流过来的概率。它按照下式计算：
同样地道理，它也是归一化的，即：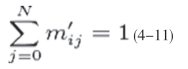
(www.xing528.com)
这个逆向马尔可夫链又可以看作逆向流矩阵FT（即原始流矩阵F的转置）所对应的正向马尔科夫矩阵，这是因为：
其中逆向流矩阵就相当于把原始流网络所有的有向边都掉转方向，并保持所有的流量不变。由于网络是平衡的，所以逆向的流网络必然也是平衡的。这似乎描绘了一个有趣的图景：在一个平衡的流网络中，所有的粒子都顺着流动从源到汇。而与此同时，如果从汇观察到粒子，并不断地询问这个粒子是从哪个节点跳转过来的，就得到一个反向的信息流动，仿佛是有假想的粒子从汇流到了源一样。
（2）投入产出分析
在经济系统中存在着大量的流动：货币流以及物品流。经济学家（wikipedia：Wassily Leontief）很早就开始对流动展开了研究，只不过他们采用了非常不同的技术，这种技术就是投入产出分析（Input-output analysis）。投入产出分析是基于一种投入产出表，所谓的投入产出表就是类似下面的形式：
其中，1，2，3，...，N表示工业系统中的N个部门（Sector），例如农业、林业、造纸业等等。zij表示从i部门对j部门的投入量（一般以货币来衡量）。例如，如果i表示林业，j表示造纸业，zij=350000，则表示造纸业从林业部门购买了350000人民币的原始木材。倒数第二列fi则表示第i部门到最终需求（即消费者的最终消费）的直接流量（以货币衡量）。例如，如果fj=500000，就表示人们对纸张的最终需求有500000元。最后一列xi表示行业i的总产出。投入产出表要求：
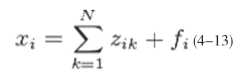
它表示第i部门的总产出应该等于其他所有工业部门对i部门的需求再加上最终消费者对i的直接需求。虽然投入产出表与流量矩阵非常相似，而上式又几乎可以看作流量平衡条件，但是，投入产出表和流网络模型还有细微的差别。必须经过特定的转换才能将投入产出表与流量网完全等价。其次，投入产出分析也与基于马尔科夫链的流网络分析方法本质相同。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
