数字建筑与增强打印技术：CA思想及组成

1.CA基本思想

CA即CellularAutomata，称作单元自动机，它就是一种模型，可以让大量的简单单元在某些简单的本地规则作用下产生各种复杂的系统状态。这种模型的结构很简单，它是由很多的格子集合在一起所组成的，而每个格子就好像一个容器。而这个容器没有别的用处，只是作为一个代表，它告诉我们，在容器所在的那个位置上有没有放东西或放了多少。模型的实现主要依靠一些简单的规则。这些规则每次作用时都是只对几个相邻的容器起作用，所以称它为本地规则。这些规则的作用是规定每个容器里面放不放东西，这是由它周围相邻的容器是不是放了东西所决定的，比如说，往一些容器里放东西时，为了某种原因，如美观性，往往先看一看，某个容器的相邻的容器是不是放了东西，如果放满，就决定在那个空的容器里放东西。

通常，单元自动机是一套格子的n维组合，n为自然数，每个格子驻留了一个有限状态自动机，每个自动机以其相邻的，具有有限状态的单元格的状态作为输入，然后输出一个处于同一有限状态集合的状态。元胞自动机的状态是与其相邻的自动机状 态交互作用的结果。元胞自动机的相邻单元取舍情况一般如图4-1所示：

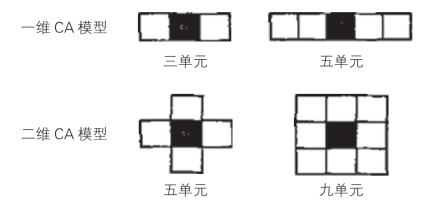
图4-1　CA模型

以上模型均将中央单元作为邻居，实际上，也可以不包括中央单元。CA 模型是建立在一个简单状态集和一套本地交互规则基础上的，是可以自我发展、自我完善的、可以不断扩展并可以按一定规则描述复杂系统状态和预测系统未来的自动机器。事实上，这个模型是一个二维CA模型，在CA思想的应用中还可以建立一维，二维和多维CA模型。它们都是按照这样一个简单的方法建立起来的 以模拟和仿真大型复杂的静态，动态和混合形式的系统。从算术的关系角度来看CA模型实际上是从有限状态机（Finite State Machine）演变而来的，但是CA 模型在更高层次上处理一维、二维或多维复杂系统的状态演化。它主要处理单元阵列上单元状态的读、写和更新的过程。

（2）CA的组成

①元胞，又可称为单元，或基元，是元胞自动机的最基本的组成部分，元胞分布在离散的一维、二维或多维空间上。

②状态，状态可以是{0，1}的二进制形式，也可以是整数形式的离散集。严格意义上，元胞自动机的元胞只能有一个状态变量，但在实际应用中，往往将其进行扩展。

③元胞空间，元胞所分布在空间网点的集合。对于它的几何划分，理论上，它可以是任意维数的欧几里德空间规则划分，目前研究多集中在一维和二维的元胞自动机上，对于一维元胞自动机，元胞空间的划分只有一种，而高维的元胞自动机，元胞空间的划分就可以有多种形式，对于最常见的二维元胞自动机，二维元胞空间通常可以按照三角、四方或六边形三种网格排列，如图4-2所示：

图4-2　元胞空间的常用划分方式

这三种规则的元胞空间划分在建模的时候各有优缺点：

三角网格的优点是有相对较少的邻居数目，这在某些时候很有用，可以大大减少运算量，其缺点是在计算机的表达与显示上不太方便，需要转换维四方网格；四方网格的优点是简单而且直观，而且特别适用于计算机环境下进行表达显示。其缺点是不能较好的模拟各向同性的现象；六边形网格的优点是可以较好的模拟各向同性的现象，因此模型更加自然和真实，其缺点和三角网格一样，不利于表达显示。

对于边界的处理，实际上，在模拟指定的元胞自动机演化规则的时候，不可能处理无限的网格，系统都是有限的、有边界的。显然，属于网格边界的格位 具有与其他内部网格一样的邻居。为了确定这些边界网格的行为，可以指定不同的演化规则，以考虑适当的邻居。即对边界上格位的信息进行编码，并根据这些信息选择不同的演化规则。按照这种方法，还可以定义几种完全不同行为的边界。

另外一种方法是，不是在系统边界上使用不同的演化规则，而是在边界处扩展格位邻居。例如，一种通用的解决办法是在假设周期或循环的边界条件，就是假想网格嵌入像环面一样的拓扑结构中。在二维网格条件下，指左右联结和上下联结。图4-3中给出一维网格中几种可能的边界条件。假定用边界外的一组虚元胞扩大网格，固定边界是用预先复制的元胞使邻居完整，通过对虚元胞赋予格位值，获得绝热的边界，映射边界相当于在虚元胞中复制其他邻居的值。

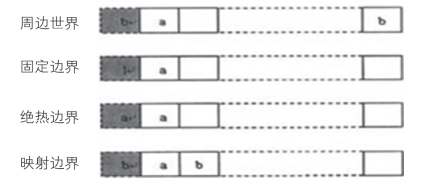
图4-3　各种边界条件

④邻居，按照定义，元胞自动机的演化规则是局部的，对于指定的元胞的状态进行更新只需要知道其邻居元胞的状态，某元胞需在其内搜索的空间叫作邻居，原则上，对于邻居的大小没有限制，只是所有的元胞的邻居的大小都要相同。实际上往往只由相邻的元胞构成邻居。

通常，二维元胞自动机考虑两种邻居：一是Von Neumann邻居，由一个中心元胞（要演化的元胞）和与其相邻接的东、西、南、北四个方位的四个元胞组成；另一是Moore邻居，他由一个中心元胞和与其相邻接的东、西、南， 北，以及东北、西北、东南、西南共9个元胞。两种标准邻居如图4-4所示：(www.xing528.com)

图4-4　两种标准邻居：a）Von Neumann 邻居 b）Moore 邻居

⑤规则，根据元胞当前状态以及邻居状态确定下一时刻该元胞状态的动力学函数，简单讲，就是一个状态转移函数。

⑥时间，元胞自动机是一个动态系统，它在时间维上的变化是离散的，即时间t是一个整数值，而且连续等间距。一般来说，一个元胞在t+1时刻的状态只决定于t时刻该元胞状态及其邻居元胞的状态，显然，在t-1时刻的该元胞及其邻居元胞状态间接（时间上延迟）影响了元胞在t+1时刻的状态。

（4）CA边界问题分析

通常元胞自动机边界问题的处理方法基于两个不同思想：认为所有系统处于一个封闭的环境中，在系统内部所有单元等同，所以无须考虑边界问题，但此系统是有限系统；认为边界问题可以容入系统内部处理，只是在处理这些事实上的边界的时候，按照等同与系统内部的单元来处理时，增加附加条件。

对于前者，通常采用以下处理方法：将系统的边界联结起来：如图4-5 所示：

图4-5　—维CA模型边界问题

上图是在处理一维CA模型边界问题时，采用的方法是将两个边界单元联结起来，这样，系统就相当于一个封闭系统，所有单元都可以按一个进化规则来处理，二维的依次类推，如图4-6所示：

图4-6　二维CA模型边界问题

二维边界处理时，可以将上边界单元和下边界单元联结起来，左边界单元和下边界单元相联结对角顶点相联结，

对于后者，解决方法是将系统边界的外围，人为的加上一个附加边界，这个附加边界的出现将使以前的边界单元成为系统内部单元，这样，这些单元就可以和其他的单元采用相同的规则处理，从而，达到系统进化的一致性。当然 附加的边界单元实质上是不参与系统进化的。

在上面的解决方法是在系统的外围人为的加上一个附加单元层，从而使实 际进化系统单元达到统一，避免处理上的各种困难。但是以下问题是需要解决的，否则无法用这些方法。

①确定附加单元的分布，由于单元的分布情况不同，则系统进化过程中，附加单元对实际进化单元的作用就将不同。所以这个问题处理的质量将直 接影响系统的最终结果。

②按照系统需求拟订附加单元的状态，由于附加单元的状态在进化过程中将影响实际进化单元，同时又由于，附加单元的状态在整个进化过程中保持不变，所以它们的状态一定要符合系统进化初始条件的要求，比如，初始化时，各个单元的状态是否对将来的系统进化结果的影响可以忽略。

③附加单元状态和系统进化的关系处理，这个问题主要存在于那些系统状态可以按不同形式处理的时候，比如，有时为了便于计算机处理而将二维 CA系统的进化过程可以转化为一维CA系统来进化，这时附加边界单元的状态和实际进化单元的关系将要随着系统的形式不同而不同。