用X射线应力分析仪测量残余应力的检测原理基于晶体的X射线衍射理论。当一束具有一定波长λ的X射线照射到多晶体上时，如图2-16所示，会在一定角度2θ上接收到反射的X射线强度极大值（即衍射峰），这便是X射线衍射现象。X射线的波长λ、衍射晶面间距d和衍射角2θ之间遵从著名的布拉格定律：
图2-16 X射线衍射原理［74］
布拉格方程反映了晶面间距和衍射角的关系，它的微分形式则表明了衍射角变化和材料应变的关系，见下式：
根据经典弹性力学理论，各向同性材料在任意方向上的应变可以由三个方向上的应力表示，其关系式如下式所示（式中，Ψ为测试角，Φ为所要测得应力的方向）［75-76］：
因此材料受力状态可以被当作平面应力状态，在平面状态下有
综合式（2-74）～式（2-76），简化后可以得到式（2-77），该式反映了各向同性材料自由表面Φ方向上的应力RΦ、测试角Ψ及衍射角变化（θ－θ0）三者之间的关系。将等式（2-75）的每一项都对sin2Ψ做偏导，就可以得到式（2-77）。式（2-77）就是传统一维线探方法采用的残余应力测试分析方法，通过改变测试角Ψ，测得不同测试角下衍射角的变化，最终通过对测试数据的拟合可以得到Φ方向上的残余应力RΦ：
2）基于X射线二维面探的残余应力测试原理
X射线二维面探残余应力测试方法在机理上和传统线探方法一致，都是通过衍射角和应变之间的布拉格方程关系来计算残余应力。两者的区别在于一维线探需要改变测试角来进行多次测量；二维面探只需要在测试角Ψ0下单次曝光，测试一个二维面上的衍射角变化，就能计算出测试方向Φ0上的残余应力。图2-17a显示了二维探测面下的完整德拜环，其光路图如图2-17b所示，其中η表示衍射角的补角，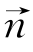
表示产生衍射的衍射面的法线方向。(www.xing528.com)
图2-17 二维面探X射线衍射残余应力测试光路图［77］
布拉格方程反映晶面间距和衍射角的关系，它的微分形式则表明了衍射角变化和材料应变的关系，如式（2-79）所示：
在确定了测试角ψ0后，就可以通过向量加法得到在测试面Ψ0上所有发生衍射的衍射面方向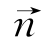
（n1，n2，n3）［7879］，其中
对于测试面上不同的α方向，都有其对应的衍射面，各个衍射面上的衍射角变化，对应于这些面上的应变。由弹性力学应变张量计算法则，不同方向上的应变可以由三个方向上的应变表示［80 81］：
平面应力下有γyz＝γxz＝0，将式（2-80）代入式（2-81）后得
定义α1和α2如式（2-82）所示，将式（2-81）代入式（2-82）后，就可以得到X射线二维面探采用的残余应力分析方法，如式（2-83）所示：
二维面探仪有500个探测头，均匀分布在一个360°面上，通过每一个探测器测得的衍射角变化，就能得到500个方向上的应变值，代入式（2-82）后，就可以计算出125个a1，将a1对cosα做偏导，就可以计算出材料的残余应力：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
