从《残余应力基础理论及应用》中获得的实际成果

Bolshakov等［11］在1996年通过实验和有限元模拟发现，8090铝合金的硬度不受残余应力的影响，也就是说材料的硬度不随残余应力的改变而改变。基于硬度不变的前提，Suresh［12］在1998年提出了一种测量等双轴残余应力的理论模型；Yun-Hee Lee等［13-15］也于2002年、2003年和2004年先后提出了三种测量残余应力的模型，其中前两种模型讨论的是等双轴残余应力，后一种测试扩展到了非等双轴平面应力。

2.1.2.1　Suresh理论模型［12］

由于平均接触应力Rave（等效于硬度H）不受任何固有应力的影响，因而有

式中，F、A分别为存在残余应力时的载荷和压痕面积；F0、A0分别为无残余应力时的载荷和压痕面积。

根据Kick定律，载荷-位移曲线可表示为

式中，C0、C分别为无残余应力和有残余应力时载荷-位移曲线的加载曲率；h0、h分别为无残余应力和有残余应力时的压入深度。

压痕面积A0和A可以表示为

式中，D0、D为压痕面积的度量，这两个参数与压痕接触周边的堆积和凹陷效应有关。

由式（2-11）～式（2-13）可得

同理

1）残余拉应力

上述模型针对的是等双轴残余应力，即，可以等效为静水应力，加上一个单轴压应力。

残余拉应力从x释放到y时，压入载荷增大，则

在有残余应力的材料上压入载荷F1，记为x。压痕状态从x到z变化，要经过两个步骤：

（1）载荷由F1降到F2，F2＝F1－RhA1，载荷从x到y；

（2）固定载荷F2，压痕深度从h1降到h2：

由式（2-22）和式（2-23）得

即

2）残余压应力

与拉应力的情况相似，同理可得固定压痕深度时残余应力的计算公式为

固定载荷时残余应力的计算公式为

式中，α为压头边界与材料表面的夹角。在此情况下引入sinα是因为：与拉应力不同，压应力的存在促使压头与样品接触，因而不能直接改变拉应力公式中残余应力的符号来得到压应力的公式。

2.1.2.2　Lee理论模型Ⅰ［13］

2002年，Yun-Hee Lee等提出了一种用压痕法测量DLC/Si和Au/Si薄膜残余应力的方法，它针对的是等双轴残余应力。该方法的前提是假设硬度不变，但加载曲线斜率改变。当固定压痕深度时，为了满足硬度不变的前提，材料被压表面形貌必然会发生变化。压头压入时的表面形貌如图2-4所示。当残余应力从拉应力释放到零再到转换为压应力的过程中，压痕逐渐由凹陷转为堆积。

图2-4　压头压入材料后表面形貌图［16］

对于恒定压痕深度h1，拉应力、无应力和压应力状态的载荷分别为FT、F0和Fc。压应力的加载曲线斜率大于无应力的，而拉应力的加载曲线斜率小于无应力的。

由于硬度不变，所以

如果将由残余应力引起的载荷差定义为Fr，则

材料内的残余应力为(www.xing528.com)

2.1.2.3　Lee理论模型Ⅱ［10］

2003年，Yun-Hee Lee等又提出了一种测量（100）钨单晶体残余应力的方法。钨单晶体中的弹性残余应力视为等双轴平面应力，即Rr，x＝Rr，y＝Rr，z＝0，将该应力分解为平均应力和偏应力，则有

偏应力部分沿压痕方向的应力元素直接加在垂直方向的应力上，因此，无应力和有应力试样的载荷差可表示为

由于压头回弹处样品材料的压痕深度和硬度不变，在残余拉应力的释放过程中，载荷由FT增大到F0时，接触面积由AT增大到Ac。连续的应力释放可以表示为

残余应力从Rr到0的释放过程被认为是线性的，即

如果除去压痕尺寸效应，那么接触面积Ac可以由载荷F来表示，而接触面积的经验拟合公式为F的三次方程，拟合常数为R0、R1、R2、R3，则有

将式（2-35）和式（2-36）代入式（2-34）可得

2.1.2.4　Lee理论模型Ⅲ［11］

2004年，Yun-Hee Lee等建立了测量二维平面应力的方法，将应力状态划分为四类，即单轴应力）、等双轴应力、双轴应力和纯切应力）。将等双轴主应力元素用表示，另一个应力元素用表示（表2-1）。其中可以用来表示，，k的范围为－1.0（纯切应力）～0（单轴应力）～1.0（等双轴应力）。

表2-1　无应力和人为施加应力时压痕载荷曲线分析［11］

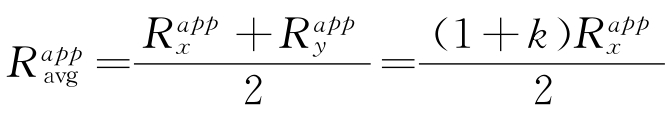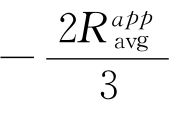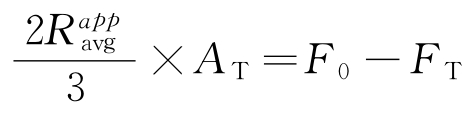因为平均应力，并且Lee理论模型Ⅱ中的偏应力元素为，而，所以。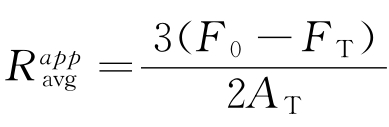

因此残余应力模型为

2.1.2.5　模型之间的联系［2］

通过以上对各种理论模型的详细介绍，可以发现它们之间的联系。如果将各模型的原理用矩阵的形式表示，则各模型及其测量公式表示如下。

Suresh模型可以表示为

Lee理论模型Ⅰ可以表示为

Lee理论模型Ⅱ可以表示为

Lee理论模型Ⅲ可以表示为

对比式（2-40）和式（2-41），可以发现对于拉应力而言，固定压痕深度时Suresh模型与Lee理论模型相同，而压应力情况则相差一个系数sinα。Lee理论模型Ⅱ的测量结果约为Lee理论模型Ⅰ的3/2，这是因为两种模型考虑的从FT到F0的卸载方式不同，模型Ⅰ认为在卸载过程中残余应力不变，而模型Ⅱ认为是线性卸载，残余应力在此过程中从最大值线性变为零。当k＝1时，Lee理论模型Ⅲ就是Lee理论模型Ⅱ。

上述所有理论模型均采用球形、圆锥形和棱锥形对称压头，并将残余应力假设为等轴的或不等轴的表面应力，且仅能测量平均残余应力的大小，而残余应力的方向和每个方向上残余应力的大小还无法确定。这些都阻碍了用纳米压痕技术去测量复杂表面残余应力的发展。

2.1.2.6　Swadener理论

Swadener理论以使用球形压头为前提，因球形压头有确定的变形范围，用其计算残余应力比用尖锐的锥形压头精确得多。Aljat等已经成功地用球形压头测量了抛光铝合金的表面应力，并分析了产生测量误差的原因［17］。他们发现存在残余拉应力时纳米压痕载荷-位移曲线会倾向于得到大的压入深度，存在压应力时则相反。图2-5为施加不同应力下的平均接触应力与无量纲接触半径Era/（RyieldR′）的关系。根据以上发现，他们研究了两种用球形压头测量残余应力的方法［7］。

图2-5　双轴残余应力对平均接触压力的影响［6］

（1）第一种方法。依据材料受应力影响刚开始屈服时，测量深度和接触半径可用Hertzian接触力学分析的理论，对于球形压头提出的残余应力计算公式为

式中，R为压头半径；a为接触半径；Ry为屈服应力。很显然，只要获得独立可估算的屈服强度，即可用式（2-44）计算残余应力。

（2）第二种方法。Tabor提出硬度和屈服强度之间的关系式为H＝kRy（k为常数因子），对于存在残余应力的材料来说，该式应该修正为H＋Rr＝kRy。如果已知参考试样的应力状态，kRy的变化和Era/（RyR）可由实验得到，式（2-44）即可用来计算残余应力。

球形压头测残余应力的理论中第一种方法要求单独测量材料的屈服应力，而第二种方法要知道参考试样的应力状态，因此需要做额外的实验来对其进行测量，并且此项技术应用于薄膜材料残余应力的测量方面存在困难［18］。