2014环保工程师资格考试知识点分析

1.流动相似

要保证两个流动问题的力学相似，要求两个流动几何相似、运动相似、动力相似，以及两个流动的边界条件和起始条件相似。

（1）几何相似 几何相似是指流体流动空间的几何相似，即两个流动空间的对应线段长度成比例，对应角度相等。用下标“n”表示原型流场各参数，用下标“m”表示模型流场各参数。如图10-43所示，几何相似要求弯管的转弯角度相等，即θ_n=θ_m，对应的几何长度成比例，即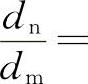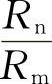。各对应线段长度比例均相等，可以写成

式中比例常数λ_l称为长度比例常数或长度比尺。几何量除长度外还有面积和体积，显然，两相应面积之比为长度之比的平方，对应流场空间的体积之比为长度之比的立方，分别称为面积比例常数和体积比例常数。

几何相似是力学相似的前提条件。

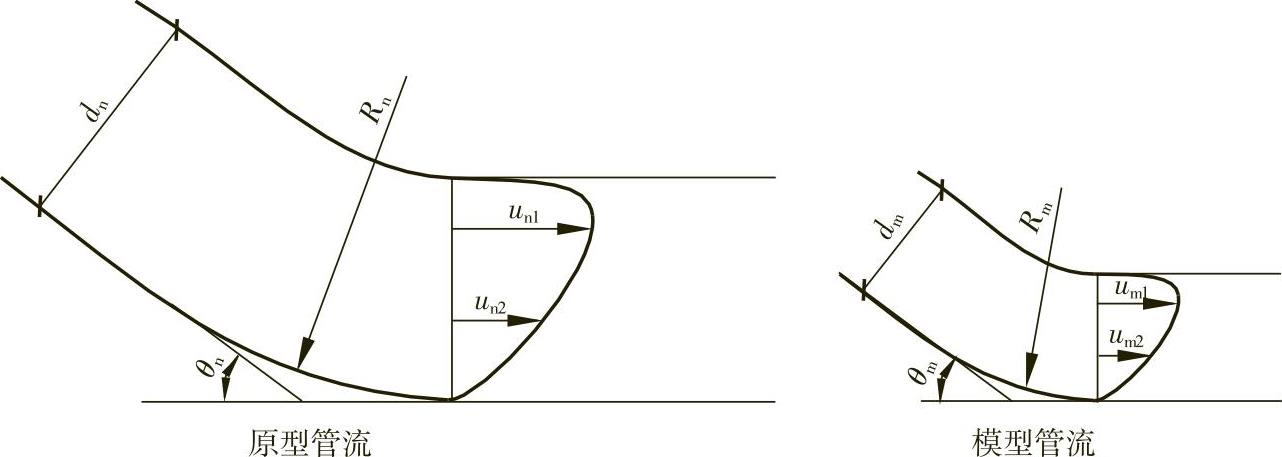
图10-43 几何相似与运动相似

（2）运动相似 两个流场的运动相似是指对应点的流速分别成比例，且要求对应点的速度方向相同，如图10-43所示，即

式中，λ_u称为速度比例常数。由流线的概念可知，运动相似意味着两流场中流线的几何相似。式（10-58）中υ_n/υ_m是对应断面的平均流速之比。运动量除速度以外还有时间和加速度，根据速度的定义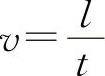，流体质点在两组对应点之间运动所花的时间分别为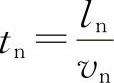和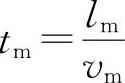，两者的比例为

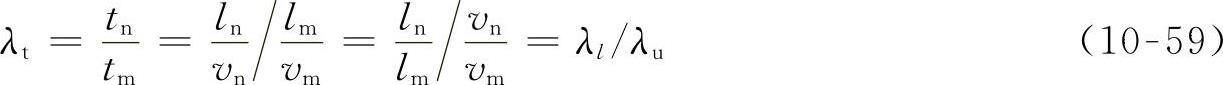
式中，λ_t称为时间比例常数或时间比尺。

加速度的定义为单位时间内的速度变化量

两者的比例为

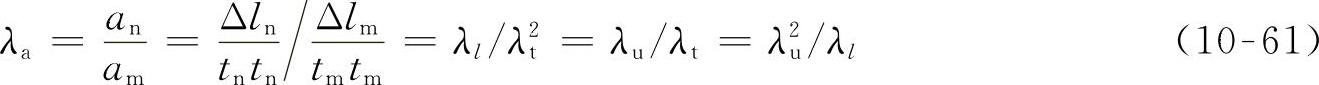
在几何相似的流场中，λ_l为常数，运动相似时λ_u为常数，所以加速度比例λ_a也是常数；反之，加速度比例为常数时，速度比例也为常数，流动是运动相似的，这个结论对讨论运动相似的条件很重要。

通过运动相似对应点的速度或断面平均流速成比例这一结论，可以根据模型试验测得的模型流速推算出原型对应点的流速或断面平均流速，这正是模型试验所要解决的主要问题，所以说运动相似是相似研究的目的。

（3）动力相似 流动的动力相似要求作用于相应点流体质点的同名作用力成比例。即：原型流动和模型流动对应点处流体质点所受的重力、压力、黏性力、惯性力、弹性力等作用力分别成比例，即

式中，T、P、G、E、I分别表示黏性力、压力、重力、弹性力和惯性力。设黏性力、压力、重力、弹性力的合力为F，惯性力与合力F互为反力。根据牛顿第二定律，合力与加速度成正比，所以合力成比例则加速度成比例。而根据运动相似的结论，加速度成比例则速度成比例。所以，只有动力相似才可以实现加速度的相似，进而实现运动相似，即：动力相似是相似的保证。

（4）初始条件与边界条件的相似 对于非恒定流问题，某时刻流场速度分布显然是与初始速度分布有关的，所以只有运动的初始条件相似，才有可能实现对应时刻的运动相似。而对于恒定流或近似恒定流的情况，可以不考虑初始条件的影响。

2.相似准则

要使两个流动动力相似，需要两流动相应点上的力多边形相似，相应边（同名力）成比例，由此得到各单项力的相似准数。以下标“n”表示原型，下标“m”表示模型。(www.xing528.com)

（1）雷诺准则 取两流动对应点上的惯性力与黏滞力，建立对比关系如下

由于是对比关系，而不是计算力的绝对量，所以式中的力可以用流动的特性量来表示，例如：惯性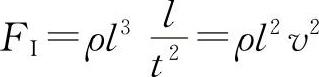力黏滞力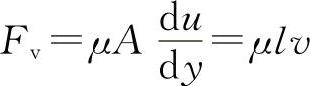代入式（10-63）整理，得

无因次数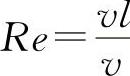

就是雷诺数。它表征惯性力与黏滞力之比，两流动相应的雷诺数相等，黏滞力相似，这一准则称为雷诺准则或黏滞力相似准则。

（2）弗劳德准则 同理选取特征量重力F_G=ρgl³，取两流动对应点上的惯性力与重力对比，有

无因次数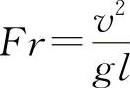称为弗劳德数。它表征惯性力与重力之比，两流动相应的弗劳德数相等，重力相似。这一准则称为弗劳德准则或重力相似准则。

（3）欧拉准则 选取特征量压力F_p=Δpl²，两流动对应点上的压力与惯性力对比，有

无因次数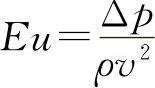称为欧拉数。它表征压力与惯性力之比，两流动对应的欧拉数相等，压力相似。这一准则称为欧拉准则或压力相似准则。

3.方程和因次分析法

（1）方程 一个正确的物理方程，其各项的量纲（因次）是一致的，称之为量纲（因次）和谐原理，利用量纲和谐原理可以推求物理过程参数间的关系，称为量纲（因次）分析法。

（2）因次分析法 在因次和谐原理基础上发展起来的因次分析法有两种，一种称为瑞利法，适用于比较简单的问题；另一种为π定理，是一种具有普遍性的方法。

4.流体力学模型研究方法

模型试验是依据相似原理，制成和原型相似的小尺度模型进行试验研究，并以试验的结果预测出原型将会发生的流动现象。进行模型试验需要解决下面两个问题。

（1）模型律的选择 为了使模型和原型流动完全相似，除要几何相似外，各独立的相似准则应同时满足。但实际上要同时满足各准则数很困难，一般只能达到近似相似，就是保证对流动起重要作用的力相似，这就是模型律的选择。如有压管流，黏滞力起主要作用，应按雷诺准则设计模型；在大多明渠流动中，重力起主要作用，应按弗劳德准则设计模型。

（2）模型设计 进行模型设计，通常先根据试验场地、模型制作和测量条件定出长度比尺；再以选定的比尺缩小原型的几何尺寸，得出模型的几何边界；根据对流动受力情况的分析，满足对流动起主要作用的力相似，选择模型律；最后按选用的模型律，确定流速比尺及模型的流量。

5.试验数据处理方法

依据相似准则设计的模型试验过程，可以保证原型流动与模型流动的运动相似。试验数据处理是根据式（10-58）、式（10-59）以及各准则数对应的方程预测原型运动参数的过程，也可以通过各准则数对应的方程求取原型上的各类作用力。

【例10-2】 长度比例常数为50的船模型，在水池中以1m/s的速度牵引前进，测得波阻力为0.02N，假定摩擦阻力和形状阻力都比较小，可以忽略不计。求原型船所受的波阻力。

【解】波动主要受重力的影响，与黏性关系不大，所以选用弗劳德准则，有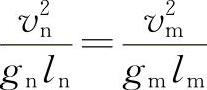取g_n=g_m，原型流速为。

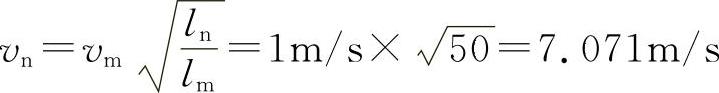由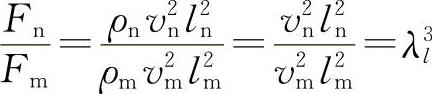，原型船所受的波阻力为F_n=λ_l³F_m=50³×0.02N=2500N。