2014环保工程师考试专业基础知识点+训练

1.层流与紊流、雷诺数

层流为各流层质点互不掺混，分层有规则的流动状态；紊流为流体质点互相强烈掺混、运动极不规则的流动状态，又称紊流。层流与紊流流动状态简称为流态。

圆管内流态的判别条件是雷诺数Re。

式中 Re——雷诺数，无量纲；

υ——管内平均流速（m/s）；

d——管道内径（m）；

υ——管内流体的运动黏性系数，又称运动黏度（m²/s）。

Re_K=2000，是圆管流的临界雷诺数值。层流：Re<2000，紊流：Re>2000。

层流和紊流的根本区别在于层流各流层间互不掺混，只存在黏性引起的各流层间的滑动摩擦阻力；紊流时则有大小不等的涡体动荡于各流层间，除了黏性阻力，还存在着由于质点掺混、互相碰撞所造成的惯性阻力，也称为雷诺切应力。因此，紊流阻力比层流阻力大得多。

雷诺数反映惯性力和黏性力的比值。

2.流动阻力分类

在管径与粗糙度不变的管段上，单位管长的流动阻力也不变，称这类阻力为沿程阻力。克服沿程阻力引起的能量损失称为沿程损失，常用的是沿程水头损失，符号为h_f，单位是m。

在边界急剧变化的区域，阻力主要集中在该区域内及其附近，这种集中分布的阻力称为局部阻力。克服局部阻力的能量损失称为局部损失，常用的是局部水头损失，符号为h_m，单位是m。

整个管路的能量水头损失等于各管段的沿程水头损失和各局部水头损失的总和。即

h_l=∑h_f+∑h_m （10-12）

沿程水头损失计算公式为

式中λ——沿程阻力系数，无量纲，是沿程损失计算的关键；

l、d——管长和管径（m）；

υ——管内平均流速（m/s）；

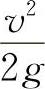——速度水头。

式（10-13）表明，沿程水头损失与速度水头成正比。

局部水头损失计算公式为

式中ζ为局部损失系数，无量纲，是局部损失计算的关键；其余符号同前。

式（10-14）表明，局部水头损失也与速度水头成正比。

3.层流和紊流沿程阻力系数的计算

圆管层流的沿程阻力系数为

它表明圆管层流的沿程阻力系数仅与雷诺数有关，而与管壁粗糙无关。

一般来讲，影响沿程阻力系数λ的因素是雷诺数和相对粗糙度，即

尼古拉兹对人工粗糙管的试验表明，沿程阻力系数λ的变化可归纳如下：

Ⅰ层流区 λ=f₁（Re）

Ⅱ临界过渡区 λ=f₂（Re）

Ⅲ紊流光滑区 λ=f₃（Re）

Ⅳ紊流过渡区 λ=f₄（Re，K/d）

Ⅴ紊流粗糙区（阻力平方区） λ=f₅（K/d）

关于λ值的计算公式主要有：

1）紊流光滑区的布拉修斯公式

2）紊流粗糙区的希弗林松公式

3）克列伯洛克公式 (www.xing528.com)

4）阿里特苏里公式

【例10-1】 管道的长度不变，允许的水头损失h_f不变，若使管径增大一倍，不计局部损失，流量增大几倍，试分别讨论下列三种情况：

1）管中流动为层流，。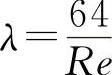

2）管中流动为紊流光滑区，。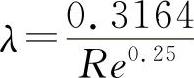

3）管中流动为紊流粗糙区，。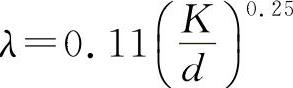

【解】管中流动为层流，则有

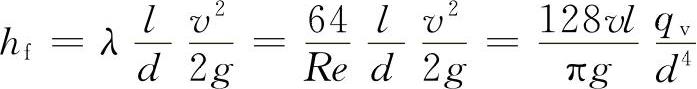
令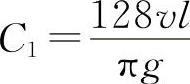，则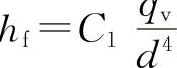。可见层流中若h_f不变，则流量q_v与管径的四次方成正比。即

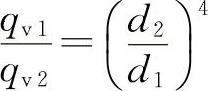
当d₂=2d₁时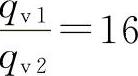，，q_v2=16q_v1

层流时管径增大一倍，流量为原来的16倍。

管中流动为紊流光滑区

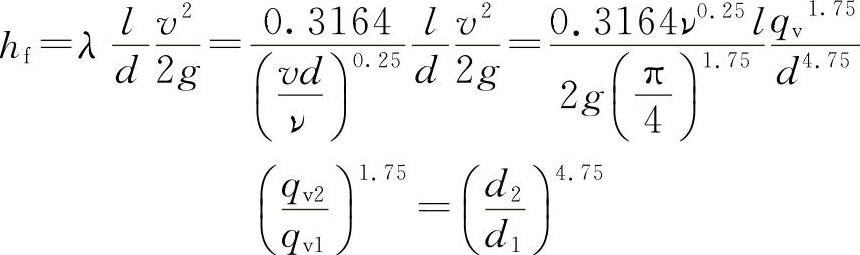
当d₂=2d₁时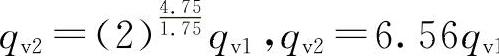，管中流动为紊流粗糙区

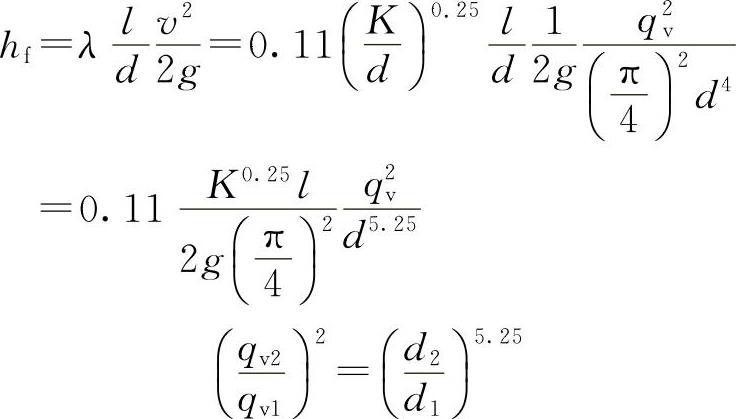
当d₂=2d₁时，，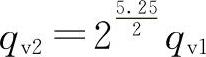

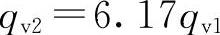
4.局部阻力产生的原因和计算方法

与沿程水头损失相似，局部水头损失也用流速水头的倍数来表示，即

局部阻碍的种类虽多，如分析其流动的特征，也不过是过流断面的扩大或收缩、流动方向的改变、流量的合入与分出等几种基本形式，以及几种基本形式的不同组合。

下面列出几种典型的局部阻力系数。

1）突然扩大管

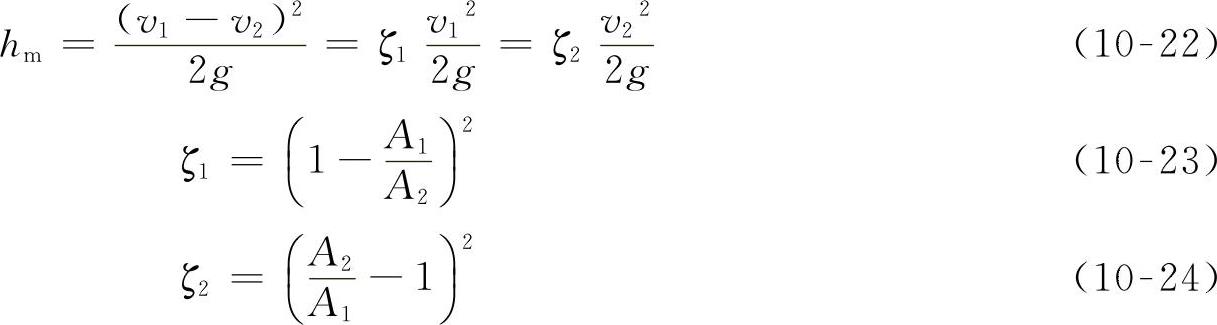
当液体从管道流入断面很大的容器中或气体流入大气时，A₁/A₂≈0，ζ₁=1。

2）突然缩小管，对应流速水头为缩小后速度水头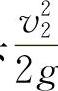，则有

当流体由断面很大的容器进入无圆角的管道时，A₂/A₁≈0，ζ=0.5。

5.减少局部阻力的措施

减小紊流局部阻力的措施主要有：

1）适当加大管径，由于局部损失与速度水头成正比，加大管径则速度水头显著减小，局部阻力随之减小，但要以牺牲材料和空间为代价。

2）通过优化设计减小局部损失。例如：用逐渐扩大、缩小或分级扩大、缩小来代替突然扩大、缩小（图10-13），可以有效减小局部损失；为减小弯管因二次流产生的损失，可以在弯管处设置导流板（图10-14）；扩大或缩小与转弯在一起时，将转弯设置在粗管段时的损失小（图10-15）；流线形进口的损失要小于直管管道进口（图10-16），锥形管道进口也有较小的损失。

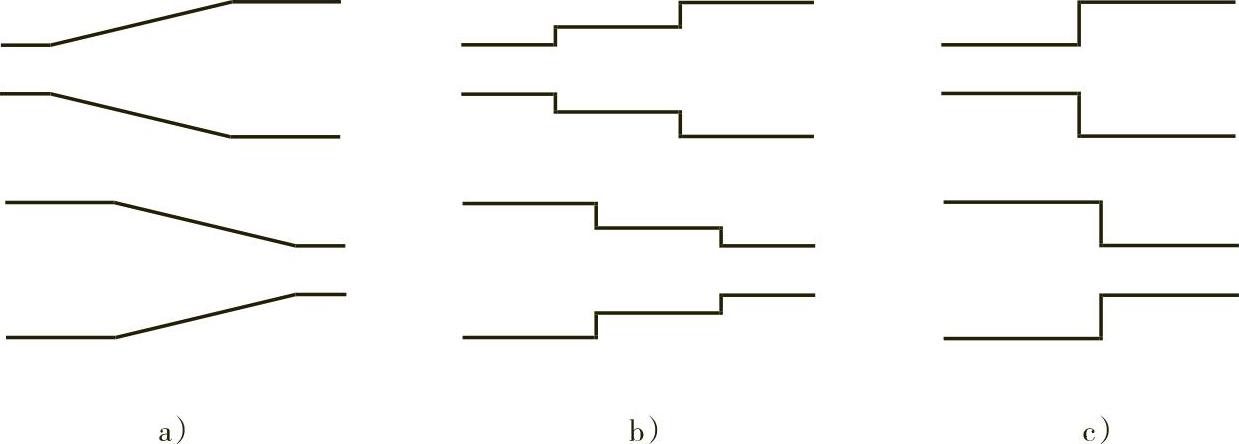
图10-13 扩大和缩小的形式

a）尺寸渐变（好） b）分级扩大缩小（较好） c）尺寸突变（差）

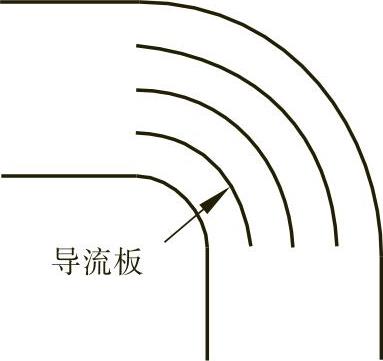
图10-14 大尺寸矩形弯道中的导流板

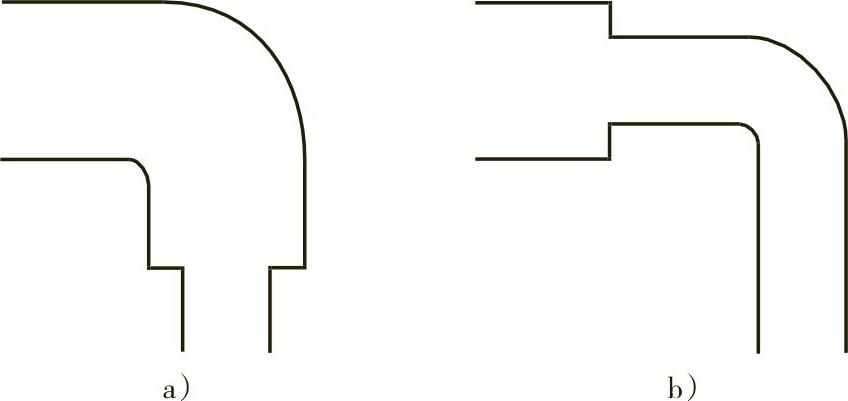
图10-15 扩大与转弯的组合

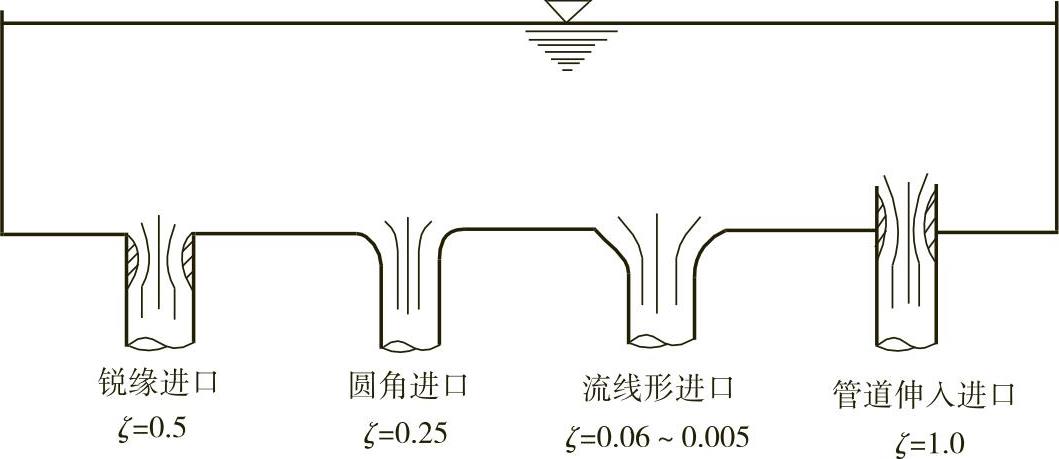
图10-16 几种管道进口的局部损失

a）先弯后缩（好） b）先缩后弯（差）