2014年环保工程师考试：知识点精析与训练

1.恒定流动与非恒定流动

描述流体运动时，如果各运动参数既是空间坐标的函数，又是时间的函数，这样的流动称为非恒定流动。运动参数以速度为例。

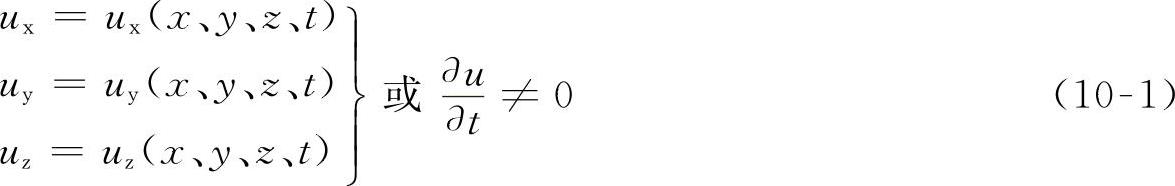
式（10-1）不仅反映了流速在空间的分布，也反映出流速随时间的变化。

如果流场中各点流速不随时间变化，由流速决定的压强、黏性力和惯性力也不随时间变化，这种流动称为恒定流动。

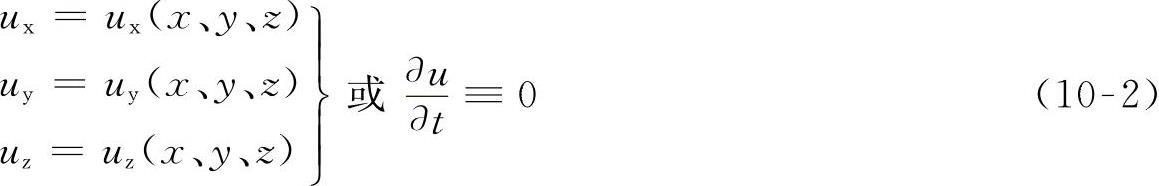
图10-1所示是恒定流与非恒定流示例，左图有水不断地补充进水箱，使水箱水位恒定，则出流流速及流量不随时间的变化而变化，为恒定流；右图没有水补充进水箱，随时间的推移水面不断下降，出流的流速及流量也会不断减小，为非恒定流。

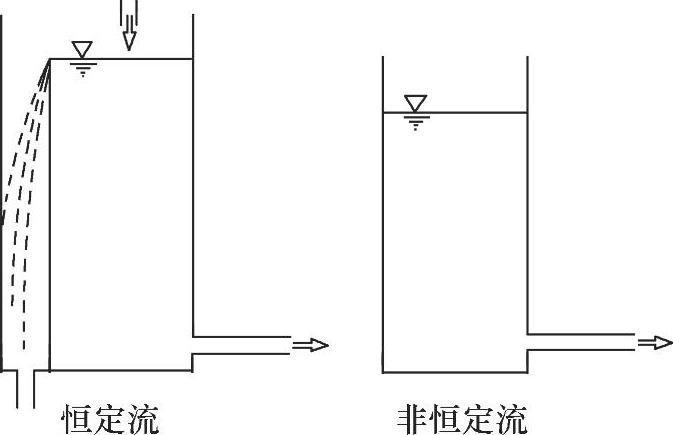
图10-1 恒定流与非恒定流

2.伯努利方程式及其使用条件

伯努利方程式又称为能量方程。

（1）理想流体恒定元流的伯努利方程 在流场中选取元流，如图10-2所示。在元流上沿流向取1-1、2-2两断面，两断面的高程和面积分别为z₁、z₂和dA₁、dA₂，两断面的流速和压强分别为u₁、u₂和p₁、p₂，有

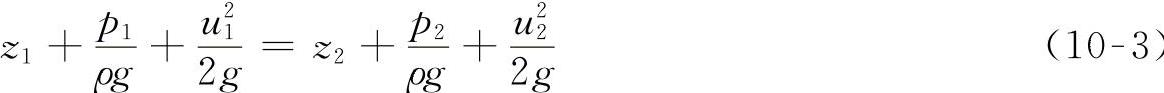
这就是理想不可压缩流体恒定元流能量方程，或称为伯努利方程。其应用条件是：理想流体、恒定流动、质量力仅为重力、沿元流（流线）、不可压缩流体。

式（10-3）中各项值都是断面值，其几何意义和物理意义分述如下：

z是断面相对基准面的高度，称为位置水头，表示单位重量流体的位置势能，简称位能。

p/ρg是断面压强作用使流体沿测压管所能上升的高度，称为压强水头，表示单位重量流体的压强势能，简称压能头。

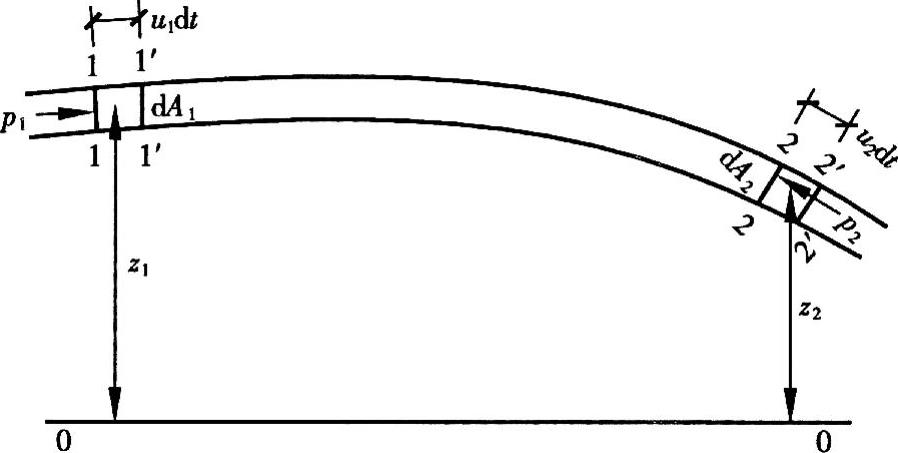
图10-2 元流能量方程

u²/2g是以断面流速u为初速的垂直上升射流所能达到的理论高度，称为流速水头，表示单位重量的动能，简称动能头。

前两项相加，以H_P表示

H_P表示断面测压管水面相对于基准面的高度，称为测压管水头，表明单位重量流体具有的势能，简称为势能头。

三项相加，以H表示

H称为总水头，表示单位重量流体具有的总机械能，简称为总能头。

能量方程式表明，理想不可压缩流体恒定元流中，各断面总水头相等，或单位重量流体的总机械能保持不变。

（2）实际流体恒定元流的能量方程 在实际流体的流动中，黏性阻力做负功，使机械能沿流向不断衰减。符号h′_l1-2表示元流1-1、2-2两断面间单位能量的衰减，称为水头损失。则能量方程式将改变为

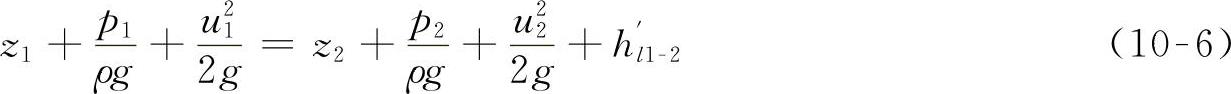
（3）实际流体恒定总流能量方程 质点流速的大小和方向均不变的流动称为均匀流动，反之为不均匀流动。不均匀流动又按流速随流向变化的缓或急，分为渐变流动和急变流动，如图10-3所示。(www.xing528.com)

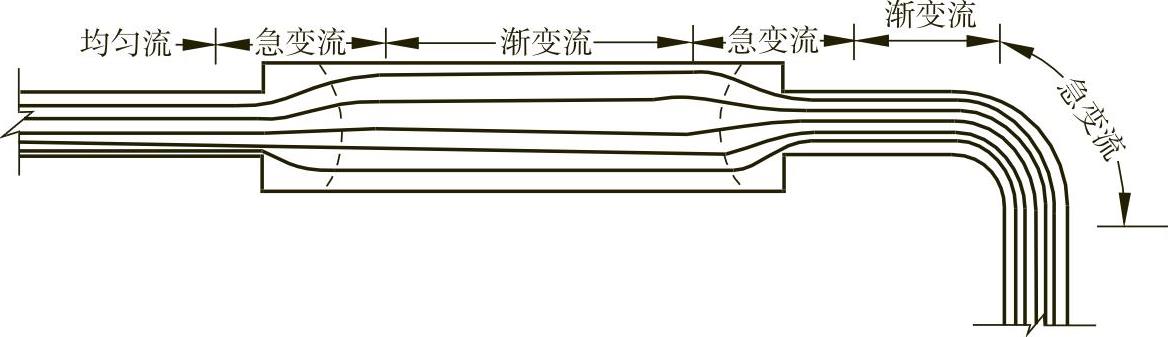
图10-3 均匀流和不均匀流

均匀流的流线是相互平行的直线，因而它的过流断面是平面。在断面不变的直管中的流动，是均匀流动最常见的例子之一。

在均匀流过流断面上，压强分布符合静压基本方程，即

渐变流的流线近乎平行直线，流速沿流向变化所形成的惯性小，可忽略不计。渐变流过流断面可近似认为是平面，在过流断面上，压强分布也可认为服从于流体静力学规律。也就是说，渐变流可近似地按均匀流处理。

在流动上下游选取两个均匀流或渐变断面1-1和2-2，有

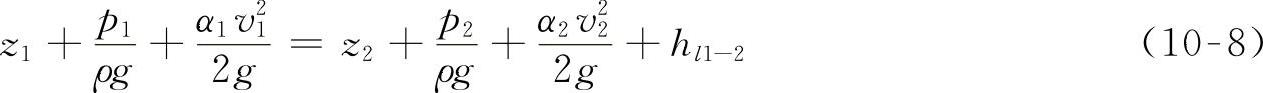
这就是极其重要的恒定总流伯努利方程式，或称恒定总流能量方程式。

式中 z₁、z₂——选定的1-1、2-2渐变流断面上任一点相对于选定基准面的高程（m）；

p₁、p₂——计算断面对应点的压强（Pa），使用相对压强或绝对压强均可；

υ₁、υ₂——相应断面的平均流速（m/s）；

α₁、α₂——计算断面的动能修正系数，无量纲，通常为简化取α=1.0；

h_l1-2——1-1、2-2两计算断面间的平均单位水头损失（m），两计算断面应为均匀流或渐变流断面。

3.总水头线和测压压管水头线

图10-4所示是典型的总水头线和测压管水头线，需要注意的有以下几点：①由于有沿程损失和局部损失的存在，总机械能沿程减小，总水头线总是沿程下降的。而由于能量之间存在转化关系，测压管水头可以上升，也可以下降。②有局部损失的地方总水头突然下降。③等管径的地方总水头线与测压管水头线两线平行，间距为速度水头。④流量及粗糙度相同条件下，管径小处水头线斜率较大。

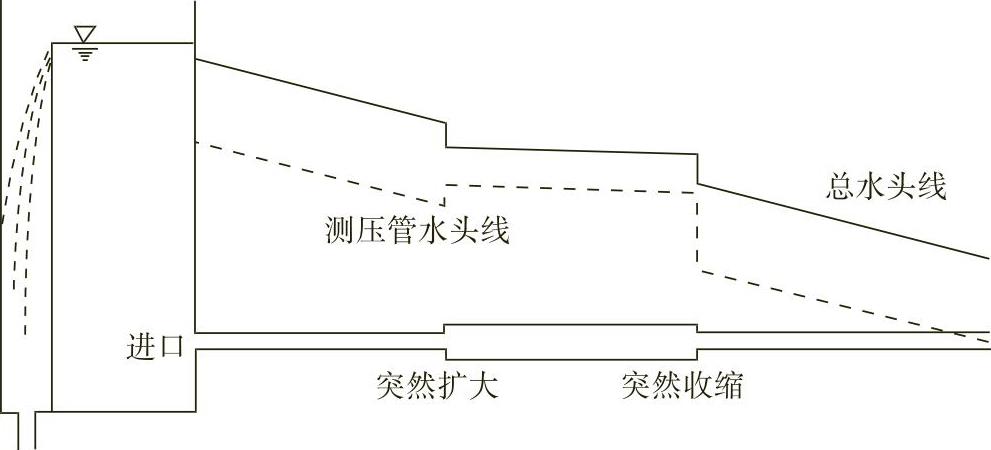
图10-4 总水头线和测压管水头线

4.总压线和全压线

对于高差较大的气体流动，气体密度和空气密度不等的情况下，须考虑大气压强因高度不同的差异。气流能量方程可写成

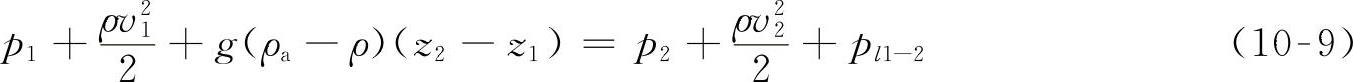
式中，p为静压；ρυ²/2为动压，两者之和p_q=p+ρυ²/2，称为全压；g（ρa-ρ）为单位体积气体所受的有效浮力；（z₂-z₁）为气体沿浮力方向升高的距离，乘积g（ρa-ρ）（z₂-z₁）为1-1断面相对2-2断面单位体积气体的位能，称为位压；静压与位压相加p_s=p+g（ρ_a-ρ）（z₂-z）称为势压；p_z=p+ρυ²/2+g（ρ_a-ρ）（z₂-z）称为总压，p_l1-2为两断面间的压强损失。

沿流程将全压p_q=p+ρυ²/2和总压p_z=p+ρυ²/2+g（ρ_a-ρ）（z₂-z）数值的大小分别用几何图线表示出来，即为全压线和总压线。

图10-5所示为气流的静压线、全压线、位压线和总压线：图10-5a表示气流从静压箱A沿管路排向高空，管外为空气。图10-5b～d中ABC表示压强基准线，是A、B、C各点管道外的大气相对压强，显然都是零；图10-5b表示管中气体与管外均为空气时的情况，由于内外气体密度一致，式（10-9）简化为

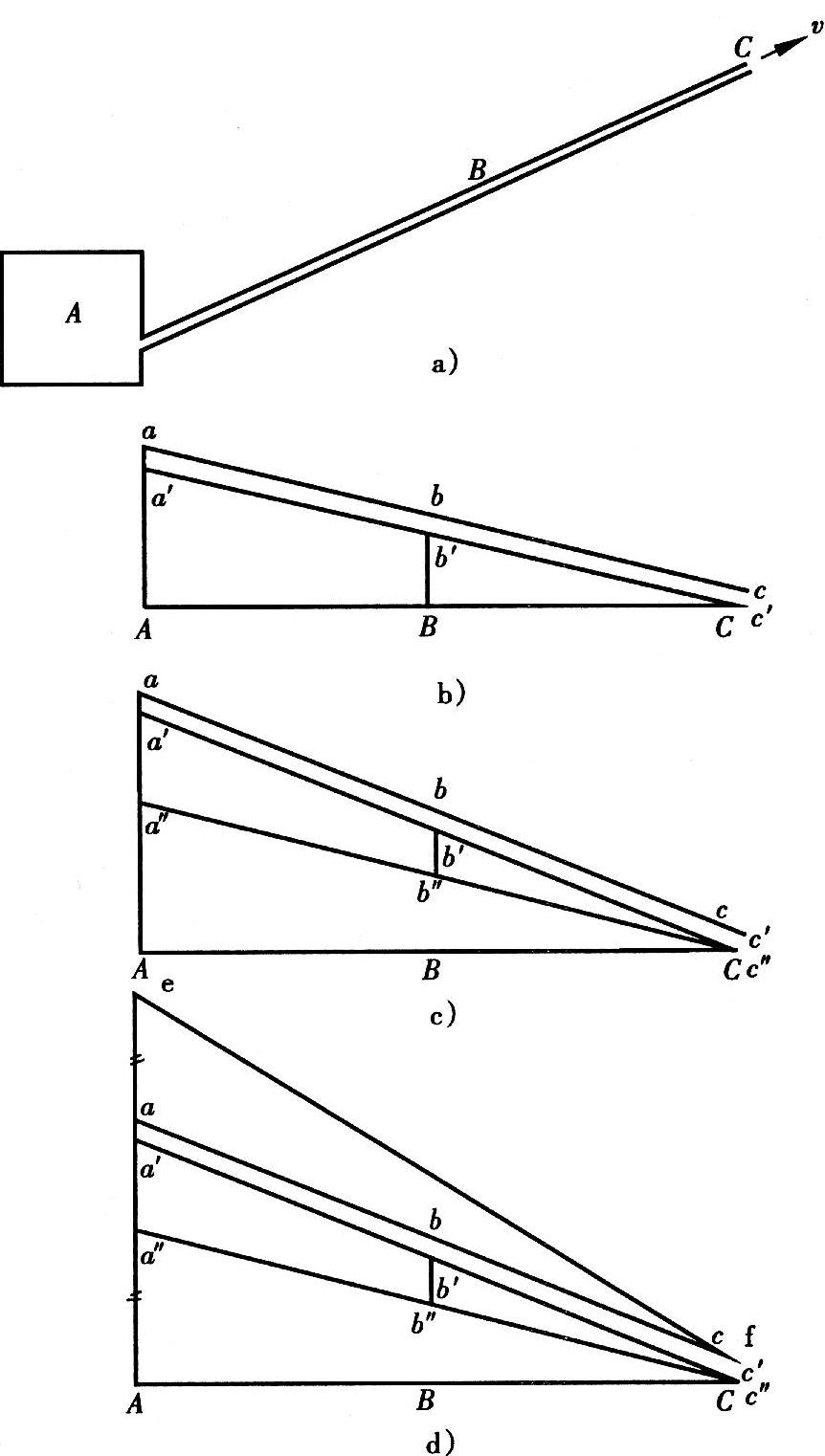
图10-5 静压线、全压线、位压线和总压线

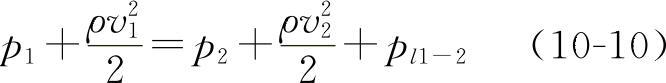
图10-5中a′c′为静压线，ac为全压线，两者之差为动压ρυ²/2，由于不存在位压，所以ac也是总压线；图10-5c、d中管内气体密度小于管外空气密度，例如煤气的情况，a′c′为静压线，ac为全压线，两者之差为动压ρυ²/2，存在位压g（ρa-ρ）（z_c-z），a″c″为位压线，注意位压是相对出口C点高度z_c的，z越小则位压越大，将位压线a″c″叠加到全压线ac上方，得到图10-5d中的总压线ef。