信号重构算法：高等色度学

压缩感知理论中最后一个问题是信号重构，是指通过压缩感知重构算法从少量的测量值中恢复出原始信号的过程。压缩感知信号的测量过程是降维处理，即亚采样过程，也就是说测量方程数小于未知数，理论上存在无数个解。压缩感知要求原始信号本身具有显著稀疏性或在某个变换域下具有显著稀疏性，这从本质上为求解此类方程组提供了可能。压缩感知相关定理为近似或精确求解提供了理论上的保证，只要在线性观测过程中没有破坏原始信息，那么就可以通过算法从测量值中精确恢复原始信号。现在需要考虑的问题是，如果给定了压缩采样值，什么算法能够有效地重建信号。实用的压缩感知重建算法应该具有如下的性质:能够接受不同的采样体系获得的采样值；能用最少的采样率实现成功的重建；当采样值中包含噪声时，它是鲁棒的；有一定的重建准确性；有足够的效率。

针对信号重构的算法目前可主要分为凸优化算法、贪婪算法和组合算法三类。凸优化算法针对线性规划最优化问题寻求信号的逼近，将非凸问题转化为凸问题求解，常用的有基追踪算法、内点法、迭代阈值算法和梯度投影算法等。贪婪算法通过每次迭代时选择一个局部最优解来逐步逼近原始信号，这类算法主要有匹配追踪系列算法，如正交匹配追踪算法、分段正交匹配追算法、正则化正交匹配追踪算法等。凸优化算法重构质量好，所需测量次数少，但是计算复杂度较高；贪婪算法计算复杂度相对较低，但是需要更多的测量次数，重构精度也不如前者。每种算法都有各自的优点及固有的不足之处，而且严格的理论支撑也需要进一步完善，因此构建稳定有效、鲁棒性好，同时所需较少压缩测量的算法是压缩感知需要克服的瓶颈之一。

进行重构时应在充分考虑信号特征的情况下选择重构算法，大多数自然图像的离散梯度是稀疏的，基于此，Candes 等人提出了更适合二维图像重构的最小全变差算法:

其中，TV(x)为全变差，表示图像的离散梯度。全变差作为一种稀疏变换常用于图像处理，具有限制高频分量和去噪的能力，适用于目标和背景具有平滑特征的图像。

凸优化算法:在稀疏重建模型中，Candès 指出可以把复杂性和不稳定性较高的l0 范数最优化问题转化为等价的l1 范数最优化问题，通过不断寻找l1 范数最小的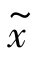 来逼近压缩采样得到的信号y，当l1 范数不再减少时，方程组求解成功。这种思路就引出了著名的基追踪方法(Basis Pursuit，BP)，其计算复杂度为O(N3)[224]。2007年，Figueiredo 等人在梯度下降法的基础上提出了著名的稀疏梯度投影法(Gradient Projection for Sparse Reconstruction，GPSR)，该算法受初始值的影响较小，而且通过调整正则因子可以有效提升算法的重建速度[241]。此外，典型的凸优化算法还包括迭代收缩算法(Iterative Shrinkage Thresholding Algorithm，ISTA)[242]、快速迭代收缩算法(Fast Iterative Shrinkage Thresholding Algorithm，FISTA)[243]、分裂Bregman 迭代算法(Split Bregman Iteration，SBI)算法[244]和交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)[245]等。

贪婪算法:贪婪算法出现的时间较早，解决的是最小l0 范数问题，求解时利用迭代算法通过减少残差寻找信号或图像的最稀疏表示。最典型的贪婪算法是匹配追踪算法(Matching Pursuit，MP)，由Mallat 等人[246]提出。随后，Troppj 引入正交的思想，通过递归对已选择原子集合进行正交化以保证迭代的最优性，提出了正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)[229]。为了缩小运算时间，提高重建精度，增强重建信号对噪声的鲁棒性，2009年Needell 等人在OMP 的基础上提出了正则正交匹配追踪(Regularized Orthogonal Matching Pursuit，ROMP)算法[247]和压缩采样匹配追踪(Compressive Sampling Matching Pursuit，CoSaMP)算法[248]。Donoho 等人提出了一种对稀疏度K 自适应的稀疏自适应匹配追踪(Sparsity Adaptive Matching Pursuit，SAMP)算法[249]，可以在K 未知的情况下获得较好的重建效果，速度也远快于OMP 算法。

组合算法:该类算法是由组测试演变出来的，要求信号的采样数据可以通过分组测试快速重建。该类算法包括随机傅里叶采样方法、稀疏序列匹配追踪算法、计数－最小略图法和计数－中值略图法等。

以下重点介绍匹配追踪算法(MP)、正交匹配追踪算法(OMP)和正则化正交匹配追踪算法(ROMP)。

1.匹配追踪算法

匹配追踪算法，其核心思想是把一个信号用超完备字典ΦϵRM×N 中的元素进行线性表出，然后对信号进行稀疏逼近。MP 算法是针对残差rϵRM 来展开的，每次迭代选取于当前残差相关性最高的原子:

式中，φλ 表示矩阵Φ 的第λ 列；rk 表示残差；k 表示迭代次数。然后把选出的相关性最大原子放入支撑集中，并用支撑集中的原子进行重构，用得到的重构向量求出新的残差，具体表示如下:

随后进行下次迭代，直到满足停止迭代条件，输出信号的稀疏逼近。最后得到的稀疏逼近即为原信号的线性表示，用于求解原信号。具体步骤如下:

输入:测量矩阵A，观测矩阵y，稀疏度K

输出:信号稀疏逼近

(1)初始化:r0＝y，Λ0＝，k＝1；

(2)找出与残差匹配度最高的原子λk＝；

(3)更新θk＝θk－1＋〈rk－1，φλk〉；

(4)更新残差rk＝；

(5)判断是否满足k >K 或者，若为真则停止迭代，否则k＝k＋1 并返回步骤(2)。

匹配追踪算法在重建原始信号的算法中，性能稳定，理论简单，然而在使用的过程中无法保证重构精度，这对重构算法是致命的打击，而且信号和每次选择的原子是非正交的，这就导致每次选择的原子可能不是最优的，为了得到较好的逼近就需要进行多次迭代。

2.正交匹配追踪算法

针对匹配追踪算法重构精度低、迭代次数多的问题，研究人员提出了正交匹配追踪算法(OMP)。正交匹配追踪算法很好地解决了MP 算法在重构时的问题，该算法采用了MP 算法原子选取的原则，但是对选取的原子进行正交处理，这样就保证了每次选择原子的最优性，加快了算法的收敛，减少了迭代次数，提高了算法精度。

匹配追踪类算法通过求残差r 与感知矩阵Φ 中各个原子之间内积的绝对值，来计算相关系数u:

并采用最小二乘法进行信号逼近以及残差更新:

通过上述过程进行一次次迭代，直到满足收敛条件，这个方法称为正交匹配追踪算法。假设原始的待测信号是稀疏的，同时测量矩阵中每个元素都是从一个服从亚高斯分布的变量中随机选取的，则基于线性混叠的有限个测量值，通过OMP 算法实现以极大的概率重构出原始的稀疏信号。这个算法最多需要K 次循环即可收敛，其中K 为原始信号的稀疏度；其缺点是在每次循环中，需要额外的正交化运算。和MP 算法相比，在精度要求相同的情况下，OMP 的收敛速度更快。(www.xing528.com)

OMP 算法具体步骤如下。其中rt 表示残差，t 表示迭代次数，J 表示每次迭代找到的列序号，At 表示按索引Λt 选出的矩阵A 的列集合。

输入:测量矩阵A，观测矩阵y，稀疏度K

输出:信号稀疏逼近

(1)初始化:r0＝y，Λ0＝，t＝1；

(2)找出与残差匹配度最高的原子并放入支撑集中，；

(3)更新索引集；

(4)求最小二乘解，得到重构向量；

(5)更新残差rt＝y－Atθt；

(6)判断是否满足t>K 或者，若为真则停止迭代，否则t＝t＋1 并返回步骤(2)。

3.ROMP 算法

Needell 和Vershynin 等人将正则化过程运用到稀疏度已知的OMP 算法中，提出了正则化正交匹配追踪算法(ROMP)，该算法相比于OMP 算法在重构效率上有明显提高。为了改进OMP 算法的缺点，Needell 等人把OMP 算法重构过程和正则化方法结合，提出了改进的正则化正交匹配追踪算法。该算法在每次迭代时，不再是只选取一个最优原子，而是选取K个；然后对选出原子按正则化方法进行二次选取，选出的原子放入支撑集。相比于OMP 算法，ROMP 算法大大加快了算法的收敛。

已知信号的稀疏度为K，计算测量矩阵和当前残差的内积，从中选取前K 个相关系数较大的原子，放入候选集J 中，如式(8－59):

上式表示在集合J 中存储K 个匹配度最高的原子的索引，其中rt－1表示第t 次迭代的残差，aj 表示矩阵A 的第j 列；然后在二次选取时再通过一个正则化过程保证入选的原子所携带的信息都接近一个均值并选出能量较大的一组原子，放入支撑集中重构原信号，而携带较少信息量的原子则被舍弃。

其中，J0 为集合J 中满足式(8－59)的原子构成的子集。ROMP 算法具体步骤如下。其中rt 表示残差，t 表示迭代次数，J 表示每次迭代找到的列序号，At 表示按索引Λt 选出的矩阵A 的列集合。

输入:测量矩阵A，观测矩阵y，稀疏度K

输出:信号稀疏逼近

(1)初始化:r0＝y，Λ0＝，t＝1；

(2)找出与残差匹配度最高的原子并放入支撑集中，；

(3)按正则化for all i，j∈J0 找出J 中平均能量最高的子集J0；

(4)更新索引集，At＝At－1∪aj；

(5)求最小二乘解，得到重构向量；

(6)更新残差rt＝y－Atθt；

(7)判断是否满足t>K 或者，若为真则停止迭代，否则t＝t＋1 并返回步骤(2)。