书名《通识物理》，矢量图解法理解简谐振动，附图7

简谐振动的定义是：“物体在回复力的作用下，在其平衡位置附近按余弦函数或正弦函数规律做周期性往复运动。”简谐振动是最基本、最简单的振动单元，任何复杂的振动其实都可以分解为若干个简谐振动的叠加；同理，不同单音（简谐振动）的叠加也会得到任何我们想要得到的声音，这也是电子合成音的基本原理。简谐振动的基本特征是“受到与位移成正比的回复力作用”，比如振子在弹簧弹力的作用下所做的往复运动，就是一种简谐振动。在我们的现实生活中，我们常见的秋千和单摆都会在重力的回复力作用下做周期性的往复运动；弹簧振子和琴弦则会在弹力的回复力作用下做周期性的往复运动。因此，秋千、单摆、弹簧振子和琴弦在起振后一段不长的时间里，其运动形式都可以看作是简谐振动。

根据简谐振动的定义，简谐振动还可以用矢量图解法进行理解。如图7.2所示，弹簧振子在竖直方向上所做的往复运动，可以看成振子在矢量图上做“逆时针”的匀速圆周运动。同时，振子的运动在位移时间（v-t）曲线图上还体现出余弦函数或正弦函数曲线的特征，而振子在三种运动图像上的位置是水平对应的。为了定量分析弹簧振子的简谐振动，我们可以用一个余弦方程（也可以采用正弦方程，但有π/2的相位差）来进行数学描述：

在构成这个余弦方程的物理量中，振幅（A）、角频率（ω）和初相位（φ0）是决定其简谐振动状态的三个重要参数（态参量）。首先，振幅（A）在振动图上表示物体离开平衡位置的最大幅度，在矢量图上表示振子做圆周运动的半径，在曲线图上则表示余弦函数或正弦函数的最大值，体现简谐振动的强弱。当我们增加振幅时，不仅可以看到弹簧振子的振动幅度明显增加，而且可以看到矢量图上振子的画圈半径也显著增大，而曲线图上函数曲线则在纵向上拉长。其次，角频率（ω）是一个描述振子做往复运动快慢的物理量。当我们增加角频率时，振子的振动速度以及在矢量图上的画圈速度都会显著变快。最后，初相位（φ0）则描述了振子的初始起振位置，决定于t=0 时的振动状态，当我们调节初相位时，将会看到振子从不同的位置开始运动（参量调节请参见本书配套慕课视频）。(www.xing528.com)

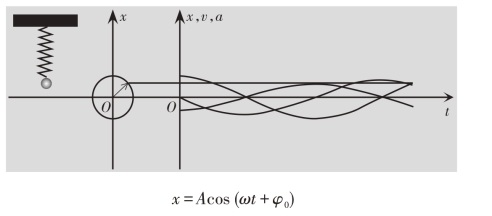
图7.2　简谐振动的振动图（左）、矢量图（中）和曲线图（右）

通常，一首音乐就可以分解为多个不同的简谐振动。有的音乐朗朗上口、悦耳动听，比如最常见的《小苹果》《青春修炼手册》等神曲；而有些音乐则曲调拗口、昙花一现。音乐的不同其实就在于其组成单元——简谐振动的“振幅、频率和初相位”不同。如果音乐家学会了简谐振动的相关知识，就可以对组乐进行研究，从而创作出更加优美的电子乐。