伯努利效应的应用及其成果

理想流体的伯努利方程主要包括三个变量：压强p、流速v和高度h。而通常，人们对三个物理量之间的变化关系难以形成一个直观的印象，比如流速增加了，压强和高度究竟该怎么变？这并没有确定的答案。为了解决这类问题，人们习惯于假定其中一个变量是恒定的，这样才能分析另外两个变量之间的变化规律。其实早在1726 年，也就是在伯努利方程提出前，伯努利通过无数次实验测量，就已经发现了等高条件下流速和压强的变化规律，即流体的“边界层表面效应”，其内容是：“当流体速度加快时，流体层界面上的压强会减小，反之压强会增加。”这个效应其实很好理解，正如我们在“流体的性质”一节中曾提到过的例子：如图5.4 所示，由于河水的黏性，靠近岸边的河水流速较小，水压较大；而河中央的河水流速较快，水压较小，并由此形成从河边指向河中央的水压。正是这个水压差，使在河中央游泳的人需要更大的力气才能游回岸边；也正是这个水压差，把在河边游泳或者溺水的人迅速推向河中央的危险地带。因此，我们需要尽量避免到水流湍急的河里尤其是到河中央游泳，以免造成溺水的危险。

图5.4　河水的黏性会导致流速差和压强差

伯努利所发现的“边界层表面效应”虽然没有给出完整的数学表达式，但它仍然很好地体现了：在等高定常流动条件下，流体的流速v 和压强p 之间具有“反向变化”的趋势（并非“反比例变化”），堪称“伯努利方程”的逻辑雏形。因此，这个效应也被人们称为“伯努利效应”，其实质是“伯努利方程”的一个“等高推论”，用数学表达式可以写为：

根据“伯努利效应”的结论，我们可以轻松地解释生活中一些常见的物理现象，也有很多有趣的实际应用。比如：当我们把一张小纸条贴着下嘴唇，从纸条上方用力吹气时，会看到纸条向上飘起。这是因为吹气时，纸条上方具有较大的空气流速，根据“伯努利效应”可知：纸条上方具有较小的气压，而纸条下方由于空气静止而具有较大的气压，所以纸条会在气压差的作用下向上飘起，并在气流的作用下剧烈抖动。千万不要小看了这个压强差，它不仅能使纸条飘起，如果吹气的角度和力量合适，它甚至还能使沉重的金属硬币飞起（请参考本书配套慕课视频）。而在“伯努利效应”的启发下，聪明的读者还可以用嘴吹气来玩“硬币乒乓球”的游戏。在用勺子调咖啡的过程中，我们常常会看到：咖啡杯中间也就是有“漩涡”的液面会向内凹陷，而四周的液面则相对较高。其实，咖啡液面的这种差异也与“伯努利效应”有关。原来，勺子的搅动会带动咖啡做自旋运动，又由于咖啡的黏性，杯子中间部分的咖啡流速要大于靠近杯壁的部分，所以中间的液压较小，会在大气压的作用下向内凹陷。

龙卷风是一种恶劣的自然灾害，在龙卷风来临时，地面上几乎所有的物体，包括人、牲畜甚至是沉重的汽车，都可能被卷上天空。在与龙卷风斗争的漫长过程中，人们逐渐发现龙卷风有一个特殊的爱好，虽然难以卷走整栋建筑，但龙卷风却常常喜欢把屋顶掀翻。这真是奇怪的事情，难道龙卷风和屋顶之间有什么“私人恩怨”吗？其实，这个现象可以用“伯努利效应”来做出很好的解释：在风和日丽的天气时，屋顶上下空气静止，都是标准大气压；但在刮龙卷风时，由于屋顶上方的空气流速极大，气压极小，而封闭的屋内由于空气流速很小而仍然保持较大的气压。正是由于屋顶上下的气压差作用，屋顶才会被屋内的强气压掀开，并被龙卷风卷走，这就是龙卷风与屋顶之间的秘密。显而易见，在龙卷风灾害发生时，如果我们想要尽量保护房屋结构完整，恐怕打开门窗会是相对较好的选择。(www.xing528.com)

在固定翼飞机的设计中，工程师则根据“伯努利效应”设计了特殊的机翼，并在飞机起飞和飞行的过程中起到了非常重要的作用。固定翼飞机的机翼通常具有弧形上沿，当飞机高速滑行时，从弧形机翼上方流过的空气由于“具有相对较远的距离”（相同的时间内要通过更远的距离），会具有较大的流速和较小的气压，而机翼下方的气压较大，这将使机翼通过压强差获得向上的升力；然后，飞机头部再适当扬起，气流在斜向下运动的同时，给飞机一个斜向上的反作用力（请参考本书配套慕课视频）。就这样，在“伯努利效应”和“牛顿第三定律”的共同作用下，飞机飞起来了。不仅是空中的飞机，地面上一些跑车也常常被设计成所谓的“流线形”，也就是上部呈光滑的圆弧状。这样一来，当“流线形”汽车启动后，会受到较大的升力作用，从而减小车轮与地面的摩擦阻力，促使汽车跑出更快的速度。

除了为飞机和跑车提供升力，“伯努利效应”还会呈现出神秘的吸引力。比如，我们打开一个吹风机，并让风竖直向上吹，同时在气流中轻轻放置一个乒乓球（请参考本书配套慕课视频）。这时，我们会看到：乒乓球不但没有被气流吹走，反而好像被一种神秘的力量吸住了一样，只能在气流中上下波动；当我们把吹风机在水平面上缓慢移动时，乒乓球也会相应地移动，并不会脱离气流。这是因为：吹风机吹出的气流速度很大，所以气流中心的气压很小；相反，气流外侧的流速较小，气压较大。所以，当乒乓球偏离气流时，就会在外界较大的气压作用下压回气流中，并由于气流支持力和自身重力的平衡而“悬浮”在气流中。

在足球比赛中，一些球星比如梅西和C罗，常常能踢出飞行轨迹呈弧线的“香蕉球”或者“电梯球”，让对方守门员一筹莫展的同时，拯救自己的球迷和球队。其实，踢出弧线球的关键在于制造旋转，运动员一般通过脚内侧或者外侧触球，在使足球向前飞行的同时产生剧烈的旋转，并最终划出一道“美妙的弧线”。如图5.5 所示，在1997 年的“法国杯”巴西对阵法国的足球赛中，当时巴西队获得一个距离球门正前方40米外的任意球，巴西队边后卫卡洛斯助跑后用左脚外脚背大力抽射，人们眼看着足球飞向角旗，但很快又划出一道夸张的曲线折回并命中球门右上方的死角，而法国队门将巴特兹没能做出任何反应。卡洛斯的这个进球直到如今仍然被很多资深球迷认为是人类足球史上的最佳任意球，但是就连卡洛斯本人也说不清为什么会有这样的效果，那么卡洛斯究竟是怎么做到的呢？原来，卡洛斯是用左脚外脚背大力抽射的，这使得足球在朝角旗方向高速飞行的同时还会做逆时针旋转。在这里，我们要考虑足球与空气的相对流向：首先，如果把向前飞行的足球看成相对静止，那么原本静止的空气则可以看成在足球两侧相对向后运动。值得注意的是：此时，粗糙的球皮也会带动部分靠近球表面的空气分子向前运动，但与相对向后运动的空气相比，向前运动的空气分子太少了，根本无法扭转空气整体向后运动的大趋势，所以可以忽略；其次，足球还在做逆时针旋转，所以足球左侧会向后运动，由于球皮粗糙会带动部分表面空气分子也向后运动，与空气整体流动方向一致，所以这会导致左侧有较大的空气相对流速；相反，足球右侧的球皮则会带动表面空气分子向前运动，与空气整体流动方向相反，并因此减小右侧的空气相对流速。虽然左右两侧球皮所带动的表面空气很少，但这仍然会导致足球左右两侧的空气流速产生些许差异，并形成流速左快右慢、压强左小右大的情况，从而使足球的飞行线路向左发生偏折，呈现出弧线球的轨迹。不过，这个任意球的旋转弧度是如此惊世骇俗，还在于卡洛斯的抽射力量十足，使球的旋转速度极快，所以才能产生了这样的“超级大回旋”。当然，法国杯的比赛用球也助了卡洛斯一臂之力，因为这个球采用了新型复合泡沫材料，内部结构是排列紧密的弹性气泡，这使得足球表面更具耐磨性和摩擦性，从而更容易制造旋转。

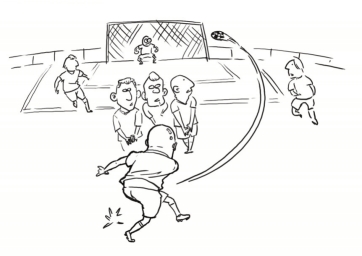
图5.5　足球比赛中的伯努利效应

有时，在一些较为复杂的例子中，我们可能需要同时应用理想流体的“连续性方程”和“伯努利效应”进行分析。比如，我们将一个乒乓球放到玻璃漏斗的宽口面内，然后从漏斗的窄口竖直向下吹气，就会看到一个“反重力”的奇怪景象（请参考本书配套慕课视频）：漏斗里的乒乓球就像被吸住了一样，虽然在漏斗中剧烈颤动，但就是掉不下来。乍一看，这个现象十分难以理解，因为乒乓球本身受到向下的重力，同时还会受到从上向下的吹气冲力，可乒乓球怎么就掉不下来呢？究竟是什么样的神秘力量在支持漏斗里的乒乓球呢？其实，这个现象的理解就需要同时应用到“连续性方程”和“伯努利效应”。首先，漏斗窄口的面积较小，而宽口的面积较大，根据“连续性方程”的结论，窄口的气流流速较大，而宽口的气流流速较小。再根据“伯努利效应”可知，上方的窄口流速大而气压小，下方的宽口流速小而气压大，所以乒乓球才会在窄口和宽口的“气压差”作用下保持不落下。