下一代二维生物的几何学知识

下面一个例子比下落的升降机的例子还要奇特。我们必须接触到一个新的问题：广义相对论与几何学之间的关系。我们先来描述一个另外的世界，在那里面生存着二维的生物，而不是像我们的世界里那样生存着三维的生物。电影已经使我们习惯于感受在二维银幕上演出的二维生物。我们现在设想银幕上的这些影子（出场人物）是实际存在的，他们有思维的能力，能创造他们自己的科学，二维的银幕就是他们的几何空间。这些生物不能具体地想象一个三维空间，正如我们不能想象一个四维世界一样。他们能够折转一根直线，知道圆是什么，但是不能做一个球，因为这就等于丢弃了他们的二维银幕。我们的处境也与之类似。我们能够把线和面折转和弯曲过来，但是我们很难想象一个折转或弯曲的三维空间。

这些影子通过生活、思维和实验，最后可以精通二维欧几里得几何学的知识。因此，他们能证明三角形的内角之和为180°。他们能够做出有公共圆心的一大一小的两个圆。他们会发现，两个这样的圆的圆周之比等于它们的半径之比，这种结果正是欧几里得几何学的特征。如果银幕无限大，这些影子会发现，若笔直往前旅行，他们永远也不会回到起点。

现在，我们想象这些二维生物的环境改变了。我们再想象有人从外面，即从“第三维”，把他们从银幕上迁移到具有很大半径的圆球上。假如这些影子比起全部球面来是极小的，假如他们无法做遥远的通信，又不能走动得很远，则他们不会感觉到有什么变化。小三角形的内角之和仍是180°。具有共同圆心的两个小圆，其半径之比仍等于其周长之比。他们沿着直线旅行，还是不会回到他们的起点。

但是假设这些影子慢慢发展起他们的理论和技术知识。假使他们有了交通工具，能够很快地通过巨大的距离，他们便会发现，笔直往前旅行，最后还会回到他们的起点。“笔直往前”就是沿着圆球的巨大圆周走去。他们也会发现，具有公共中心的两个圆，假如一个半径很小，另一个很大，则其周长之比不等于其半径之比。

假如我们的二维生物是保守的，假如他们在过去几代所学的都是欧几里得几何学，那时候他们不能往远处旅行，那时候这种几何学跟观察到的情况是相符的，那么，尽管他们在测量上有明显的误差，他们也必然要尽可能去维护这种几何学。他们力求使物理学来挑起这些矛盾的重担。他们想寻找一些物理学上的理由，例如温度之差来解释线的变形，说这种变形使测量结果与欧几里得几何学不符了。但是他们迟早总会发现，有一种更合理、更确切的方法来描写这些现象。他们最后会懂得他们的世界是有限的，还有跟他们所学的有很大不同的几何学原理。他们即使没有能力想象这些原理，也会知道，他们的世界是一个圆球上的二维表面。他们将很快地去学新的几何学原理，这些原理虽与欧几里得的不同，但是对他们的二维世界仍然是一致的、合乎逻辑的。下一代的二维生物便学到圆球的几何学知识，他们会觉得旧的欧几里得几何学似乎更复杂和牵强，因为它与观察到的情况不符。

我们再回到我们的世界中的三维生物上来。

说我们的三维空间具有欧几里得性，这是什么意思呢？这句话的意思是说所有欧几里得几何学中理论上证明了的命题，都能够用实际的实验加以证明。我们能够利用坚硬的物体或光线做出符合欧几里得几何学中的理想形体的实际形体。一把尺的边缘或一束光相当于一条线。用很细的坚硬的杆所构成的三角形的内角之和等于180°。用两根很细的弹性金属线所构成的同心圆的半径之比等于其周长之比。欧几里得几何学用这个方式来解释以后，便成了物理学的一章，不过这是很简单的一章。

但是我们可以认为矛盾已经找到了：例如由杆（有许多理由都认为它们是坚硬的）构成的大三角的内角之和不再等于180°了。因为我们已经习惯于用坚硬的物体来具体表示欧几里得几何学的观念，那么我们也许要寻找一些物理的力来解释我们的杆的这种意料不到的变形。我们力求发现这种力的物理性质，以及它对其他现象的影响。要挽救欧几里得几何学，我们会归罪于实际形体的不坚硬，会归罪于实际形体与欧几里得几何学中的形体不完全相符。我们要设法寻找一种更好的物体，它表现得和欧几里得几何学所期望的完全一致。可是，假如我们不能把欧几里得几何学和物理学结合成一个简单一致的图景，那么我们必须放弃关于我们的空间是欧几里得性的观念，并且要将我们的空间的几何性质做更普遍的假设，以便寻求更确切的“实在”的图景。

这个必要性可以用一个理想实验加以说明。这个实验告诉我们，一个真正的相对论物理学不能建筑在欧几里得几何学的基础上。我们的论证要引用我们已经知道的惯性坐标系和狭义相对论的结果。

设想一个大圆盘，上面画着两个同心圆；一个很小，另一个非常大。圆盘很快地旋转。圆盘是相对于外面的观察者转动的，假设圆盘里面还有一个观察者。我们再假定外面的观察者的坐标系是惯性的。外面的观察者也可以在他的惯性坐标系中画出同样一大一小的两个圆，这两个圆在他的坐标系中是静止的，但与圆盘上的圆相重合。他的坐标系是惯性的，因此欧几里得几何学在他的坐标系中是有效的，他会发现两圆周之比等于其半径之比。但是在圆盘上的观察者又发现了什么呢？从经典物理学和狭义相对论的观点看来，他的坐标系是被禁用的。但是假如我们想为物理学定律找出能适用于任何坐标系的新形式，那么我们必须以同样严肃的态度来对待圆盘上和圆盘外的观察者。现在我们是从外面来注视圆盘里面的观察者，看他如何靠测量去寻找旋转的盘上的周长与半径。他所用的小尺，与外面的观察者所用的是一样的。所谓“一样的”，是指实实在在一样的，就是说它是由外面的观察者交给里面的观察者的，或者说，它是在一个静止的坐标系中长度相同的两把尺中的一把。

图65

里面的观察者在盘上开始测量小圆的半径与周长。他的结果一定与外面的观察者的完全一样。圆盘围绕着它旋转的轴通过圆盘的中心。圆盘上接近于中心的那些部分的速度非常小。如果圆足够小，那么我们完全可以放心地使用经典物理学而不必顾及狭义相对论。这就是说，对于里面的和外面的观察者来说，尺的长度是一样的，因而对这两个观察者来说，两种测量的结果是一样的。现在盘上的观察者又来测量大圆的半径。放在半径上的尺相对于外面的观察者是在运动的。但是因为运动的方向跟尺垂直，这样尺是不收缩的，因而对两个观察者来说，它的长度是一样的。这样，对这两个观察者来说，三种测量结果是相同的：两个半径和一个小圆的圆周。但是第四种测量则不然。两个观察者所测的大圆的周长是不相同的，放在圆周上的尺朝着运动的方向，因此依照外面的观察者的观测，比起他的静止的尺来，现在它显得收缩了。外圆的速度较内圆的大得多，因而必须计及这种收缩。因此如果应用狭义相对论的结果，我们的结论应该是这样的：两个测量者所测量的大圆的周长一定是不同的。由于两个观察者所测量的四种长度中只有一种是互不相同的，因此里面的观察者不能和外面的观察者一样认为两半径之比等于两圆周之比。这就是说，在盘上的观察者不可能在他的坐标系中确认欧几里得几何学的有效性。

圆盘上的观察者得到这种结果以后，还可以说他不想去考察不能应用欧几里得几何学的坐标系。欧几里得几何学之所以崩溃，是因为绝对转动，是因为他的坐标系是坏的和被禁止的。但是在这个论证中，他已经拒绝了广义相对论中的主要观念。另一方面，如果我们拒绝绝对运动的观念而保持广义相对论的观念，那么物理学就必须建立在比欧几里得几何学更普遍的一种几何学的基础上。假如所有的坐标系都是可以允许的，便无法逃避这个结局。

广义相对论所引起的变化，不能只局限于空间一方面。在狭义相对论中静止在一个坐标系中的许多钟，步调相同而且是同步的，就是说同时指示相同的时刻。在一个非惯性的坐标系中的钟会怎样呢？前面的圆盘的理想实验又用得着了。外面的观察者在他的惯性坐标系中有步调完全相同，并且是同步的许多完好的钟。里面的观察者从这同类的钟里拿出两只，一只放在小的内圆上，另一只放在大的外圆上。内圆上的钟，相对于外面的观察者以很小的速度在运动。因此我们可以放心地断定，它的步调和圆盘以外的钟相同。但是大圆上的钟有很大的速度，和外面观察者的钟比较起来，步调变了，因此和放在小圆上的钟比较起来，步调也变了。因此，两只旋转的钟就有了不同的步调，而且，应用狭义相对论的结果，又发现我们在旋转的坐标系中不能把钟安置得和惯性坐标系中所安置的那样。

为了使我们可以明白从这个理想实验中和前面所描写的理想实验中究竟能够得出怎样的结论，不妨再引用信奉经典物理学的老派物理学家（古）和懂得广义相对论的现代物理学家（今）之间的一次对话。老派物理学家是站在惯性坐标系中的外面的观察者，而现代物理学家站在旋转的圆盘上。

古：在您的坐标系中，欧几里得几何学是无效的。我观察了您的测量，我承认在您的坐标系中，两个圆周之比不等于两个半径之比。这正表示您的坐标系是被禁用的。可是我的坐标系是惯性的，我能够放心地应用欧几里得几何学。您的圆盘在做绝对运动，而根据经典物理学的观点，它是一个被禁用的坐标系，在它里面，力学定律是无效的。(www.xing528.com)

今：我不愿意听取任何关于绝对运动的说法。我的坐标系和您的一样好。我看见您对我的圆盘在旋转。没有人能够禁止我把一切运动都关联于我的圆盘。

古：但是您不觉得有一种奇怪的力使您离开圆盘的中央吗？假如您的圆盘不是一个很快地旋转着的旋转木马，那么您所观察到的两种情况一定不会发生。您不会注意到有一种力把您推向盘的边缘，也不会注意到欧几里得几何学在您的坐标系中是不能应用的。难道这些论据都不足以使您相信您的坐标系是在做绝对运动吗？

今：一点也不！我自然注意到您所说的两种情况，但是我认定它们都是由于作用于我的圆盘上的引力场所引起的。从圆心指向圆盘外面的引力场，使我的坚硬的杆变形，使我的钟改变步调。引力场、非欧几何、步调不同的钟，在我看来都是密切相关的。不管采用哪一种坐标系，我必须同时认定相应的引力场的存在以及它对坚硬的杆和钟的影响。

古：但是您知道您的广义相对论所引起的困难吗？我想用一个简单的不属于物理学范围的例子来说清楚我的观点。设想一个理想的美洲式城市，它是由一些平行的南北大街和平行的东西大道组成的。大街与大道相互垂直；大街与大街之间，大道与大道之间的距离是一样的。如果这一假定被满足，则由街道围成的每一个区域的大小都是一样的。用这种方法，我可以很容易地表示出任何一区的位置。但是如果没有欧几里得几何学，这样一种构图法是不可能的。然而我们不可能把我们的整个地球用一个很大的理想的美洲式城市包盖起来。看一眼地球仪，您就相信这一句话了。但是我们也不能把您的圆盘用这样一种“美洲式城市结构”包盖起来。您说您的杆已经由于引力场的作用而变形了。您既然不能证明关于半径和圆周之比相等的欧几里得定理，这就清楚地表明如果您把这种街道结构延伸到很远的地方，迟早会发生困难，而发现在您的圆盘上这样构图是不可能的。您的圆盘上的几何图形很像曲面上的几何图形，而在很大面积的一块曲面上，这样的街道图自然是不可能的。再举一个更带物理性质的例子。取一个平面，这个平面的各个不同部分不规则地加热到不同的温度。您能够用受热便会在长度上膨胀的小铁条，画出图66所画的那种“平行—垂直”图吗？自然不能！您的引力场对您的杆所起的作用，正和温度的改变对小铁条所起的作用是一样的。

今：所有这些都不能把我难倒。街道图是用来决定一个点的位置的，而钟是用来决定事件的次序的。但是城市不一定必须是美洲式的，它也完全可以是古欧洲式的。设想您的理想城市是由塑性材料造成的，造成后再使它变形。虽然街道已经不是笔直的、等距的了，但是我还可以数出街区并认清街道。同样，在地球上虽然不是“美洲式城市”的街道图形，但是我们也能用经纬度来指示点的位置。

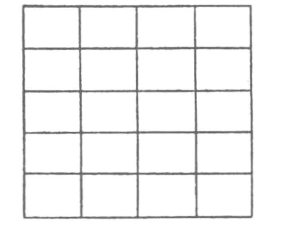
图66

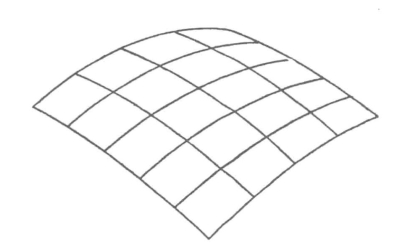
图67

古：但是我还是看到一个困难。您被迫使用您的“欧洲式的城市图”。我承认您能建立起事件或点的次序，但是这种作图法会使一切关于距离的测量混乱不清。它不能像我的作图法那样给您空间的度量性质。举例来说，我知道在我的美洲式城市中，走过十个街区所经过的距离是走过五个街区的两倍。因为我知道所有的街区是相等的，所以能够立刻决定距离。

今：这些话都对。在我的“欧洲式城市图”中，我不能够立刻用变了形的街区的数目来决定距离。我必须知道更多的知识，我必须知道我的城市图的表面的几何性质。正如每个人都知道的，赤道上自经度0°至10°的距离，与北极附近同样自经度0°至10°的距离是不相等的。但是每个领航员都知道如何决定地球上这样两点之间的距离，因为他知道地球的几何性质。他或者根据球面三角学的知识来计算，或者用实验方法让船以同样的速度驶过这两段距离来计算。在您的情况中，整个问题是无关紧要的，因为所有的大街与大道之间的距离都是相等的。在地球的情况中，要复杂得多；0°与10°的两根经线在地球的两极处相遇，而在赤道上相距最远。在我的“欧洲式城市图”中也是一样，我必须比您在您的“美洲式城市图”中多知道一些知识，然后才能决定距离。我可以在每种特殊情况中研究我的连续区的几何性质，以得到这种知识。

古：但是这一切都不过表示放弃欧几里得几何学的简单结构而换上您那下定决心去使用的复杂的框架是如何不方便罢了。难道这是必需的吗？

今：我想是的，假如我们想把我们的物理学应用到任何坐标系中去但没有神秘的惯性坐标系，我承认我的数学工具比您的更复杂，但是我的物理学上的假设却简单得多、真实得多。

这个讨论只限于二维连续区。在广义相对论中争论的问题更为复杂，因为那里不是二维连续区而是四维时—空连续区。但是观念还是和描写二维空间的一样。在广义相对论中，我们不能像在狭义相对论中那样来应用平行与垂直的杆的力学框架和同步的钟。在任意一个坐标系中，我们不能像在狭义相对论的惯性坐标系中那样来用坚硬的杆和同快慢及同步的钟决定一个事件所发生的地点与时刻。我们仍然能够用非欧几里得的杆和快慢不齐的钟来确定事件。但是要用坚硬的杆和绝对同快慢与同步的钟来做的实际实验，只能在局部性的惯性坐标系中进行。在这种坐标系中，整个狭义相对论都是有效的。但是我们的“好的”坐标系只是局部性的，它的惯性是受空间和时间的限制的。甚至在任意的坐标系中，我们也能预知在局部性的惯性坐标系中所做的测量的结果。但是要做到这一点，我们必须知道我们的时—空连续区的几何性质。

我们的理想实验只指出新的相对论物理学的一般性质。这些实验告诉我们，基本的问题是引力问题。它们还告诉我们，广义相对论把时间和空间的概念进一步推广了。