我们的新假设是:
1.在所有相互做匀速直线运动的坐标系中,光在真空中的速度都是相同的。
2.在所有相互做匀速直线运动的坐标系中,自然定律都是相同的。
相对论就是以这两个假设为开端的。从现在起,我们不再运用经典转换了,因为我们知道它和这两个假设相矛盾。
在这里,跟科学工作中常常所做的一样,需要把自己根深蒂固的、常常未经评判便加以接受的偏见除掉。因为我们已经知道,如果把上节中的第一点和第二点加以改变,就会导致跟实验发生矛盾,所以我们必须有勇气坚定地承认它们是正确的,而攻击那可能攻得下的弱点,即位置与速度从一个坐标系转换到另一个坐标系中的方法。我们的意图是从第一点和第二点推出结论,研究一下这两个假设跟经典转换相矛盾的地方在哪里,是怎样矛盾的,并找出所得到的结果的物理意义。
我们再来利用房内房外有两个观察者的运动着的房间的例子。假设一个光的信号由房间的中央发射出去,我们再问这两个人,他们想观察什么,这时候他们只承认上面的两个原理,完全丢掉了以前说过的关于光穿过介质而传播的论据。我们把他们的回答引用如下:
里面的观察者:从房间中央发出的光的信号会同时到达房间的各个墙上,因为四扇墙与光源的距离相等,而光在各方向上的速度又是相等的。
外面的观察者:在我的坐标系中,光的速度与随着房间运动的观察者的坐标系中所看到的完全一样。在我的坐标系中,光源运动与否毫无关系,因为光源的运动并不影响光速。我所看到的只是光的信号同样以标准速率向各个方向行进。一扇墙要奔离光的信号,而另一扇墙要接近光的信号。因此信号到达那扇奔离的墙比到达那扇接近的墙要稍微迟一些。假使房间的速度比光速小很多,那么,虽然信号到达两扇墙的时间之差也会小很多,但信号绝不会完全同时到达与运动方向相垂直的两扇相对的墙。
比较这两个观察者的预言,我们会发现一个非常惊人的结果,这种结果显然跟经典物理学上极有根据的概念相矛盾。现在发生了两个事件,两束光到达两扇墙,在房内的观察者看来,它们是同时到达的,而房外的观察者却认为它们不是同时到达的。在经典物理学中,对在任何坐标系中的观察者来说,用的都是同一只钟,时间的流逝是一样的。因此,时间和“同时”“早些”“迟些”等词一样,都有一种与任何坐标系无关的绝对意义。在一个坐标系中同时的(即时间过程相同的)两件事,在任何其他坐标系中也必定是同时的。
上述两个假设,也就是相对论,使我们不得不放弃这种观点。我们已经描述过,在一个坐标系中同时的两个事件,在另一个坐标系中却不是同时的。我们的任务就是要了解这个结果,了解“在一个坐标系中同时的两个事件,在另一个坐标系中可能不是同时的”这句话的意义。
“在一个坐标系中同时的两个事件”表示什么意思呢?每个人在直觉上似乎都知道这句话的意思。但是我们的见解必须谨慎些,并力求做出严格的定义,因为我们知道太重视直觉实在太危险。我们首先来回答这个简单的问题。
一只钟究竟是什么呢?
时间流逝的原始的、主观的感觉使我们能够排列出印象的次序,以断定这件事发生得早些,那件事发生得迟些。但是要表示两个事件之间的时间间隔为十秒钟,就需要一只钟。由于使用了一只钟,时间的概念就变成客观的了。任何物理现象,只要它能够照原样重复任意次,都可以被当作一只钟。如果我们取这个现象的首尾之间的时间作为时间的单位,那么重复这个过程就可以测定任何时间间隔。所有的钟,从最简单的沙漏到最精密的仪器,都是以这个观念为基础的。例如使用沙漏的时间单位便是沙由上面的玻璃瓶流到下面的玻璃瓶的时间间隔,把玻璃瓶倒转过来就可以重复这个物理过程。
在两个离得很远的点上有两只完好无损的钟,它们上面所指示的时刻完全一样。不论我们用哪种方法来对这句话做出实验验证,它总应该是正确的。但是,它是在表示什么意思呢?我们怎样才能确信两只距离很远的钟所指示的时刻是完全一样的呢?一个可能的办法就是使用电视。必须了解,电视只用来作为一个例子,它在我们的论证中并不重要。我们可以站在一只钟的旁边而看着另一只钟在电视屏幕上的影像。于是我们可以判断它们是否显示着相同的时刻。但是这不会是一个好的证明。电视中的影像是由电磁波传递的,因此是以光速传播的。我们在电视屏幕上所看到的影像是在一个非常短的时间以前发出的,而我们在真实的钟上所见到的时刻却是现在发生的。这种困难很容易被避免。我们必须在这两只钟的距离的中点处摄取这两只钟的电视图,在这个中点上观察它们。如果信号是同时发出的,它们也同时到达中点处。假使从中点上所观察到的两只好钟一直指示相同的时间,那么它们便适宜于用来指示距离很远的两点上的时间。
在力学中,我们只用了一只钟。但这不是很方便,因为我们必须站在这只钟的附近进行所有的测量。假如从远处望钟,例如用电视的方法从远处望钟,我们必须时常记住:我们现在所看到的实在是过去发生的,正如在看日落时,我们是在日落发生的8分钟以后才看到的。我们读记下来的时刻都必须根据我们与钟的距离做相应的修正。
因此,只有一只钟是不方便的。但是现在我们既已知道怎样判断两只或者更多只钟是否同时指示一个时刻,是否走得一样,便很容易想象在给定的坐标系中可以随我们的意思设置多少只钟。其中每一只都可以帮助我们决定它的近旁所发生的事件的时间。所有这些钟相对于坐标系都是静止的。它们都是“好”钟;它们都是同步的,就是说在同一时间显示相同的时刻。
关于钟的这样布置并不是一件特别奇怪的事情。我们现在用很多只同步的钟来代替从前的只用一只,因此很容易判断在给定坐标系中,两个相距遥远的事件是否同时发生。假使两个事件发生时,它们附近的同步的钟都指示出同样的时刻,它们便是同时的。两个相距很远的事件中的一个比另一个发生得早些的说法现在就有了确定的意义。这种情况都可以用静止在我们的坐标系中的同步钟来判断。
所有这些都是跟经典物理学一致的,也没有一点跟经典转换相矛盾的地方。
为了确定同时的事件,利用信号来使钟同步。在我们的布置中,重要的一点是,信号是以光速传播的,光速在相对论中担负着极为重要的任务。
因为我们要讨论两个相对做匀速直线运动的坐标系的重要问题,我们必须考察两根杆,每根杆上装有一些钟。这两个坐标系相对做匀速直线运动,在每个坐标系上的观察者现在都有了他自己的标尺和装牢在标尺上的一组钟。
在以前用经典力学讨论测量时,针对所有的坐标系,我们只用一只钟。现在我们在每一个坐标系中却用上了许多只钟。这个区别并没有什么重要意义。一只钟就够了,但是只要它们是很好的同步的钟,绝没有人反对用很多只钟。
现在我们接近指出经典转换跟相对论矛盾的主要观点上了。假如两组钟相对做匀速直线运动,结果会发生什么呢?持有经典观点的物理学家回答说:没有什么;它们还会走得一样快,因而我们既可以用运动的钟,也可以用静止的钟来指示时间。按照经典物理学,两个事件在一个坐标系中是同时的,在任何其他的坐标系中也是同时的。
但是,这不是唯一可能的答案。我们同样可以想象一只在运动中的钟跟一只静止着的钟,其机械运转的步调(走的快慢)是不同的。我们现在来研究这种可能性,暂时不必确定钟在运动时是否真会改变其步调。说一只运动的钟会改变步调是什么意思呢?为简单起见,我们假定在上面的坐标系中只有一只钟,而在下面的坐标系中有许多只。所有的钟的机构都相同,而下面的几只钟是同步的,就是说它们同时指示相同的时刻。我们把相对运动的两个坐标系的三个接连发生的位置表示在图55中,在第一图中,上面一只和下面三只钟的指针位置照例是一样的,因为我们原来是这样安排的。在第二图中,我们看到两个坐标系在过了一段时间以后的相对位置。所有在下面的坐标系中的钟都指示着相同的时刻,但是在上面的坐标系中,钟的步调却变了。由于这只钟是相对于下面的坐标系在运动,所以它的步调变了,时间不同了。在第三图中,我们看到钟的指针位置的差异随时间而增大了。
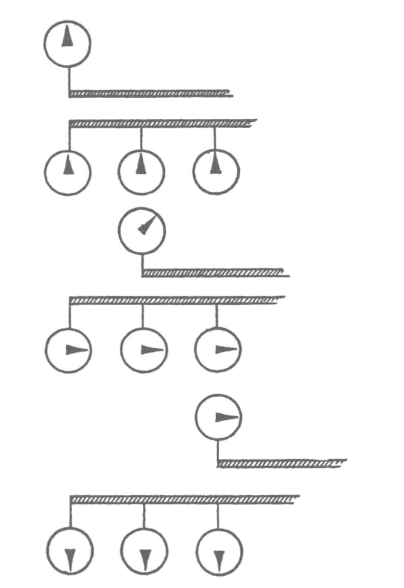
图55
一个静止在下面的坐标系中的观察者会发现一只运动的钟会变更它的步调。自然,如果钟相对静止在上面坐标系中的观察者而运动,也会发现同样的结果;在这种情形中,上面的坐标系中要有许多只钟,而下面的坐标系中却只要一只钟。在两个相对运动的坐标系中的自然定律必定是相同的。
在经典力学中,我们默认了一只运动的钟不会改变步调。这似乎太明白了,简直不值得再提起它。但是没有什么事情是显而易见的;假如我们要做得认真些、谨慎些,那么必须分析物理学中迄今被认为是理所当然的假设。
我们不能够仅因为一个假设跟经典物理学中的假设不同就认为它是不合理的。我们可以很容易地想象一只运动的钟会改变它的步调,只要这种改变的规律对所有的惯性系都是相同的。(https://www.xing528.com)
再举一个例子。试取一根米尺,这意味着它静止在一个坐标系中时长为1米。现在让它做匀速直线运动,在代表坐标系的杆上滑过。它的长度还会是1米吗?我们必须预先知道怎样去决定它的长度。当杆是静止的时候,它的两端跟坐标系上相隔1米的两个刻度重合。由此我们断定:静止的杆的长度等于1米。当尺在运动时,我们又怎样测量它的长度呢?可以用下面的方法进行。在给定时刻,两个观察者同时拍快照,一个拍运动的尺的始端,一个拍末端。由于照片是同时拍摄的,我们可以把尺的始端和末端跟坐标系重合的那个刻度比较。用这种办法,我们就可以决定它的长度。两个观察者必须在给定坐标系的不同部位观察同时产生的现象。我们没有任何理由认为这样的测量结果会跟尺在静止时的结果相同。因为照片必须是同时拍摄的,所谓同时,我们已经知道是与坐标系有关的一个相对的概念,因此在互做相对运动的不同的坐标系中,这种测量似乎很可能得出不同的结果。
我们很能想象,如果改变的规律对所有的惯性坐标系都是相同的,那么不仅运动的钟会改变它的步调,一根运动的尺也会改变它的长度。
我们只讨论了几种新的可能性,但都没有做出认定这些可能性的任何证明。
我们记得在所有的惯性坐标系中,光速都是一样的。这一情况跟经典转换是不相符的。闷葫芦必须在某处被打开。难道就在这里吗?我们难道不能假定运动的钟的步调和运动的杆的长度会改变,而由这些假定便直接推出光速的不变性吗?我们是能够的!这就是相对论和经典物理学根本不同的第一个例子。我们的论证可以倒过来说:假如光速在所有的坐标系中都是一样的,则运动的杆必须改变其长度,运动的钟必须改变其步调,掌握这些改变的定律就被严格地确定出来了。
这一切都没有什么神秘和不合理的地方。在经典物理学中,总是假定运动的钟和静止的钟都有相同的步调,假定运动的杆和静止的杆都有相同的长度,假如在所有的坐标系中光速都是相等的,假如相对论是有效的,那么我们必须牺牲这个假定。这些根深蒂固的偏见是很难被消除的,但是除此以外别无他法。从相对论的观点看来,旧概念似乎是很武断的。为什么要像前几页中所说的那样,相信对于所有坐标系中的一切观察者都是以同样的方式流逝的那种绝对时间呢?为什么要相信距离是不可能变的呢?时间是由钟决定的,空间坐标是由杆决定的,而决定的结果很可能与钟及杆在运动时的行为有关。我们没有理由相信它们的行为会依照我们所希望的方式来做。通过电磁场现象的观察间接地指出,一只运动的钟会改变它的步调,一根运动的杆会改变它的长度,而在力学现象中,我们不会想到会有这种情况发生。我们必须接受每个坐标系中的相对时间的概念,因为这是解决困难最好的出路。从相对论中发展出来的另外的科学成就表明,不应当把这个新的概念看作不得已才接受的东西,因为这个理论的功绩是非常显著的。
到目前为止,我们只是力求说明什么东西使我们做出相对论的基本假设,以及相对论如何迫使我们重新研究和修改经典转换,并用新的概念来对待时间和空间。我们的目的是要指出作为新的物理学和哲学观点的基础的观念。这些观念都是简单的,但是在这里已经提出的形式中,它们还不足以得出任何结论,不仅定量的结论得不到,定性的结论也得不到。我们必须再用那些老方法,即只解释主要观念,而不加证明地陈述其他一些观念。
为了弄清楚相信经典转换的古代物理学家(称之为古)和相信相对论的现代物理学家(称之为今)在观点上的区别,我们设想他们之间进行了下面的对话:
古:我相信力学中的伽利略相对性原理。因为我知道在两个相对做匀速直线运动的坐标系中,力学定律是相同的。或者换句话说,按照经典转换,这些定律是不变的。
今:但是相对性原理必须应用于我们外界的一切现象。在相对做匀速直线运动的坐标系中,不仅力学定律相同,所有的自然定律都必须是相同的。
古:但是在相对运动的坐标系中,所有的自然定律怎么能相同呢?场方程(即麦克斯韦方程)对于经典转换不是不变的。这是由光速的例子中可以明白看出来的。依照经典转换,这个速度在两个相对运动的坐标系中并不是一样的。
今:这只表明经典转换是不能应用的,因而这两个坐标系之间必须有一种与经典转换不同的关系,而且我们不能像这个转换定律中所做的那样,把不同坐标系中的坐标和速度联系起来。我们必须代之以新的定律,并从相对论的基本假设中把它们推导出来。我们暂且不管这个新转换定律的数学表示,只要知道它与经典转换不同就够了。我们把它称为洛仑兹转换(Lorentz Transformation)。可以证明,麦克斯韦方程组(场的定律)对于洛仑兹转换是不变的,正如力学定律对于经典转换是不变的。我们来回忆一下经典物理学中的情况:坐标有坐标的转换定律,速度也有速度的转换定律,但是两个相对做匀速直线运动的坐标系中的力学定律却是相同的。空间有空间的转换定律,但是时间却没有转换定律,因为时间在所有的坐标系中都是相同的。可是,在相对论中却不同了。对于空间、时间和速度都有跟经典转换不同的转换定律。但是自然定律在所有相对做匀速直线运动的坐标系中又必须是相同的。自然定律必须是不变的,但是不是像前面那样对于经典转换,而是对于新型的转换,即所谓洛仑兹转换是不变的。自然定律在所有的惯性坐标系中都是同样有效的,而且从一个坐标系转换到另一个坐标系是用洛仑兹转换来表示的。
古:我相信你的话,但我很想知道经典转换和洛仑兹转换的差别。
今:你的问题最好照下面的方式来回答。你且说出一些经典转换的特色,然后让我来解释一下它们是否已保存在洛仑兹转换中,倘若没有,再解释它们为什么改变了。
古:假如在我的坐标系中有一个事件发生于某一地点某一时刻,则在另一个相对于我的坐标系做匀速直线运动的坐标系中的观察者,对于这个事件发生的位置会选用不同的数,但是时间当然还是相同的。在所有的坐标系中,我们只用同一只钟,因此与钟是否运动毫无关系。在你看来也是对的吗?
今:不,不对。每个坐标系必须配备有专用的钟,这只钟必须是静止的,因为运动会改变钟的步调。在两个不同的坐标系中的两个观察者,不仅会用不同的数来确定位置,而且会用不同的数来确定这个事件所发生的时刻。
古:这表示时间不再是不变的。在经典转换中,所有坐标系中的时间总是相同的。在洛仑兹转换中,时间是变化的,并且变得和经典转换中的坐标有点相似。我奇怪,对于长度又能怎样呢?根据经典转换,一根坚硬的杆无论在静止中或运动中都保持它的长度不变。现在这还对吗?
今:不对了。根据洛仑兹转换,一根运动的杆在运动的方向上会收缩,而且假如速率增加,收缩也会增加。一根杆运动得愈快,便显得愈短。但是,这种收缩只发生在运动的方向上,在图56中,你可以看到一根杆运动的速度接近于光速的90%时,它的长度会缩到原来的一半,但在垂直于运动的方向上却没有收缩(图57)。

图56
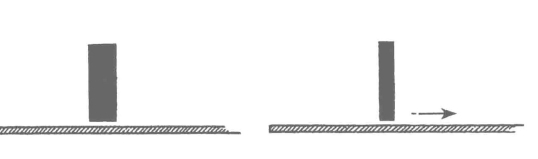
图57
古:这表示一只运动的钟的步调和一根运动的杆的长度都与速度有关。但它们的关系怎样呢?
今:速度愈增加,这种改变愈明显。根据洛仑兹转换,假如一根杆的速度等于光速,则它的长度会整个缩完。同样,与它所沿着经过的杆上的钟相比,一只运动的钟的步调会逐渐慢下来;如果它以光速运动,那么它就会完全停止。
古:这似乎跟我们所有的经验都不相符。我们知道一辆汽车不会在运动的时候就短一些。我们也知道汽车司机常常可以拿他的“好”的钟和他所经过的路上的钟加以比较,而发现它们总是完全一致的。这就跟你的说法不同了。
今:这一点当然是对的。但是在力学中,所有这些速度与光速相比都小得很,因此把相对论应用到这些现象上是荒谬的。每个司机即使把速率增加几十万倍,也还能泰然地应用经典物理学,只有当速度接近光速时,才能期望实验与经典转换之间有不相符的地方。只有在速度很大时,才能检验洛仑兹转换的有效性。
古:但是还有另外一个困难。根据力学,我可以想象物体的速度甚至比光速更大。一个物体相对于移动的船以光速运动,则它相对于岸的速度应当比光速更大。当一根杆的速度等于光速时,它的长度便整个缩完,这样会发生什么情况呢?如果杆的速度大于光速,我们不能期望有一种负的长度。
今:你实在没有理由做这样的讽刺!根据相对论的观点,一个物体不可能有比光速更大的速度。光速是所有物体所能具有的速度的最大限度。如果一个物体相对于船的速率等于光的速率,那么它相对于岸的速率也等于光的速率。将速度加上或减去的简单的力学定律在这里不再适用了。或者更确切地说,它对小的速度若不求精确还是可用的,但是对于接近光速的速度就不能应用。表示光速的数明显地出现在洛仑兹转换中,并且像经典力学中的无限大速度那样成为一个极限的情况。这个更为普遍的理论与经典转换和经典力学并不矛盾。反过来说,当速度在非常小的极限情况下,我们又回到旧概念上来了。从新理论的观点上可以明白地看出,经典物理学在哪些情况中是有效的,在哪些地方是受到限制的。在汽车、轮船和火车一类的运动中应用相对论,就像在只用乘法表便可以的地方却使用了计算机一样可笑。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




