物理学进化：力学框架及其重要性

在我们的故事说到这个阶段时，必须回溯到开始的地方——伽利略的惯性定律。我们再引用一次：

任何物体，只要没有外力改变它的状态，便会永远保持静止或匀速直线运动的状态。

一旦了解惯性的观念，似乎对于这个问题已经没有什么可说的了。虽然我们已经全面地讨论过这个问题，但是没有把它讨论彻底。

设想有一个很严格的科学家，他相信惯性定律可以用实际的实验加以证明或推翻。他在水平的桌面上推动小的圆球，并设法尽量消除摩擦。他注意到桌面与圆球愈加平滑，运动便愈加均匀。当他正要宣布惯性原理时，有人突然跟他开玩笑。这个物理学家是在一个没有窗户的房间里工作，并且与外界完全隔绝。开玩笑的人装置一种机械，可以使整个房间绕一根穿过它的中心的轴而旋转。旋转一开始，这个物理学家立刻得到新的、出乎意料的经验。原来是匀速直线地运动的圆球，现在尽量离开房间的中央而靠近房间的墙壁。他自己感到有一种奇怪的力把他推向墙去。他所体验到的感觉和在一个转急弯的火车或汽车中的人所感到的相似，和坐在旋转木马上所感到的更相似。他过去所得到的一切成果现在都被粉碎了。

这个物理学家若要放弃惯性定律，必须同时放弃所有的力学定律。惯性定律是他的出发点；假如这个出发点改变了，那么他的一切结论也都改变了。如果一个观察者毕生都是在一个转动的房间内度过的，并且在它里面进行各种实验，那么他所得到的物理学定律跟我们的是不同的。另一方面，如果他在进入房间以前对于物理学的原理已经有了很深的知识和坚定的信念，那么他就解释力学定律之所以被推翻，是因为房间在转动。用力学的实验，他甚至能测定它是怎样转动的。

我们为什么对这个旋转的房间内的观察者产生这么大的兴趣呢？道理很简单，因为在某种程度上，我们在地球上也是处于同样的地位。从哥白尼时代以来，我们便知道地球是绕着它自己的轴旋转并环绕着太阳运行的。在科学发展中，甚至这个任何人都很清楚的简单观念也不会不受触动。但是我们暂且抛开这个问题，接受哥白尼的观点。假使那个旋转着的观察者不能确认力学定律，那我们在地球上自然也不能确认它。但是地球转动得较慢，所以转动的影响不明显。可是有许多实验都证明跟力学定律有些偏差，这些实验的一致性可以被看作地球转动的证明。

可惜我们不能置身于太阳与地球之间，在那里去证明惯性定律的绝对有效性以及观察一下转动着的地球。这只有在想象中才做得到。我们所有的实验都只能在我们所居住的地球上进行。这句话常常被我们更科学地说成：我们的坐标系是地球。

我们不妨举一个简单的例子，把这句话的意思说得更清楚些。我们能够预言一个从塔上掷下来的石子在任何时刻的位置，并用观察来确认我们的预言。假使把一根量杆放在塔边，我们便可以预言在某个时候，落体会与杆上的一个数码相合。不言而喻，塔和量杆都不是用橡皮或其他在做实验时会发生变化的物质制成的。事实上，一根严密地跟地球相联系的刻度不变的尺和一只好的钟，这就是做实验时我们所需要的一切。我们只要有这两样东西，不仅可以不管塔的建筑怎样，甚至有没有塔都可以不管。上面所说的种种假定都是很平凡的，在描写这些实验时通常不会被提到。但是这个分析表明，在我们的每一句话后面都隐藏有许多假定。在这个例子中，我们假定有一根坚硬的量杆和一只理想的钟，若没有这两样东西，我们就不能检验伽利略的落体定律是否有效。用这样简单而重要的实际器具——一根量杆和一只钟，我们就能够以一定程度的准确性确认这个力学定律。如果这个实验做得非常仔细，它便会发现理论和实验之间有些不符，这种不符是由于地球的转动而产生的，或者换句话说，这是由于这里所表述的力学定律，在严密地跟地球相联系的坐标系中不是十分有效的。

在所有的力学实验中，不论是哪一种形式的实验，我们必须决定质点在某一确定时刻的位置，正如在上述实验中决定落体的位置一样。但是位置总是对于某种物件来说的，例如在上述的实验中，落体的位置是对于塔与刻度尺来说的。我们必须有一些所谓参考系，这是用来决定物体的位置的力学框架。例如在城市中，要决定物和人的位置，大街和小巷就是我们参考的框架。到目前为止，我们引用力学定律时都没有想过要说明所参考的框架，因为我们住在地球上，而在任何情况中都不难选择一个与地球严密地相联系的参考框架。我们把所有的观察都关联到它上面的这个参考框架是由坚硬不变的物体构成的，这个框架被称为坐标系。

我们所有的物理描述都还缺少某些东西。我们没有注意到任何观察都必须在一定的坐标系中进行。我们不去描写这个坐标系的结构，反而根本忽视它的存在。例如，过去我们写“一个物体匀速地在运动……”，其实我们应该这样写：“一个物体对某一选定的坐标系匀速地在运动……”那个关于旋转的房间的经验告诉我们，力学实验的结果可能跟我们所选定的坐标系有关。

假如两个坐标系相对转动，那么力学定律不能在两者之中都有效。如果把一个游泳池作为这两个坐标系中的一个，它的水面是平的，那么在另一个坐标系中，同样的游泳池里的水面就会是弯曲的，正如任何人用茶匙搅动杯中的咖啡那样。

在前面叙述力学的主要线索时，我们忽略了很重要的一点。我们没有说出它们在哪一种坐标系中是有效的。因此，全部经典力学就等于悬在半空中，因为我们不知道它属于哪一个坐标系。然而，让我们暂且不去管这个困难。我们来做一个不十分准确的假定，就是说认为在所有与地球严密地相联系的坐标系中，经典力学的定律都有效。这样做是为了把坐标系确定下来，使我们叙述起来可以明白一些。虽然我们说地球是一个适宜的参考坐标这句话并不十分正确，但我们暂且这样承认它。

因此，我们假定有一个坐标系；在这个坐标系中，力学定律是有效的。这样的坐标系只有一个吗？我们假设有一个像一列火车、一艘船、一架飞机那样的坐标系，它相对于地球在运动。在这些新的坐标系中，力学定律都有效吗？我们确实知道它们不是一直有效的，例如火车在转弯时，船在风暴中颠簸时，飞机在翻身时，它们就不再有效了。我们先说一个简单的例子。如果有一个坐标系匀速地相对于一个“好的”坐标系在运动，所谓一个“好的”坐标系就是力学定律在其中有效的坐标系。例如，沿着直线以不变的速率在行驶的一列理想火车或一艘航行得异常平稳的船。我们从日常的经验中得知这两个坐标系都是“好的”，因为在匀速直线地运动着的火车或轮船中所进行的物理实验和在地面上所做的结果完全一样。但是假如火车突然停止了，或急剧地加快了，或者海面突然起了风浪，便会发生异常的情况。在火车里，箱子从行李架上掉下来了；在船上，桌子和椅子翻倒了，乘客也晕船了。从物理学的观点看来，这只表示力学定律不能在这些坐标系中被应用，它们是“坏的”坐标系。

这种结果可以用所谓伽利略相对性原理来表达：假使力学定律在一个坐标系中是有效的，那么在任何其他相对于这个坐标系做匀速直线运动的坐标系中也是有效的。

假使有两个坐标系，相互做不等速运动，则力学定律不会在两者之中都是有效的。“好的”坐标系就是力学定律在其中有效的坐标系，被称为惯性系。究竟是否存在一个惯性系的问题，直到现在还无法确定。但是如果有一个这样的系统，便会有无数个这样的系统。凡是对第一个惯性系做匀速直线运动的坐标系都是惯性坐标系。

我们来研究这样一个例子：有两个坐标系从已知的某一点出发，而且以已知速度相对做匀速直线运动。假如有人喜欢做具体的构思，他可以想到一艘船或是一列火车相对于地面在运动。力学定律可以在地面上，也可以在与它做匀速直线运动的火车内或船上以同样精确度的实验加以确认。但是假如两个系统的观察者从他们各自不同系统的观点对同一事件进行观察而开始讨论时，便会产生某些困难。每一个人都想把别人的观察翻译成为自己的语言。再举一个简单的例子：从两个坐标系（一为地球，一为做匀速直线运动的一列火车）观察同一个质点的运动。这两个坐标系都是惯性的。如果两个坐标系在某个时刻的相对速度与相对位置都是已知的，那么是否知道一个坐标系中的观察结果，便可以求出另一个坐标系中的观察结果呢？要描述自然现象，我们必须知道从一个坐标系过渡到另一个坐标系的方法，这是非常重要的，因为这两个坐标系是等效的，所以同样适宜于描写自然界中的现象。事实上，只要知道在一个坐标系中的一个观察者所得到的结果，便可以知道在另一个坐标系中的观察者所得到的结果。

我们现在不用船或火车，而更抽象地来考虑这个问题。为简便起见，我们只研究直线运动。有一根坚硬的刻有标度的杆和一只好的钟。在简单的直线运动的情形中，这根坚硬的杆代表一个坐标系，正如伽利略的实验中的塔上的标度尺一样。在直线运动的情形中，把一个坐标系想象为一根坚硬的杆，在空间中的任意运动的情形中，把一个坐标系想象为一个由相互平行和相互垂直的杆构成的坚硬的框架，而不管什么塔、墙、街道以及其他这一类的东西总是比较简单些、好些。假设在这里的最简单的情形中，有两个坐标系，就是说，有两根坚硬的杆；假定一根杆放在另一根杆上面，我们分别称它们为“上面的”和“下面的”坐标系。我们假定这两个坐标系以一定的速度相对运动，一根杆沿着另一根滑动。为妥当起见，再假定两根杆是无限长的，只有起点而没有终点。这两个坐标系只用一只钟就够了，因为时间的流逝对这两个坐标系是一样的。在观察开始的时候，两根杆的起点是重合的。这个时候，一个质点的位置在两个坐标系中都是用同一个数字来表示的。这个质点的位置跟杆的刻度上的某一点是重合的，这样我们就得到决定这个质点的位置的数字。但是假如两根杆相对做匀速运动，在运动了一段时间以后（譬如说一秒钟之后），表示位置的数字就各不相同了。试看图52中，静止在上面的杆上的一个质点，在上面的坐标系中决定它的位置的数字并不随时间而改变，但是在下面的杆上的相应数字却是随时间而改变的。我们不说“对应于质点的位置的数字”，而常常简单地说成“质点的坐标”。虽然后面这句话听来似乎很深奥，但从图上看来却是正确的，而且它所表示的意思是极简单的。质点在下面的坐标系中的坐标等于它在上面的坐标系中的坐标加上上面的坐标系的起点坐落在下面的坐标系中的坐标。重要的是，假如我们知道质点在一个坐标系中的位置，便能计算它在另一个坐标系中的位置。为此，我们必须知道在每个时刻这两个坐标系的相对位置。其实上面这些话，是很简单的，如果不是因为后面要用它，还不值得做这样详细的讨论。(https://www.xing528.com)

这里我们要注意一下决定一个质点的位置和决定一个事件的时间的差别。每一个观察者都有他自己的杆作为他的坐标系，但是他们却共用一只钟。时间有点像“绝对的”，它对于所有坐标系中的所有观察者都是同样流逝的。

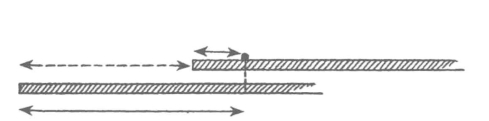
图52

现在再举一个例子。有一个人以每小时3英里的速度在一艘大船的甲板上散步。这是他相对于船的速度，或者换句话说，是他相对于严密地关联于船的坐标系的速度。假使船相对于岸的速度是每小时30英里，而人与船的匀速直线运动的方向又相同，则这个散步的人，相对于一个岸上的观察者的速度是每小时33英里，或者相对于船是每小时3英里。我们可以把这种情况说得更抽象一些：一个质点相对于下面的坐标系的速度，等于它相对于上面的坐标系的速度，加上或减去（究竟是加或减，得看速度的方向是相同还是相反）上面的坐标系相对于下面的坐标系的速度（图53）。因此假如我们知道两个坐标系的相对速度，就不仅可以把一个坐标系的位置转换到另一个坐标系的位置，而且可以把一个坐标系的速度转换到另一个坐标系的速度。位置或坐标以及速度是在不同的坐标系中便不相同的几种量，然而都是以某种（在这个例子中是很简单的）转换定律联系起来。

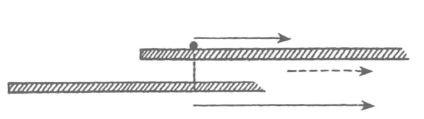
图53

可是有些量在两个坐标系中都是相同的，所以它们用不到转换定律。例如在上面的杆上不是取定一点而是取定两点，并考察它们之间的距离。这个距离便是两点的坐标之差。为了要找出这两点对于不同的坐标系的位置，我们必须应用转换定律。但是在构图的过程中，两个位置之间的坐标之差由于不同坐标系所产生的影响已相互抵消了，这在图54中可以很明显地看到。我们得先加上，然后减去两个坐标系的起点之间的距离。因此两点之间的距离是不变的，也就是说它与坐标的选择无关。

另一个与坐标系无关的量的例子是速度的改变，这是我们在力学中已很熟悉的一个概念。假如从两个坐标系去观察一个沿直线运动的质点。对每一个坐标系中的观察者来说，它的速度的改变等于两个速度之差，而两个坐标之间的匀速相对运动所产生的影响在计算两者之差的过程中消去了。因此，速度的改变是一个不变量。但是有一个条件，即两个坐标系的相对运动必须是匀速直线的。不然，在每个坐标系中速度的改变也会不同，这种差异是由于代表我们的坐标系的两根杆的相对运动的速度改变所致。

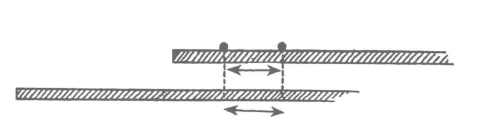
图54

现在举最后一个例子。设有两个质点，作用于其间的力只与距离有关。在匀速直线运动的情况下，距离是不变量，因而力也是不变量。因此把力和速度的改变联系起来的牛顿定律，在两个坐标系中都是有效的。我们又一次得到了一个为日常经验所确认的结论：假如力学定律在一个坐标系中是有效的，则它们在对应于这一个坐标系做匀速直线运动的一切坐标系中都是有效的。当然，我们的例子是很简单的，是一种直线运动的例子，其中的坐标系可以用一根坚硬的杆来表示。但是我们的结论大体上是普遍有效的，可以被概括为下列几条：

1.我们不知道有什么法则可以找出一个惯性系。可是，如果假定出一个来，我们便可以找到无数个。因为所有互相做匀速直线运动的坐标系，只要其中有一个是惯性系，则它们全部是惯性系。

2.与一个事件相对应的时间，在一切坐标系中都相同。但坐标与速度却都不相同，它们依照转换定律而变化。

3.虽然坐标与速度由一个坐标系过渡到另一个坐标系时是改变的，但是，力与速度的改变对于转换定律都是不变的，因而所有的力学定律对转换定律也是不变的。

我们把上面所表述的坐标与速度的转换定律称为经典力学的转换定律，或简称为经典转换。