分析应用：静力法影响线（MF影响线示例）

例如图6-2（a）所示多跨静定梁，图6-2（b）为其层叠图，现要作弯矩MF的影响线。当F=1在CE段上移动时，D′E段为ID′段的附属部分，只将力传递给ID′段，而ID′段作为主要部分并不会传力给HI段附属部分，故A′H不受力，故MF的影响线在CE段内的纵距恒为零；当F=1在A′H段上移动时，此时MF的影响线与A′H段单独作为伸臂梁时相同；当F=1在HI段上移动时，A′H梁则承受一个作用位置不变而大小变化的力FHY的作用。以H点为坐标原点，写出FHY的影响线方程为FHY =（2-x）2，可见，FHY是x的一次式。由这个反力所引起的A′H段梁内指定截面的内力也是x的一次式，如A′H段内是一直线。画出直线只需定出两点，当x=0时，MF=1/2；当x=l时，MF=0。MF影响线在全梁的变化图形如图6-2（d）所示。

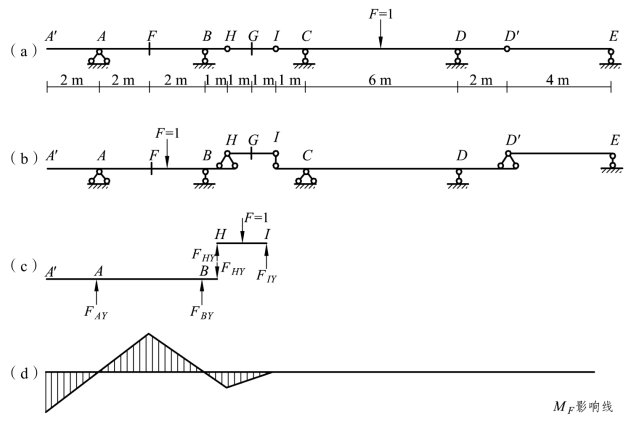
图6-2　静力法求解影响线过程

由上述分析可知，多跨静定梁反力及内力影响线的一般作法如下：(www.xing528.com)

（1）当F=1在所求量值所在的梁段上移动时，该量值的影响线与相应单跨静定梁影响线相同。

（2）当F=1在对于该量值所在的梁段来说是附属部分的梁段上移动时，量值的影响线是一直线，可根据支座处纵距为零，铰处的纵距为已知的两点绘出。

（3）当F=1在对于该量值所在的梁段来说是基本部分的梁段上移动时，该量值影响线的纵距为零。