结构分析有限元程序应用：平面单元模拟二维实体的应力和应变

平面单元用来模拟二维实体的平面应力和平面应变行为。

SAP2000中很多单元可以指定为非协调完全模式（对应程序单元定义中，选择不相容模式的复选框），包括平面单元、轴对称平面单元和实体单元。

在介绍非协调模式之前，先简单介绍一下剪力自锁现象。

考虑一个受纯弯曲结构中的一小块材料，材料将产生弯曲，如图3-15。平行于水平轴的直线按常曲率弯曲，而沿厚度方向上的直线保持为直线。水平线与竖直线之间的夹角为90°。

图3-15　弯曲材料的变形

一个线性单元的边不能弯曲，所以用单个单元来模拟小块材料，其变形后的形状如图3-16所示。

图3-16　线性单元变形

为清楚起见，图中画出了通过积分点的虚线。很明显，上面直线的长度增加，这说明1方向的应力11σ是拉伸的；类似的，下面直线的长度缩短，说明11σ是压缩的；数值直线的长度没有改变（假设位移很小），因此所有积分点上的22σ为零。所有这些结论与纯弯曲的小块材料的预测应力状态是一致的。但是在每一个积分点，竖直线与水平线之间的夹角开始时是90°，变形后改变了，这说明每一点的剪应力12σ不为零，这是不正确的；在纯弯曲下一块材料中的剪应力应为零。此现象即剪力自锁现象。(www.xing528.com)

引起剪力自锁现象的原因是单元的边不能弯曲。它的存在意味着应变能不引起弯曲变形而引起剪切变形。总挠度变小了，即单元太刚硬了。

剪力自锁只影响受弯曲荷载的弯曲积分线性单元，这些单元在受直接或剪切荷载时没有问题。

非协调模式可以用来解决完全积分一阶单元的剪力自锁问题。既然剪力自锁是由于单元的位移场不能模拟与弯曲相联系的运动学现象引起的，那么可把能够增强单元位移梯度的附加自由度引入到一阶单元，如图3-17。这种对位移梯度的增强，允许一阶单元中通过如图所示的单元范围的位移梯度有一个线性变化。标准的单元构造导致图中所示的单元范围的位移梯度有一个恒定的位移梯度，从而导致与剪应力自锁有关的非零剪应力。这种对位移梯度的增强对一个单元而言完全是内在的并且与单元边上的节点无关。

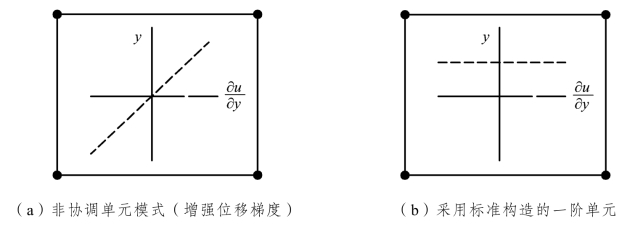
图3-17　非协调模式

在弯曲问题中，用非协调模式可以得到与二元单元相当的结果，应用非协调单元得当，则在很低花费时仍可得到很高精度，但必须保证单元扭转是非常小的，因为它对单元扭转十分敏感，因此当网格复杂时这一点是很难保证的。在弯曲不重要的情况下，如一般的岩土问题，则不能使用非协调弯曲模式。

平面单元在每一连接的节点激活了3个平动自由度，不激活转动自由度，平面应力单元只对单元面内的自由度贡献刚度，所以有必要对垂直于平面的平动自由度提供约束或其他支座；否则结构将不稳定。除平面行为外，平面应变单元模拟抵抗平面剪力，即剪力垂直于单元平面，这样就对所有3个自由度建立了刚度。

由平面单元质量贡献的质量集中在单元节点上，在单元内部不考虑惯性力。单元总质量等于在单元平面上对质量密度m乘以厚度t的积分，总质量用一致质量矩阵的对角元按比例分配给节点，总质量被分配给每个自由度UX、UY和UZ。对于转动角度，不计自重荷载激发模型中所有单元的自重。

平面单元可以承受自重荷载、表面及孔隙压力荷载和温度荷载。程序在平面单元的标准2×2高斯积分点计算应力，且向外插值到节点。